主成分分析(上篇)

1. 主成分分析基础知识准备

1.1 样本均值

    给定数据集\(D=\{x_1, x_2, ..., x_n\}\), 样本\(x_i\)是\(d\)维向量，则样本均值为

\[\overline{x}=\frac{x_1+x_2+...+x_n}{n}\tag{1} \]

    例1 给定一个数据矩阵

\[D_{3\times2}= \begin{bmatrix} 4 & 2\\ -1 & 2\\ 3 & 2 \end{bmatrix}\\ \]

    求样本平均？

\[x_1 = (4, 2)^T\\ x_2 = (-1, 2)^T\\ x_3 = (3, 2)^T \]

\[\overline{x}=\frac{x_1+x_2+x_3}{3}=(2, 2)^T \]

1.2 向量投影

1.2.1 两个维度的向量投影

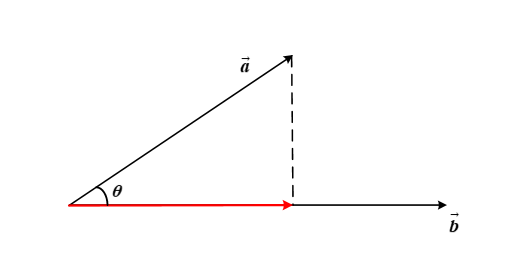
    求向量\(\vec{a}\)在向量\(\vec{b}\)上的投影，即红色线段的长度？

\[\lVert{\vec{a}}\rVert{cos{\theta}}=\lVert{\vec{a}}\rVert{\frac{\vec{b}^T.\vec{a}}{\lVert{\vec{a}}\rVert\lVert{\vec{b}}\rVert}}\\ =\vec{e}^T\vec{a}\tag{2} \]

1.2.2 三个维度的向量投影

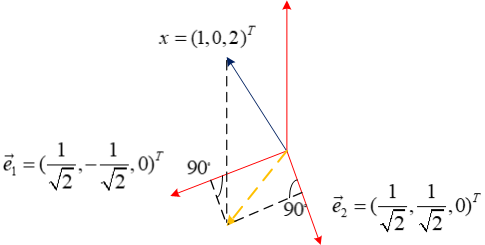
\[\vec{e_1}^T\vec{x}=(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},0)\begin{pmatrix}1\\0\\2\end{pmatrix}=\frac{1}{\sqrt{2}}\\ \vec{e_2}^T\vec{x}=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0)\begin{pmatrix}1\\0\\2\end{pmatrix}=\frac{1}{\sqrt{2}} \]

则，投影的向量坐标为\((\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})^T\).它的矩阵形式如下：

\[\begin{bmatrix} \vec{e_1}^T\\ \vec{e_2}^T \end{bmatrix}x = \begin{bmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0\\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \end{bmatrix} \begin{bmatrix} 1\\ 0\\ 2 \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{bmatrix} \]

这就是一个线性变换，将三维向量映射为二维向量。

1.3 矩阵微分

    在向量空间上定义函数\(f\)，即\(f:R^d\rightarrow{R}\),那么函数对向量的微分形式为:

\[\frac{\partial f}{\partial \vec{x}}= \begin{bmatrix} \frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\\ \vdots\\ \frac{\partial f}{\partial x_d} \end{bmatrix}\tag{3} \]

    例2 令向量\(\vec{w}=(w_1,w_2,w_3)^T\),函数\(g(\vec{x})=2w_1+5w_2+12w_3=(2,5,12)\vec{w}\),则

\[\frac{\partial g}{\partial \vec{w}}= \begin{bmatrix} \frac{\partial g}{\partial w_1}\\ \frac{\partial g}{\partial w_2}\\ \frac{\partial g}{\partial w_3}\\ \end{bmatrix} = \begin{bmatrix} 2\\ 5\\ 12\\ \end{bmatrix} \]

    例3 对下面函数求导：

\[f(\vec{e})=e_1^2+e_2^2+\cdots+e_d^2=\vec{e}^T\vec{e}\tag{4} \]

解：

\[\frac{\partial \vec{e}^T\vec{e}}{\partial \vec{e}} = \begin{bmatrix} \frac{\partial \vec{e}^T\vec{e}}{\partial e_1}\\ \frac{\partial \vec{e}^T\vec{e}}{\partial e_2}\\ \vdots\\ \frac{\partial \vec{e}^T\vec{e}}{\partial e_d}\\ \end{bmatrix} = 2\begin{bmatrix} e_1\\ e_2\\ \vdots\\ e_d\\ \end{bmatrix} \]

    例4

\[A= \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1d}\\ a_{21} & a_{22} & \cdots & a_{2d}\\ \vdots & \vdots & \ddots & \vdots\\ a_{d1} & a_{d2} & \cdots & a_{dd}\\ \end{bmatrix} \]

求\(\frac{\partial \vec{e}^TA\vec{e}}{\vec{e}}\)
解：
当

\[A= \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} \]

时，

\[\vec{e}^TA\vec{e}= \begin{bmatrix} e_1 & e_2 \end{bmatrix} \begin{bmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} e_1 \\ e_2 \end{bmatrix}\\ = \begin{bmatrix} e_1a_{11}+e_2a_{21} & e_1a_{12}+e_2a_{22} \end{bmatrix} \begin{bmatrix} e_1 \\ e_2 \end{bmatrix}\\ = e_1^2a_{11}+e_2e_1a_{21}+e_1e_2a_{12}+e_2^2a_{22} \]

则，

\[\frac{\partial \vec{e}^TA\vec{e}}{\vec{e}}= \begin{bmatrix} 2a_{11}e_1 + (a_{12}+a_{21})e_2\\ (a_{21}+a_{12})e_1 + 2a_{11}e_2 \end{bmatrix}\\ = (A+A^T) \begin{bmatrix} e_1 \\ e_2 \end{bmatrix}\\ \]

所以，当矩阵为\(n\times{n}\)时，

\[\frac{\partial \vec{e}^TA\vec{e}}{\vec{e}}=(A+A^T)\vec{e}\tag{5} \]

特殊情况，当\(A\)对称矩阵，即\(A=A^T\)

\[\frac{\partial \vec{e}^TA\vec{e}}{\vec{e}}=2A\vec{e}\tag{6} \]