花授粉优化算法-python/matlab

import numpy as np
from matplotlib import pyplot as plt
import random

# 初始化种群
def init(n_pop, lb, ub, nd):
    """
    :param n_pop: 种群                                                                                  
    :param lb: 下界
    :param ub: 上界
    :param nd: 维数
    """
    p = lb + (ub - lb) * np.random.rand(n_pop, nd)
    return p


# 适应度函数
def sphere(x):
    y = np.sum(x ** 2, 1)
    return y


f_score = sphere  # 函数句柄


# Levy飞行Beale
def Levy(nd, beta=1.5):
    num = np.random.gamma(1 + beta) * np.sin(np.pi * beta / 2)
    den = np.random.gamma((1 + beta) / 2) * beta * 2 ** ((beta - 1) / 2)
    sigma_u = (num / den) ** (1 / beta)

    u = np.random.normal(0, sigma_u ** 2, (1, nd))
    v = np.random.normal(0, 1, (1, nd))

    z = u / (np.abs(v) ** (1 / beta))
    return z


def FPA(Max_g, n_pop, Pop, nd, lb, ub, detail):  # FPA算法
    """
    :param Max_g: 迭代次数
    :param n_pop: 种群数目
    :param Pop: 花粉配子
    :param nd: 维数
    :param lb: 下界
    :param ub: 上界
    :param detail: 显示详细信息
    """
    # 计算初始种群中最好个体适应度值
    pop_score = f_score(Pop)
    g_best = np.min(pop_score)
    g_best_loc = np.argmin(pop_score)
    g_best_p = Pop[g_best_loc, :].copy()

    # 问题设置
    p = 0.8
    best_fit = np.empty((Max_g,))
    # 迭代
    for it in range(1, Max_g + 1):
        for i in range(n_pop):
            if np.random.rand() < p:
                new_pop = Pop[i, :] + Levy(nd) * (g_best_p - Pop[i, :])
                new_pop = np.clip(new_pop, lb, ub)  # 越界处理
            else:
                idx = random.sample(list(range(n_pop)), 2)
                new_pop = Pop[i, :] + np.random.rand() * (Pop[idx[1], :] - Pop[idx[0], :])
                new_pop = np.clip(new_pop, lb, ub)  # 越界处理
            if f_score(new_pop.reshape((1, -1))) < f_score(Pop[i, :].reshape((1, -1))):
                Pop[i, :] = new_pop
                # 计算更新后种群中最好个体适应度值
        pop_score = f_score(Pop)
        new_g_best = np.min(pop_score)
        new_g_best_loc = np.argmin(pop_score)

        if new_g_best < g_best:
            g_best = new_g_best
            g_best_p = Pop[new_g_best_loc, :].copy()
        best_fit[it - 1] = g_best

        if detail:
            print("----------------{}/{}--------------".format(it, Max_g))
            print(g_best)
            print(g_best_p)

    return best_fit, g_best


if __name__ == "__main__":
    pop = init(30, -100, 100, 2)
    fitness, g_best = FPA(1000, 30, pop, 2, -100, 100, True)

    # 可视化
    plt.figure()
    # plt.plot(fitness)
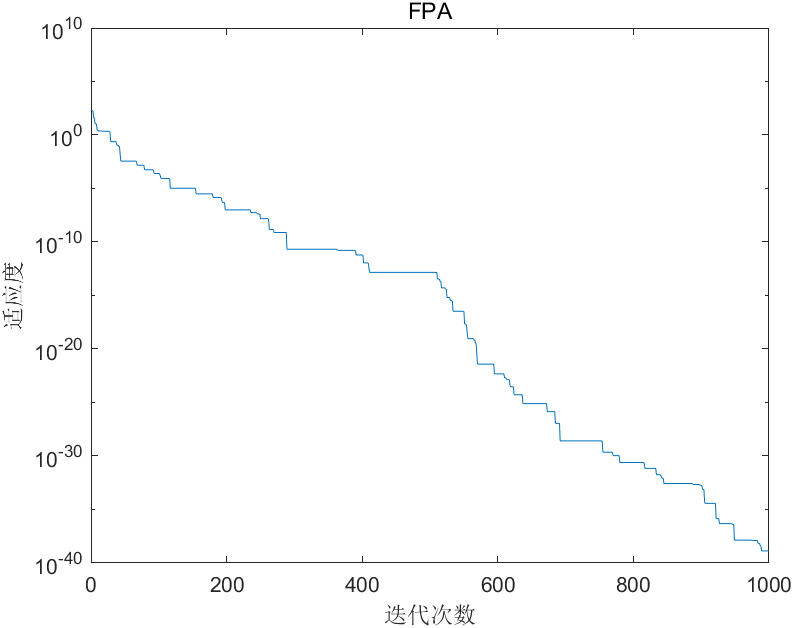
    plt.semilogy(fitness)
    # 可视化
    # fig = plt.figure()
    # plt.plot(p1, fit)
    plt.show()

import numpy as np
from matplotlib import pyplot as plt

plt.style.use('ggplot')

plt.rcParams["font.sans-serif"] = ["Microsoft YaHei"]
plt.rcParams["axes.unicode_minus"] = False


def sphere(x):
    y = 0
    for e in x.flatten():
        y += e ** 2
    return y


class FPA:
    def __init__(self, num_pop, dim, ub, lb, f_obj, verbose):
        self.num_pop = num_pop  # 种群数目
        self.dim = dim  # 维数
        self.ub = ub  # 上界
        self.lb = lb  # 下界
        self.pop = np.empty((num_pop, dim))  # 种群
        self.f_obj = f_obj  # 目标函数
        self.f_score = np.empty((num_pop, 1))
        self.verbose = verbose  # 显示

        self.p_best = None  # 最好个体
        self.f_best = None  # 最好适应度值

        self.iter_f_score = []

    def initialize(self):
        """
        种群初始化
        :return: 初始化种群和种群分数
        """
        for i in range(self.num_pop):
            self.pop[i, :] = self.lb + (self.ub - self.lb) * np.random.rand(1, self.dim).flatten()
            self.f_score[i] = self.f_obj(self.pop[i, :])
        return [self.pop, self.f_score]

    def get_best(self):
        """
        获取最优解
        :return: 最优索引和最优得分
        """
        idx = np.argmin(self.f_score)
        self.p_best = self.pop[idx, :]
        self.f_best = np.min(self.f_score)
        return [self.p_best, self.f_best]

    def Levy(self, beta=1.5):
        """
        莱维飞行
        :param beta: 固定参数
        :return: 随机数
        """
        sigma = (np.random.gamma(1 + beta) * np.sin(np.pi * beta / 2) / (
                np.random.gamma((1 + beta) / 2) * beta * 2 ** ((beta - 1) / 2))) ** (1 / beta)
        # print(sigma)
        u = np.random.normal(0, sigma, (1, self.dim))
        v = np.random.normal(0, 1, (1, self.dim))
        levy = u / (np.abs(v) ** (1 / beta))
        return levy

    def fit(self, max_generation, p=0.8):
        """
        算法迭代
        :param max_generation: 最大迭代次数
        :param p: 切换概率
        :return: 最优值和最优个体
        """
        self.pop, self.f_score = self.initialize()  # 初始化
        self.p_best, self.f_best = self.get_best()  # 当前最优个体

        self.iter_f_score.append(self.f_best)

        # 迭代
        for i in range(max_generation):
            for j in range(self.num_pop):
                if np.random.rand() < p:
                    # 异花授粉公式
                    new_pop = self.pop[j, :] + self.Levy() * (self.pop[j, :] - self.p_best)
                else:
                    # 自花授粉公式
                    idx_set = np.random.choice(range(self.num_pop), 2)
                    new_pop = self.pop[j, :] + np.random.rand(1, self.dim) * (self.pop[idx_set[0], :] -
                                                                              self.pop[idx_set[1], :])

                # 越界处理
                new_pop = np.clip(new_pop.flatten(), self.lb, self.ub)
                new_f_score = self.f_obj(new_pop)

                # 进化算法
                if new_f_score < self.f_score[j]:
                    self.pop[j, :] = new_pop
                    self.f_score[j] = new_f_score

                if new_f_score < self.f_best:
                    self.p_best = new_pop
                    self.f_best = new_f_score

            self.iter_f_score.append(self.f_best)

            if self.verbose:
                print("============{}/{}==============".format(i, max_generation))
                print(self.f_best)

        return [self.iter_f_score, self.f_best]


# 测试
if __name__ == "__main__":
    n_pop = 20
    d = 2
    upper = 100
    lower = -100

    max_iter = 1000

    fpa = FPA(n_pop, d, upper, lower, sphere, True)
    iter_score, _ = fpa.fit(max_iter)

    xx = [int(i) for i in range(0, 1001, 50)]
    yy = np.array(iter_score)

    plt.figure()
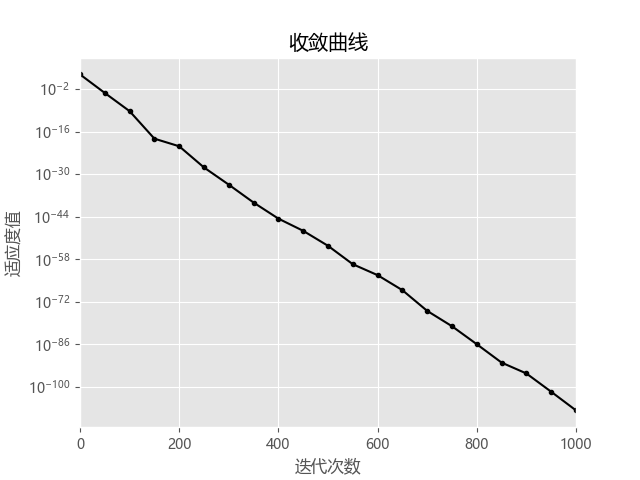
    plt.title("收敛曲线")
    plt.semilogy(xx, yy[xx], c='k', marker='.')
    plt.xlim([0, 1000])
    plt.xlabel("迭代次数")
    plt.ylabel("适应度值")
    plt.show()

 

花授粉算法Matlab代码
% 清屏和工作空间变量
clc
clear
Step 1:    问题定义
npop = 30;    % 种群数目
dpop = 2;     % 种群维数
ub = 100;     % 种群的上界
lb = -100;    % 种群的下界
Step 2： 初始化种群  
pop = lb + rand(npop, dpop).*(ub - lb);  % pop是初始种群
Step 3：适应度函数 
fScore = @ sphere
Step 4：Levy飞行
levy = @ Levy
Step 5：计算初始种群最好的适应度值
popScore = fScore(pop);
[bestscore, loc] = min(popScore);
bestpop = pop(loc, :);
Step 6：参数设置
iterMax = 1000;  %  最大迭代次数
p = 0.8;  %  转换概率
BestScore = ones(iterMax, 1);
Step 7：越界处理
Clip = @ clip;  % 越界处理函数
Step 8：迭代
for it=1:iterMax
    for i = 1:npop
        if rand < p
            newpop = pop(i, :) + levy(1, dpop).*(bestpop - pop(i, :));  % 异花授粉
        else
            idx = randsample(30, 2);
            newpop = pop(i, :) + rand*(pop(idx(1), :) - pop(idx(2), :));  % 自花授粉
        end
        newpop = Clip(newpop, ub, lb);  % 越界处理
        if fScore(newpop) < fScore(pop(i, :))
            pop(i, :) = newpop;  % 更新种群
        end
    end
    popScore = fScore(pop);
    [newBestScore, Loc] = min(popScore);
    if newBestScore < bestscore
        bestscore = newBestScore;
        bestpop = pop(loc, :);
    end
    BestScore(it) = bestscore;
    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(bestscore)]);
    disp(['Bestpop ' num2str(bestpop)])
end
Step 9：可视化
figure
semilogy(BestScore)
% plot(BestScore)
xlim([0 1000])
xlabel('迭代次数')
ylabel('适应度')
title('FPA')

function L=Levy(d)
%% Levy飞行
    beta=3/2;
    sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
    u=random('normal', 0, sigma, 1, d);
    v=random('normal', 0, 1, 1, d);
    L=0.01*u./abs(v).^(1/beta);
end

function s=simplebounds(s,Lb,Ub)
%% 越界处理函数
    ns_tmp=s;
    I=ns_tmp<Lb;
    ns_tmp(I)=Lb(I);
    J=ns_tmp>Ub;
    ns_tmp(J)=Ub(J);
    s=ns_tmp;
end

function [y] = Sphere(xx)
%% 目标函数
    d = length(xx);
    sum = 0;
    for ii = 1:d
        xi = xx(ii);
        sum = sum + xi^2;
    end

    y = sum;
end