VSLAM 十四讲--阅读中知识点记录
1. 前言
砚上三五笔,落墨鹧鸪啼
本文用于记录:VSLAM相关。
PS:笔者梦到哪里写哪里,毫无逻辑可言。。。
如有不对,欢迎评论区指正!
2. 正文
2.1 SLAM
-
simultaneous location and mapping
同步定位和建图 -
相机:单目相机,双目相机成像(两只眼睛的视差),RGB-D深度相机,获得深度信息。
-
整体框架。
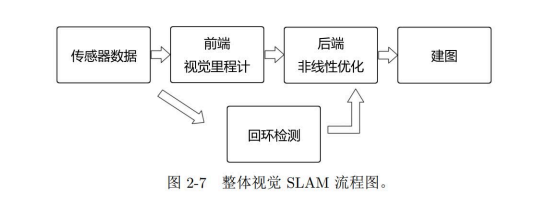
1.传感器信息读取。
2.前端 (视觉里程计 Visual Odometry)。视觉里程计主要估算相邻图像间的相机运动,以及局部地图的样子。只计算相邻时刻的运动。但这样会导致累计偏移。因为误差是通过前后两帧进行累加的。。。Drift。

3.后端优化。主要处理SLAM过程中噪声的问题。最大后验估计。不管数据来自哪里,只去负责优化这些数据等。

空间状态不确定性估计。是早期后端要解决的问题。对运动主题自身和周围环境的不确定性估计。
4.回环检测、闭环检测。检测是否到达过之前的位置。辨认来自同一个地方,可显著降低累积误差 。视觉回环检测实际上是一种计算图像数据相似性算法。
5.建图。一组空间点的集合可以叫做地图。

-
度量地图(Metric Map)。精确性。sparse和dense。sparse主要包括landmark路标进行标志性建图;dense地图着重强调每一处细节。其中稠密地图又分为二维网格pixel和三维体素网格voxel。建图数据可以用来应用各种导航算法,比如A,D等。但是往往需要耗费较大的磁盘空间去存储。
-
拓扑地图(Topological Map)。抽象性。强调地图元素之间的关系。是一个图Graph。由节点和边组成,只考虑节点之间的可达性和连通性。
-
数学描述。运动方程和观测方程。将SLAM问题建模为一个状态估计的问题。位姿:位置加姿态。


-
状态估计问题的求解。线性\非线性系统;高斯\非高斯系统。

2.* linux上的cpp编译基础等
这部分一些人只会cmake或者只知其然二不知其所以然,所以这里做一下简单的额补充。
-
可执行文件类型。

-
g++
在新建文件当前目录执行g++,这个是一个C++编译器,编译为一个可执行文件,如a.out,我们在控制台执行./a.out,输出。 -
cmake和make
程序规模过大,一个一个文件的g++不太现实。用cmake进行批量编译。使用CMakeList.txt来告诉cmake对这个目录做什么。在一个cmake工程中,使用cmake生成makefile文件,使用makefile文件和make命令来编译整个工程。
makefile是一个自动编译化脚本
mkdir build
cd build
cmake ..
make
- 静态库和共享库。静态库.a,共享库.so,所有库都是一些函数打包后的集合。静态库每次被调用后都生成一个副本,而共享库只有一个副本,更节省空间。

代码写法:

这里推荐使用opencv库的下载和链接方式来仔细学习下在Linux下的代码编写原则。弄的清楚些。。有两种方式:
主要配置方法和说明 如下:
# 寻找OpenCV库
find_package(OpenCV REQUIRED)
# 添加头文件
include_directories(${OpenCV_INCLUDE_DIRS})
# 链接OpenCV库 xxx为可执行文件的名字
target_link_libraries(xxx
${OpenCV_LIBS}
)
2.2 旋转&四元数
1.
- 内积(点乘)和外积(叉乘)
- 相机运动为刚体运动
- 旋转矩阵,行列式为1(作用于向量时不会产生伸缩变化)的正交矩阵(转置等于其矩阵的逆)
- Speicial Orthogonal Group 特殊正交群,SO(3)表示三维空间的正交基地下的旋转。
2.
- 数学技巧,齐次坐标(这里的齐次表示对齐次幂),新增加这一维度是为了对齐旋转矩阵,因为旋转矩阵一般为方阵,需要维度对应。

- Special Euclidean Group SE()特殊欧式群。由旋转SO(3)和平移R3组成的一个矩阵

- Eigen C++库,矩阵运算
3.
- 任意旋转都可以用轴+角表示。旋转向量:方向与旋转轴一致,向量的模长为旋转角大小。

- 罗德里格斯公式:旋转向量-->旋转矩阵
从性质中不难发现,旋转矩阵的特征值为1对应的特征特征向量,为旋转轴。(不改变旋转向量前后的长度,只改变方向。) - 欧拉角
yaw |偏航角 |绕z轴
roll |滚转角 | 绕x轴
pitch |俯仰角 | 绕y轴
(这里采用的是右手系) - 欧拉角产生万向锁的问题(Gimbal Lock)。当俯仰角为土90度时,两个旋转轴会重合,这样整个系统就会丢失一个自由度。奇异值问题。欧拉角不适合插值和迭代,寻找替代方案。。。

(个人认为这个经纬度的例子很直观)
-
四元数。(Quaternion),解决了奇异值的问题。

-
虚四元数(实部为0,对应三维空间中的点)
-
单位复数能表示二维平面的旋转,那么单位四元数能表示空间中的旋转。
-
任意旋转都可以由两个互为相反数的四元数表示。
-
不表示任何旋转的四元数,一般在代码中用来初始化:

-
轴角转四元数。感觉像转了角度的一半一样。这么看来感觉轴角转成四元数更直观些啊。。

-
性质:
1.加减

2.乘法。因此从外积的公式可以看到四元数的乘法是不满足交换律的。
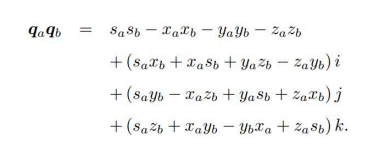
整理一下:

3.共轭。
\(q\cdot \bar{q} = ||q||^2\)
4.模长

5.逆。单位四元数的共轭为其逆

6.点乘。和向量一样。
7.q=-q,表示同一种旋转。
可以从轴角表示的式子简单推出。cos函数内的角度用pi减,表示互补,sin函数的角度取相反数。从几何角度不难看出向量和原来是共线的。
- 用四元数表示旋转。这里直接粘贴原书中的内容。

- 变换
1.欧拉变换 :旋转平移不伸缩原始向量
2.相似变换:多了一个缩放系数,边长为1的立方体变为边长为10的立方体,立方体还是立方体,但体积变化了。

矩阵的相似变换,
3.仿射变换,保持几何性质的不变性,如正方形-->平行四边形,圆形-->椭圆形。相机焦距无限远的情况下。
4.射影变换,从真实世界到相机图像的变换是一种射影变换。
四元数旋转某个三维空间中的点,得到的依然是一个虚四元数。
2.3 李群和李代数
- 为什么用它?一般的旋转矩阵带自约束的,比如行列式为1,正交矩阵,但是实际优化过程中引入额外的约束会使得优化变得很困难。

- SO(3)【特殊正交变换】表征旋转矩阵(3维空间下)和SE(3)【特殊欧式变换】表征变换矩阵(旋转加平移,3维空间下)

- 对加法不封闭。对乘法封闭。

- 群(Group)。一种代数结构,通常是一个集合加上一种运算。

- 李群。连续光滑性质的群。对比整数的离散群,旋转群是连续的。主要讨论SO(3)和SE(3)两个李群。
简单举个例子,这个矩阵是李群SO(3)中的一个元素
- 李代数。这个是怎么来的,先来简单推导下:


个人理解:一个旋转矩阵可以表示为一个三维向量的反对称矩阵的指数的形式,这个三维向量组成了李代数集合。
- 李代数so(3)。

- 李代数se(3)。

指数的性质不难看到,矩阵的乘法运算可以间接转化为李代数的加法运算。根据指数的性质不难看到,矩阵的乘法运算可以间接转化为李代数的加法运算。
- 李群和李代数的转换。由于推导过于复杂,笔者也不想仔细研究了,所以读者可以自行阅读原著。指对数映射。
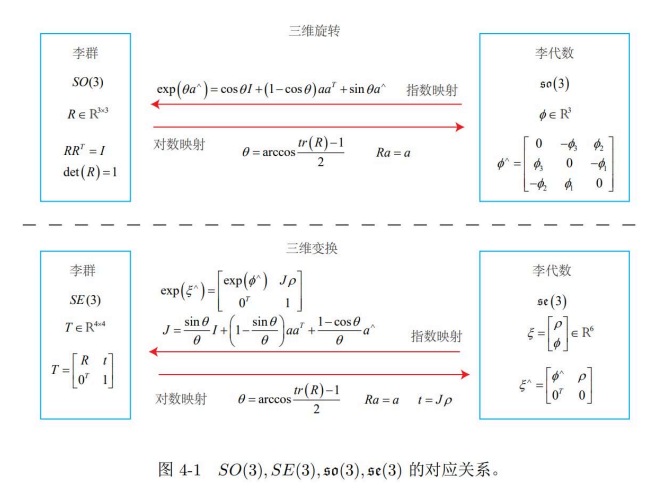
- 李群李代数求导(略)。
2.4 相机模型
-
三维空间投影到二维空间中。畸变,相机镜头透镜,使得光线投影产生畸变。
-
内参数。针孔模型 + 畸变模型。
-
从镜像原点的坐标系下(X,Y,Z)转换到像素坐标系(左上原点为[0,0],横轴x,纵轴为y)。中间的带f...矩阵为内参数矩阵。
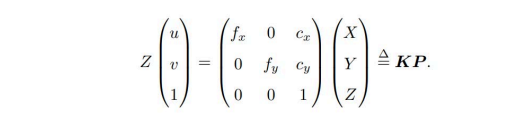
-
外参数。相机的旋转 角度和位置偏移。
-
畸变。为了更好的实现成像的效果,常加入透镜,会导致成像产生一些影响:

-
单目相机成像原理:

-
双目相机成像原理:景深。
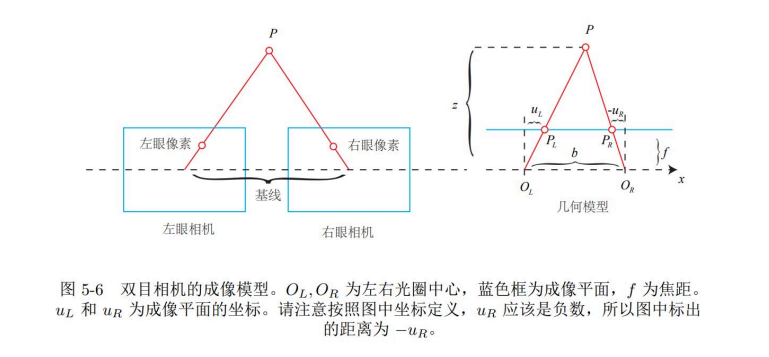
这里的d为左右两个图的对应的横坐标之差,被称为“视差”。经推导,视差和成像距离是成反比的,当两个视差区域0,也就是单目相机的话,那么成像是看不到深度的,是不是也就从双目相机进化到了单目相机。
但视差d的计算比较复杂,所以深度估计通常需要GPU或者FPGA等进行计算。

- RGBD相机模型原理。主动。
发射器和接收器。
1.红外结构光。structured light。发送红外结构光,接收红外结构光。根据结构光的图案变化。。。
2.飞行时间。time of flight。 发送脉冲,接收脉冲。计算时间差。
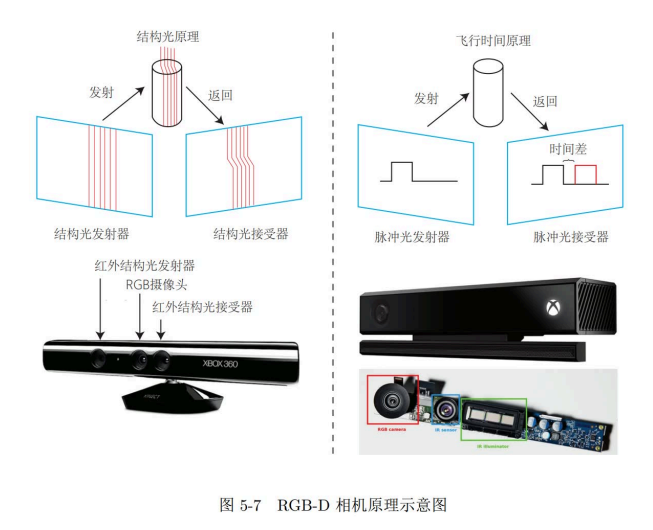
根据rgb相机的色彩信息和深度相机的位置信息,计算出像素的3D相机坐标 ,生成点云。

以后说存储空间也行,但是说磁盘空间比较好,比内存的要严谨些。😃
- 计算机中图像表示。灰度8bit,1字节。OpenCV的默认是BGR,但是这都无所谓其实,24个比特。
2.5 非线性优化
-
方程。x为状态,z观测值,u为输入值(传感器输入)。

-
贝叶斯法则:先验和后验。
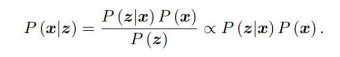
贝叶斯公式的左侧是后验概率(已知观测求状态概率),右侧为似然和先验概率。似然描述为“在现在的状态x下最可能产生什么样子的观测数据z”,如果已知观测数据,就是最大似然估计,理解为:在什么状态x下,最可能产生现在的观测到的数据

- 非线性最小二乘。
对于优化问题:要如何求解。
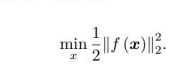
如果f的形式很简单的话,我们其实是可以直接求出其数值解的。但如果函数过于复杂,我们其实可以采用迭代的形式进行最优值的求解运算。
- 一阶二阶梯度法。泰勒展开。
- G-N法
2.6 视觉里程计VO
- 提取ORB 提取特征点 SIFT FAST。
- 特征点匹配。hamming距离:等长字符串在对应位置上不同字符的个数。

- 2D-2D 对极几何。求解相机的运动 R t。
- 3D-2D PnP。双目相机的方案中,直接用RGB-D相机确定特征点的3D位置,
- 光流。像素在图像中的移动。
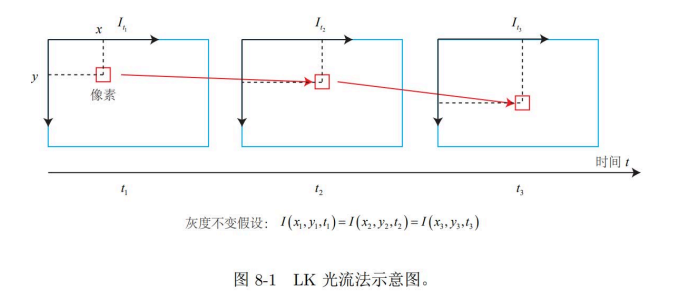
- 直接法。通过第一二帧的位置根据描述的同一物体的3维坐标描述空间中的旋转。
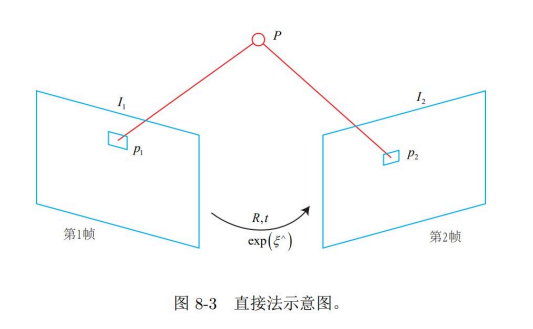
3. 后记
To be continued.......


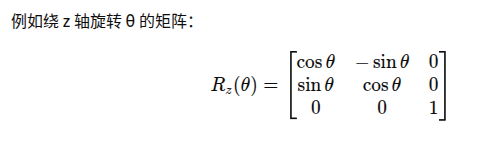

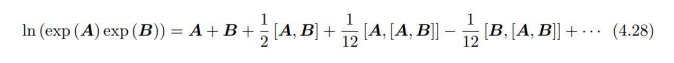



 浙公网安备 33010602011771号
浙公网安备 33010602011771号