CSP初赛复习-26-贪心算法

贪心算法

所谓贪心算法是指，在对问题求解时，总是做出在当前看来是最好的选择 。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的 局部最优解

每一个贪心算法之下，几乎总有一个更加繁琐的动态规划算法

两个重要因素

贪心选择性

可以通过做出局部最优（贪心）选择来构造全局最优解

对于一个具体问题，要确定它是否具有贪心选择性质，我们必须证明每一步所作的贪心选择最终导致问题的一个整体最优解

最优子结构

当一个问题的最优解包含着它的子问题的最优解时，称此问题具有最优子结构性质

也可以认为如果对每个子问题的最优解可以构建全局最优解，说明具有最优子结构

例题1 找零钱问题

某商店不能电子支付，钱柜里的货币只有 25 分、10 分、5 分和 1 分四种硬币，如果你是售货员且要找给客户 41 分钱的硬币，如何安排才能找给客人的钱既正确且硬币的个数又最少？

分析

贪心选择性

钱币保证最大面额大于其他小于它的面额之和，保证了每次选择最大的没有其他优于这个组合

即 选择了25 即使选择10+5+1=16都比25小

每次选择找零面额最大的,每次都是本次最优(局部最优)，根据钱币面额本身的性质可知，可以保证全局最优

最优子结构

此问题可以拆分4个子问题，每个子问题产生一个解，分别是25，10，5，1保证找零正确的情况下，找零硬币个数最少

4个子问题是局部最优解，每个子问题最优解组成了全局最优解，因此称为最优子结构

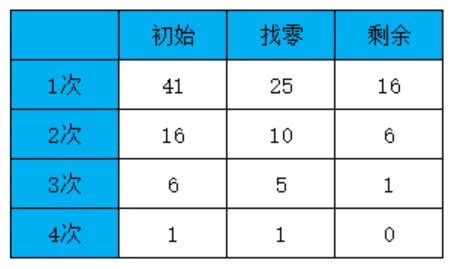
因此，总找零41分通过以下步骤，按硬币面额大的先找零贪心策略找零，如下

1 先找零25

2 再找零10

3 再找零5

4 再找零 1

参考程序

#include<bits/stdc++.h>
using namespace std;
int main() {
    int n;
    cin >> n;
    int n25 = n / 25;
    n -= 25 * n25;
    int n10 = n / 10;
    n -= 10 * n10;
    int n5 = n / 5;
    n -= 5 * n5;
    cout << "\n1分硬币个数:\t" << n
              << "\n5分硬币个数:\t" << n5
              << "\n10分硬币个数:\t" << n10
              << "\n25分硬币个数:\t" << n25;
    return 0;
}
/*
输入: 
41
输出： 
1分硬币个数:    1
5分硬币个数:    1
10分硬币个数:   1
25分硬币个数:   1
*/ 

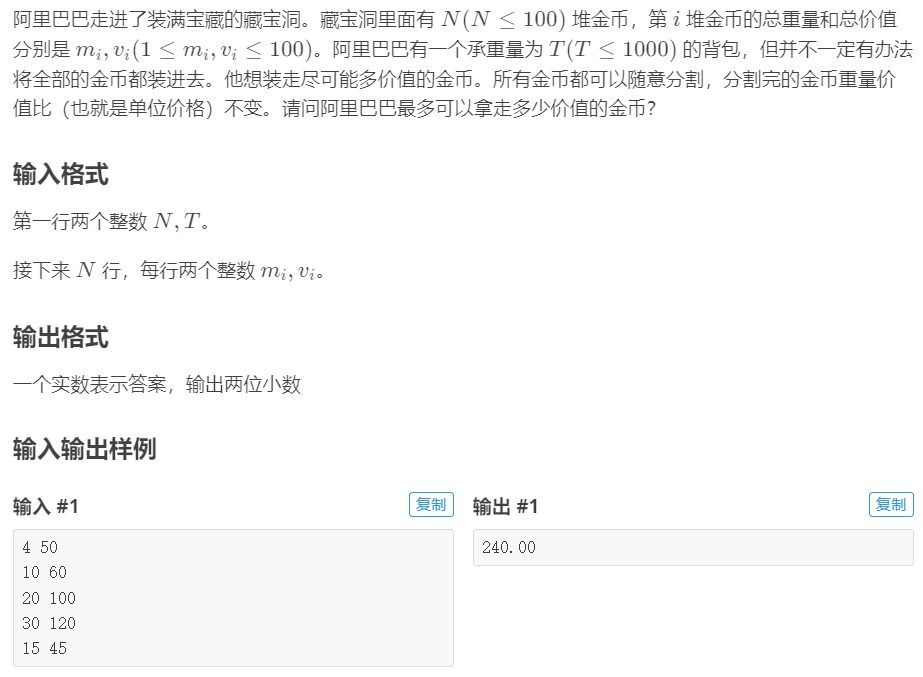
例题2 部分背包问题

分析

贪心选择性

可以按堆分成几个子问题，每个子问题按单价高的优先装入背包中，最后一堆装不下可以装部分

拆分的n堆金币，包括最后一堆的一部分，都比为未装入背包中的单价高，因此可以保证每次按单价高的局部最优保证全局最优

最优子结构

按堆分成一些子问题，这些子问题装入背包时，都是当前价值最高的，达到局部最优解，这些局部最优解组成了装入背包的全局最优解

因此，按照价值高的贪心策略，优先装入背包中，装最后一堆时，如果装不下，就装部分金币到背包

参考程序

#include<bits/stdc++.h>
using namespace std;
const int MAXN=105;
int n,t;
struct mvp{
	int m;//重量
	int v;//总价值
	float p;//单价
};
mvp mvps[MAXN];
bool cmp(mvp mvp1,mvp mvp2){//排序规则 按单价从大到小
	return mvp1.p>mvp2.p;
}
float ans;

int main(){
	cin>>n>>t;//n金币数 背包承重
	for(int i=0;i<n;i++){//每个宝藏的种类 总价和单价
		int m,v;
		cin>>m>>v;//输入重量 总价
		mvps[i].m=m;
		mvps[i].v=v;
		mvps[i].p=v*1.0/m;//计算单价
	}
	
	sort(mvps,mvps+n,cmp);//按单价从大到小排序
	
	for(int i=0;i<n;i++){
		if(t>=mvps[i].m){//重量t>这堆金币的重量 装入这堆
			t-=mvps[i].m;//装入 t 的承重减少
			ans+=mvps[i].v;//ans累计这堆总价值
		}else{//ans累加这堆的一部分价值
			ans+=mvps[i].v*1.0/mvps[i].m*t;
			break;
		}
	}
	cout<<fixed<<setprecision(2)<<ans;
}

CSP初赛复习-26-贪心算法-练习题
https://www.cnblogs.com/myeln/articles/17624142.html