深度学习中的优化算法

1. 基本算法

1.1 随机梯度下降

1.2 动量算法

1.3 nesterov动量算法

2. 自适应学习率算法

2.1 AdaGrad

2.2 RMSProp

2.3 Adam

 

1.1 随机梯度下降

        从数据集中随机抽取m个小批量样本（满足样本独立同分布），这样对每一个样本计算前馈损失，然后用前馈损失对网络的参数求导，获得梯度值。之后对这m个样本的梯度求均值，该梯度均值为估计总体网络参数应该向什么方向行走的无偏估计。

算法描述：

参数：学习率ε、初始参数θ

while 未满足终止条件:

    从训练集中随机抽取m个样本$\left\{ x^{(1)}, x^{(2)}, …，x^{(m)} \right\} $,每个样本$x{(i)}$对应一个标签$y{(i)}$；

    计算m个样本的平均梯度：$\hat{g} \leftarrow +\frac{1}{m} \nabla_{\theta_t} \Sigma_{i} L\left(f\left(x^{(i)}, \theta_t\right), y^{(i)}\right)$

    更新参数: $\theta_{t+1} \leftarrow \theta_t – \epsilon \hat{g}$

end while

 

1.2 动量算法

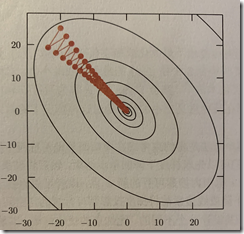
动量算法提出的目标在于加速算法学习。特别针对高曲率、小但一致的速度，或速度带有噪声的情况。（解决hessian矩阵病态条件和随机梯度的方差）

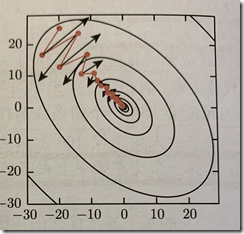
左：具有病态条件下的普通梯度下降 右：病态条件细下的动量算法

参数：学习率$\epsilon$，衰减率α，初始参数$\theta$，初始速度v

while 未达到终止条件：   

    从训练集中随机抽取m个样本$\left\{ x^{(1)}, x^{(2)}, …，x^{(m)} \right\} $,每个样本$x^{(i)}$对应一个标签$y^{(i)}$；

    计算m个样本的平均梯度：$\hat{g} \leftarrow +\frac{1}{m} \nabla_{\theta_t} \Sigma_{i} L\left(f\left(x^{(i)}, \theta_t\right), y^{(i)}\right)$

    速度更新：$v_{t+1}  \leftarrow \alpha v_t – \epsilon g$

    参数更新：$\theta \leftarrow \alpha + v$

end while

从描述可知，动量算法每次迭代用速度v去更新参数，并且每个迭代周期都会有固定的α∈（0,1）的衰减，这得优化过程的步幅会越来越小，能很快地找到极值。实践中，α通常取0.5/0.9/0.99。

 

1.3 nesterov动量法

nesterov动量法和动量法很像，区别在于nesterov动量法在计算梯度上，不是使用上一轮的更新参数$\theta$,而是$\theta + \alpha v$

它能改进凸批量梯度情况下的误额外差收敛率，但是对随机梯度情况下没有影响。

 

2. 自适应学习率算法

学习率是迭代过程中参数从梯度中获得多少程度更新值的一个超参数，而且学习率是难以设置的超参数之一，并且对模型的优化有着显著的影响。自适应学习率算法是使每次参数更新的过程中，每个参数学习率都不相同。

 

2.1 AdaGrad

自适应梯度算法的核心是使具有大偏导数的参数学习率更大，具有小偏导数的参数它的学习率更小。它使用求得的对参数的梯度向量，用element-wise的操作获得设置不同参数学习率的依据。

这种优化方法在部分深度学习模型上有不错的效果。

参数：全局学习率$\epsilon$，初始参数$\theta$，小常数$\delta$(目的是为了数值稳定，参考值$10^{-7}$)

初始化梯度累积变量$\gamma$=0

while 未达到终止条件：

    从训练集中随机抽取m个样本$\left\{ x^{(1)}, x^{(2)}, …，x^{(m)} \right\} $,每个样本$x^{(i)}$对应一个标签$y^{(i)}$；

    计算m个样本的平均梯度：$\hat{g} \leftarrow +\frac{1}{m} \nabla_{\theta_t} \Sigma_{i} L\left(f\left(x^{(i)}, \theta_t\right), y^{(i)}\right)$

    累积平方梯度：$\gamma \leftarrow + g \odot g$

    参数改变量计算：$\Delta\theta \leftarrow -\frac{\epsilon}{\delta + \sqrt{\gamma} }\odot g$（这里跟$\gamma$相关的操作都是element-wise处理）

    参数更新：$\theta_{t+1} \leftarrow \theta_t + \Delta\theta $

   

 

 

2.2 RMSProp

RMSProp是目前深度学习从业者经常采用的优化方法之一。已被证明有效且实用

RMSProp相比AdaGrad算法在非凸设定下的效果更好。

RMSProp使用指数衰减平均来丢弃遥远过去的信息，使其能够在凸结构中快速收敛。

RMSProp有标准形式以及结合Nesterov动量形式。

参数：全局学习率$\epsilon$，初始参数$\theta$，小常数$\delta$(目的是为了数值稳定，参考值$10^{-6}$)

初始化梯度累积变量$\gamma$=0

while 未达到终止条件：

    从训练集中随机抽取m个样本$\left\{ x^{(1)}, x^{(2)}, …，x^{(m)} \right\} $,每个样本$x^{(i)}$对应一个标签$y^{(i)}$；

    计算m个样本的平均梯度：$\hat{g} \leftarrow +\frac{1}{m} \nabla_{\theta_t} \Sigma_{i} L\left(f\left(x^{(i)}, \theta_t\right), y^{(i)}\right)$

    累积平方梯度：$\gamma \leftarrow  \rho \gamma +\left(1-\rho \right) g \odot g$

    参数改变量计算：$\Delta\theta \leftarrow -\frac{\epsilon}{\delta + \sqrt{\gamma} }\odot g$（这里跟$\gamma$相关的操作都是element-wise处理）

    参数更新：$\theta_{t+1} \leftarrow \theta_t + \Delta\theta $

参数：全局学习率$\epsilon$，累计梯度衰减率$\gamma$，动量衰减率α，初始速度v,初始参数$\theta$

初始化梯度累积变量$\gamma$=0

while 未达到终止条件：

    从训练集中随机抽取m个样本$\left\{ x^{(1)}, x^{(2)}, …，x^{(m)} \right\} $,每个样本$x^{(i)}$对应一个标签$y^{(i)}$；

    \tilde{\theta} \leftarrow \theta + \alpha v

    计算m个样本的平均梯度：$\hat{g} \leftarrow +\frac{1}{m} \nabla_{\tilde{\theta}} \Sigma_{i} L\left(f\left(x^{(i)}, \tilde{\theta} \right), y^{(i)}\right)$

    累积平方梯度：$\gamma \leftarrow  \rho \gamma +\left(1-\rho \right) g \odot g$

    参数改变量计算：$v \leftarrow \alpha v-\frac{\epsilon}{ \sqrt{\gamma} }\odot g$（这里跟$\gamma$相关的操作都是element-wise处理）

    参数更新：$\theta_{t+1} \leftarrow \theta_t + v$

 

2.3 Adam算法（自适应动量算法）

Adam算法对超参数的选择相当鲁棒

步长：$\epsilon$ (建议0.001)，矩估计的指数衰减速率$\rho 1$∈[0,1) $\rho 2$∈[0,1) (建议默认分别为0.9,0.999)，小常数$\delta$(目的是为了数值稳定，参考值$10^{-8}$)，初始参数$\theta$

初始化一阶、二阶矩变量$s=0$, $\gamma$=0

初始化时间步$t=0$

while未到达终止条件：

    从训练集中随机抽取m个样本$\left\{ x^{(1)}, x^{(2)}, …，x^{(m)} \right\} $,每个样本$x^{(i)}$对应一个标签$y^{(i)}$；

    计算m个样本的平均梯度：$\hat{g} \leftarrow +\frac{1}{m} \nabla_{\tilde{\theta}} \Sigma_{i} L\left(f\left(x^{(i)}, \tilde{\theta} \right), y^{(i)}\right)$

    $t \leftarrow t+1$

    更新有偏的一阶矩估计：$s \leftarrow \rho1 s +\left(1- \rho 1 \right)g$

    更新有偏的二阶矩估计：$s \leftarrow \rho2 \gamma +\left(1- \rho 2 \right)g\odot g$

    修正一阶矩偏差：$\hat{s} \leftarrow \frac{s}{1- \rho_1^t}$

    修正二阶矩偏差：$\hat{\gamma} \leftarrow \frac{\gamma}{1- \rho_2^t}$

    参数改变量计算：$\Delta\theta = –\epsilon \frac{\hat{s}}{\sqrt{\hat{\gamma}}+ \delta}$

    参数更新：$\theta \leftarrow \theta +\Delta\theta$

end while