【最优化】几何概念概述
根据最优化导论的相关概念做一个基本的概述和理解；
线段：
以往直线都是针对于二维和三位情况下进行讨论，从来没进行过高维下的线段讨论；
对于直线来说，直接定义就是方向向量+一点即可；
但是对于线段来说采用方程的常规设法，来张成一个解区间，进行表示线段；
假设对于n维空间下两点，如果采用向量表示，有x,y两点；
设，z位于两点连接线段的任意一点，则有：
z-y=α(x-y)
其中α位于[0,1]区间内；
对于这个式子其实有点抽象，因为x,y是采用向量表示，从一维二维甚至多维依然有效，本质上就是各个坐标方向的点的计算，z向量也是各个坐标轴上的点数值；
所以化简就有z=αx+(1-α)y；
这就是线段的表示，也就是线段点的集合；
超平面和线性簇：
书上并没有对这两个概念进行解释，似是而非，这里说一下个人的理解；
超平面：
所谓超平面就是多维空间下能够将空间分为两个不重叠互补的子空间的平面。通常来说超平面是低于空间维数n的，但是不一定是子空间(因为超平面有时候不过原点)；
超平面的表示由空间下的一个法向量来确定，也就是距离原点距离b下的和法向量正交的所有向量所构成的一个平面；
通常表示为：u=[u1,u2,u3...un]T，uTx=v；
其中x就是该平面上的所有点，v是距离原点的距离；
当v=0的时候，该超平面过原点，且为多维空间Rn下的一个子空间；
因此，超平面也把多维空间分割为两个子空间：
uTx>=v，正半空间；
uTx<=v，负半空间；
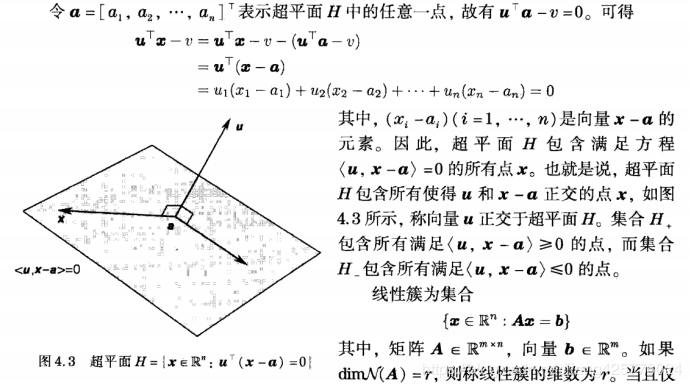
线性簇：
所谓线性簇就是多个超平面的集合，对于m个n维空间下的线性簇，可以简洁的表示为：
Ax=b，x，b都是向量，代表各个超平面下的u，原点距离b；
凸集：
所谓凸集，官方定义为：
对于一维或者高维情况下，对于已知的两点u,v，且两点在Rn可以表示为集合{w属于Rn：=αu+(1-α)v,α∈[0,1]},则称w点u，v的凸组合；
其实简而言之说人话就是指：如果一个集合W，内部的任意两点所连的线段上的点都在该集合内，就可以认定为这是一个凸组合；
因此：空集、单点集合、一条直线或者线段、子空间、超平面、线性簇、半空间、全集都是凸集；
例如书上给出的经典凸集合：
对于凸集，有如下推广性质：
若有凸集A，B；
则A+B={x=u+v}，仍然属于凸集；
则A∩B，仍然属于凸集；
则βA，仍然属于凸集；
书P34给了三种情况的详细论证，使用定义来进行论证；
邻域：
在考研的高等数学中，简单的研究过领域的概念；
也就是对于一点x，存在y∈Rn，使得||y-x||<σ，所以领域可以视为一个以x为中心点，σ为半径的球体；
关键是区分 开集、闭集、紧集三个概念；
首先要说一下边界点得问题：
对于一个集合S。
如果存在x某个领域所有的点都属于S，则x称为S的内点；
如果存在x的领域内一部分点属于S，一部分点不属于S，则称x为S的边界点，边界点的集合也就是S的边界；
而开集、闭集、紧集这三个概念立足于边界定义之上：
开集：S包含其集合点的所有领域；实际理解就是不存在边界点，仅仅有内点。推广到一维情况，典型的就是(1,2)集合，而x=1,x=2都为该集合的边界点；
闭集：S包含边界点，如果一个集合补是开集，则该集合必定是闭集，典型的为[1,2]；
紧集：S有界且为闭集；
所以简而言之闭集、紧集可以取到边界曲线上的值，对于求解局部极值多了一条曲线取值点，这个是以往高等数学边界求极值的概念化的表示；
多面体和多胞体：
对于多维下的凸集，已经给过证明，多面体其实是凸集合的延伸概念；
对于某一个凸集合，在其边界点可以找到一个超平面，使得整个凸集都处于一个半平面内，该超平面称之为支撑超平面；
由于半平面也为凸集，凸集的交集也为凸集，所以多个使用多个支撑半平面相交，得到多个半平面交集，该集合为凸集，称之为多面体；
而多胞形就是非空有界的多面体；
