【理论基础】神经网络及相关基础概念

神经网络基本思想：

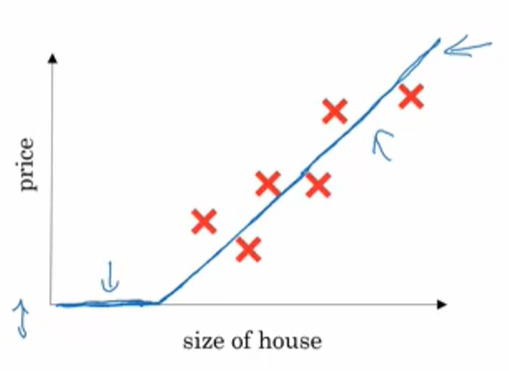
相当于逻辑回归问题，进行高维下的类曲线模拟，从而解决一个有监督的分类问题；

 

神经网络一些术语：

1.ReLU函数（rectified linear unit，即修正线性单元）：

 

基本函数图像如上所示，其中θ参数值为直线和横坐标的交点，要求x取值应该大于等于 θ；

 

2.有监督学习：

需要将数据打标签，多用于分类；

 

3.结构数据和非结构数据：

结构数据：类似于数据库SQL表类型，每个特征有清晰的定义；

非结构数据：原始的音频，图像，语句。例如图像像素、语义等结构的数据；

 

逻辑回归：

就是一个简单的二分类问题；

通常采用y=WTx+b来表示。

其中WT和b代表参数，x代表输入，y代表预测值；

但是对于二元分类问题，往往希望y处于[0,1]范围内，所以但是y有可能超过范围。

所以采用sigmoid函数，将y值映射再[0,1]之间；

 

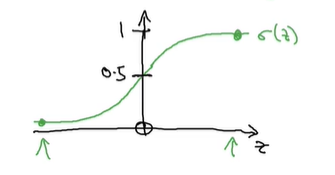
所以常表示为：y=σ（WTx+b）；

 

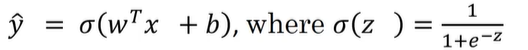
对于单个样本损失函数，有以下形式，可以在是的Loss minmize的同时，是的和实际值相近：

 

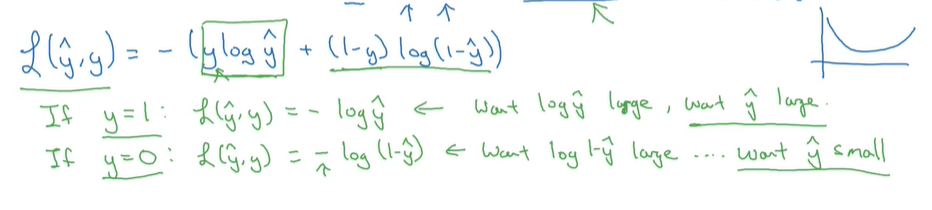
对于整体训练集的成本函数，用于衡量整个样本下的w和b参数的训练效果，有：

 

 

代表整个样本下的，所有损失函数最小化的集合版本；

对于J(w,b)，在空间下的表示为一个凸函数：

 

 

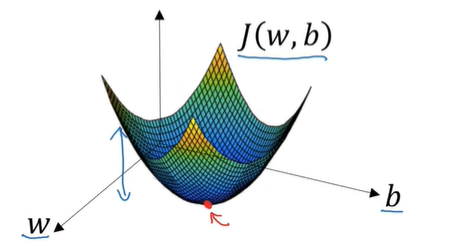
所以对于minmize J，相当于找空间的最低点，通常的方法采用梯度下降来进行最低点的寻找。

对于地图下降，更新形式为使用各个方向的偏导来进行梯度下降；

例如，对于参数w，有：

 

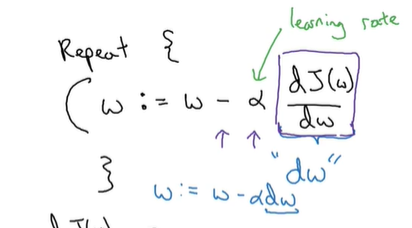
 其中，α代表学习速率，代表每次更新w的步幅长度；

对于二维凸函数来说，各个方向的也必定是凸函数；

所以对于曲线某点求导，当设置学习速率，无论在最低点的哪个方向，都可以使得由于导数方向正负的不同加减不同的值，来逼近最低点；

 

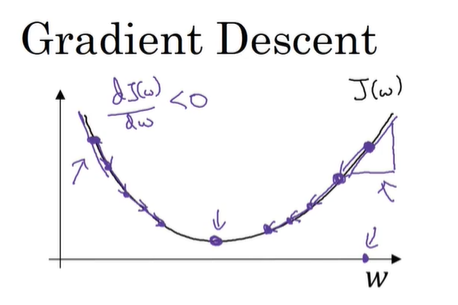
b值得更新同理，所以可以在二维图像上无限逼近于最低点；

反向传播：

反向传播依据的是计算图理论，也就是多元微分学得链式法则，通过链式偏导公式来计算相应的影响值，也就是通过某个变量的改变，会导致J变化得成都是多少；

例如J函数具有以下计算图：

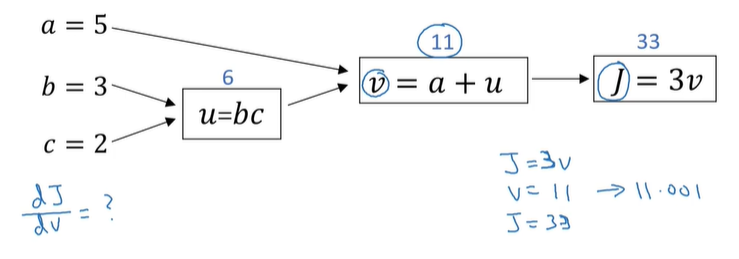
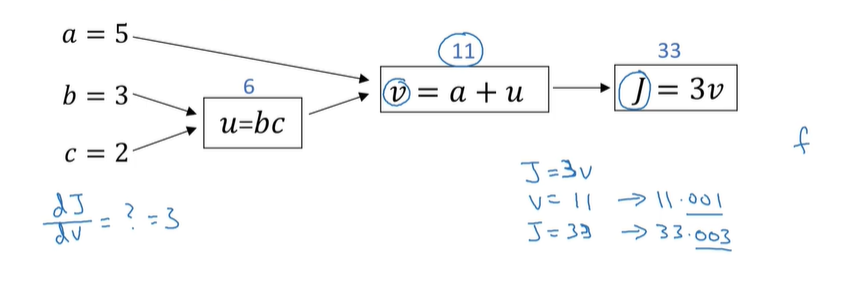
 例如：

 

 

简而言之，反向传播得意义就是进行下一步更新；

即得到相应的偏导数，进行下列公式的反复迭代计算，更新w和b，是的代价函数最小；

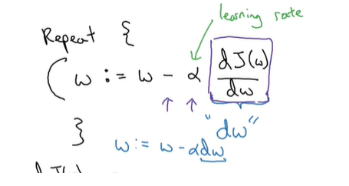
所以，将整个训练过程，如果推广到m个训练样本，整个数据集采用向量表示。

各个反向梯度得参数导数形式为：

所以对于整个流程为（如果采用朴素for循环表示）：

 

---

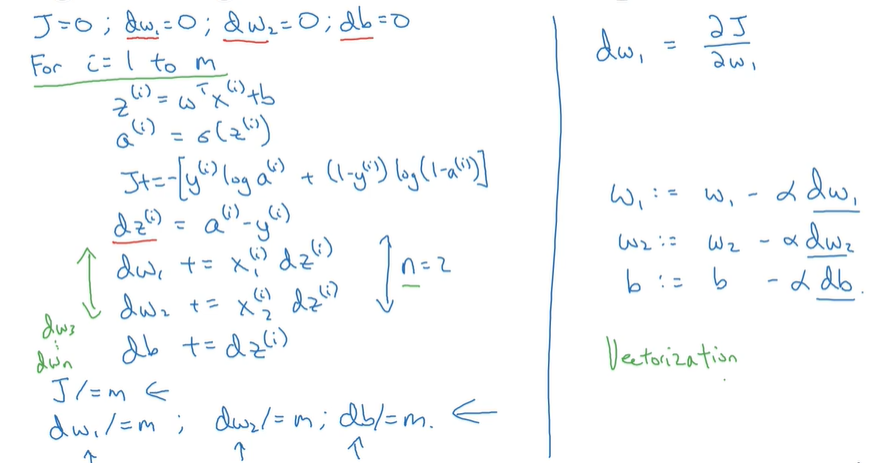
这里注意一下左边绿色箭头部分：

 

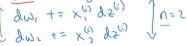
 这个是根据链式偏导求得的，也就是假设

 

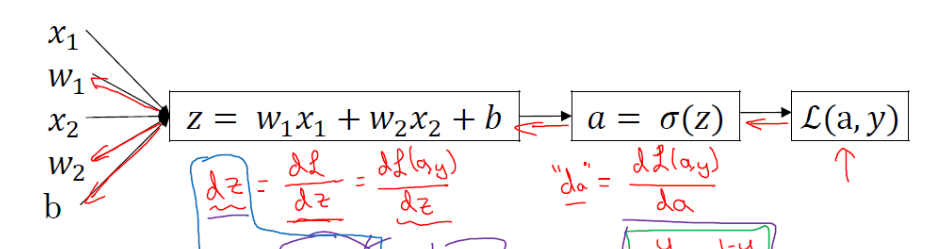
 通过链式求导化简即为该函数，中间省略了几步。

---

 

 

但是对于非向量计算，只采用for循环是效率低下的，如果采用向量化计算可以很好的避免这个问题；

对于普通的计算：

 

 两者的差距如下（使用向量可以很好的省去循环的问题，直接采用numpy中的向量相乘即可）：

 

神将网络下得节点表示：

 

 

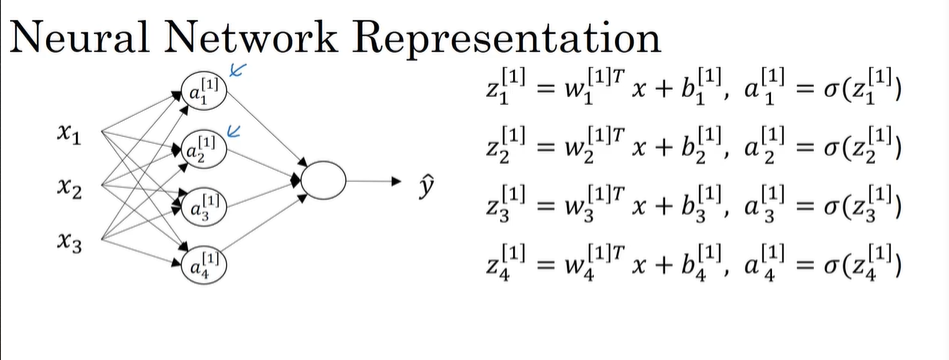
右边式子代表隐含层得输出值，如果采用想向量表示隐含层的输出变换，可以得到以下形式：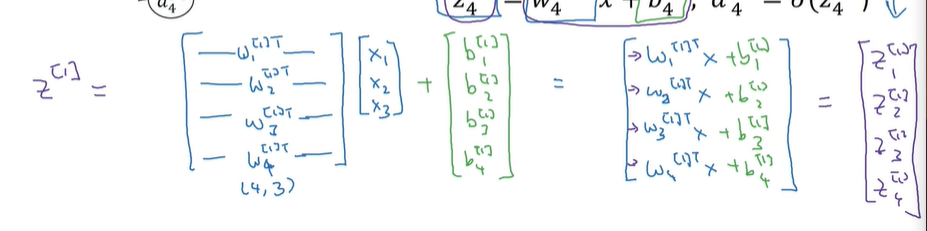

 

 

其中上图的x代表向量[x1,x2,x3]；

所以按照上述得输出网络得最后一层，可有：

 

 

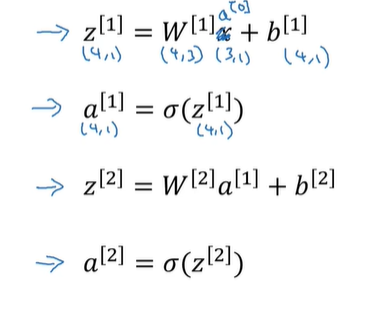
对于m个样本下的神经网络推导：

 

 

 

 

 

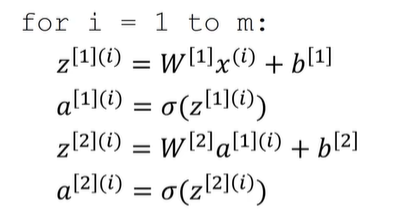
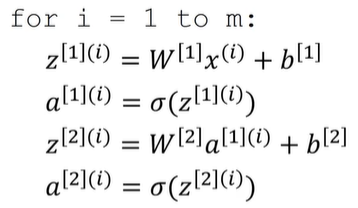
同样的，如果将m个样本，构成一个样本矩阵：

 

 

 

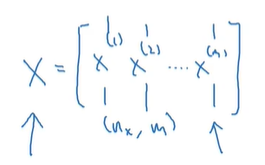
可以通过向量化来进行简便计算：

 

 

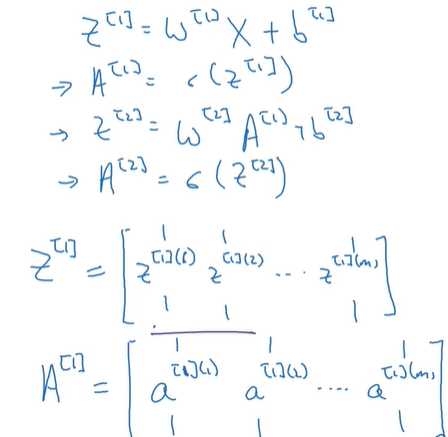
其中A[1]代表第一层的各个神经元节点的输出，也就作为下一层的输入；

因此，n层的迭代计算可以直接化简为n次矩阵乘积；

---

这里再补充一下关于W矩阵的问题：

W矩阵为一个层得多个节点参数构成，为m*n矩阵；

m代表该层节点个数，而n代表特征个数；

对于典型的一层情况，可以理解为下图：

 

 

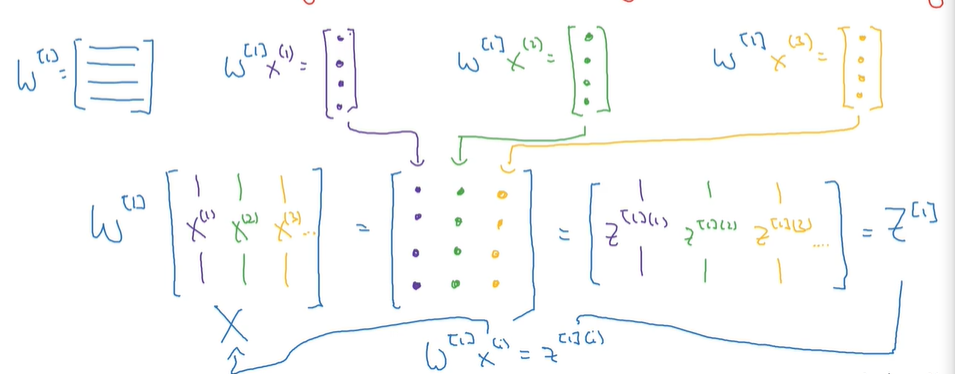
后续得z矩阵得各列代表各个样本通过该层计算所得到的下一层的输入值，整个矩阵类似于下一层的输入值，作为新的X样本进行输入；

 

激活函数：

类似于sigmoid，对于计算值进行平滑操作，例如tanh函数；

 

 

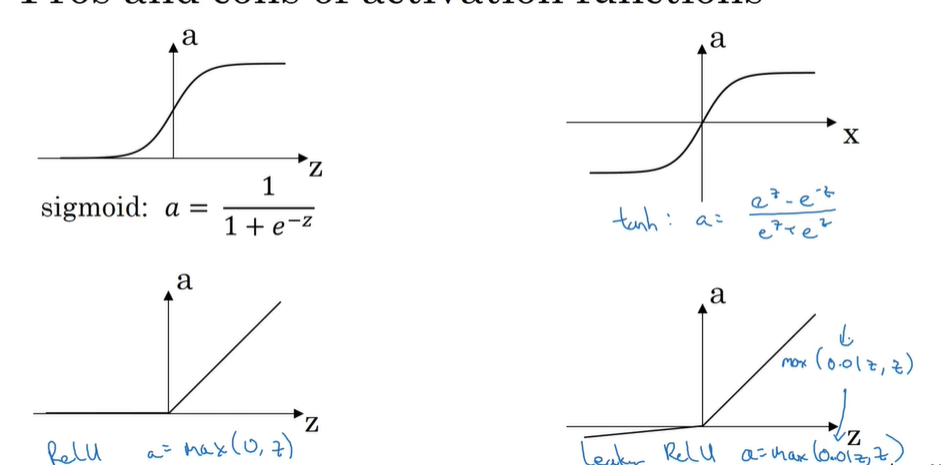
sigmod一般用于二元分类，tanh效果大于sigmoid，但是Relu更加常用；

 

线性激活函数：

类似于不适用sigmoid这种变换函数，直接恒等或恒等+偏量；

 

 

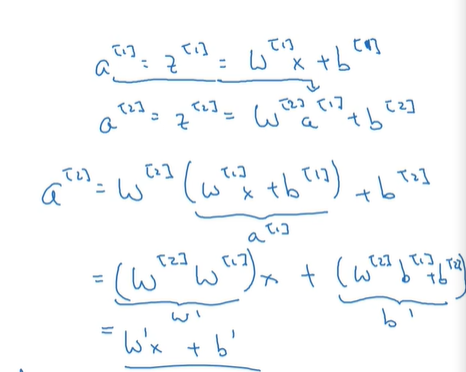
如果一直在神经网络中使用线性函数，隐藏层等于没用，相当于直接就是一个大的W直接在更新；

 

非线性激活函数：

通过非线性激活函数可以得到某种目的，满足对于最终与测量的需求，例如回归预测，二值分类等；

 

神经网络中的梯度下降方法：

和单个神经元类似，只不过神经网络由于是多个神经节点项链，并且W是参数矩阵，略有些不同；

例如，对于双层单节点结构（这里需要注意的是单个节点输入是单参数，所以只有一个w）：

 

 上图代表两个神经元，分别作为两层，同样的，如果根据反向推导，可以得到：

 

 

 

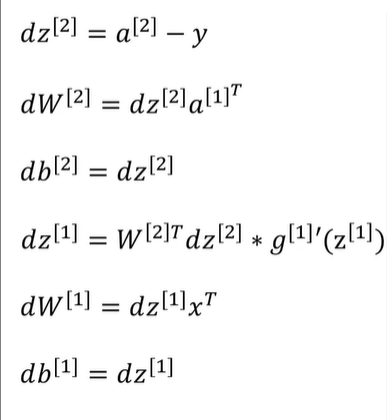
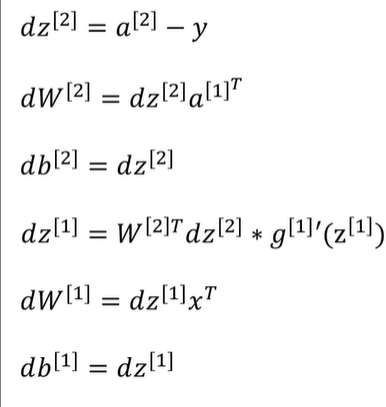
 如果单节点设计多参数，则w采用矩阵和向量表示，并且如果采用m个样本进行同一批训练：