Crypto基础
工具
ciphey
一个很牛的解密软件,用了AI来辅助。
记得下载的时候windows只支持python3.9以下(这里有点坑),我使用python37(不用虚拟环境啥的,ciphey会自动调用的,本机是python3.11)。
There are 3 ways to run Ciphey:
File Input: ciphey -f encrypted.txt
Unqualified input: ciphey -- "Encrypted input"
Normal way: ciphey -t "Encrypted input"
windows在环境变量中添加PYTHONUTF8=1就能避免ciphey报错gbk问题。
Sagemath
求多项式
使用CopperSmith方法,可以求e阶多项式f模n的两种根:
- \(root < n^{\frac{1}{e}}\)
- 给定β,要得到模p(p是n的因数)下的小根,并且:\(p≥n^\beta\)
PR.<x> = PolynomialRing(GF(p))
f = a*x^3 + b*x^2 + c*x + d - y
f = f.monic()
res = f.small_roots()
m = int(res[0])
print(long_to_bytes(m))
数学知识
离散基础知识
Y 是 rand,X 是 independent uniform var(独立均匀变量),那么$ Z=Y \oplus X $肯定是 Uniform var。
这反应了异或最重要的特性,能掩盖原码(即使是概率也能被掩盖),这也是One-Time-Pad成立的基础。
数论基础知识
同余
- 对称性:$ a \equiv b ↔ b \equiv a\pmod{p} $
- 传递性:$ (a\equiv b) and (b\equiv c)→a \equiv c \pmod p $
- 结合律:$ ((a+b)modp+c)modp=(a+(b+c)modp)modp $
- 分配率:$ (((a+b) \mod p) \cdot c) \mod p = (ac \mod p + bc \mod p) \mod p $
重要的是每次运算都要在当前群上面取值(也就是取模)即可。
符号
- $ Z_n $表示一个正数(在模 n 之下)。比如:5x7=11 in $ Z_{12} $。
- $ x^{-1} $ 逆元(Modular Inversion)指的是在 $ Z_N $ 内 $ xx^{-1}\equiv 1(mod~N) $,其中x和N必须互质。
- 我们这里的关键点是$ x^{-1} $,也就是可以把它看作这个方程的解 \(x^{-1}x-1=bN\)(N 的 b 倍)。根据贝祖定理,这等同于求\(x^{-1}x+bN=1\),也就是x和N必须互质。
仅有 gcd(x,N)=1 的时候才有逆元
- $ Z_N^* $ 定义为能模逆的集合(也就是和 N 互质的集合,不包括 0)。比如:$ Z_{12}^* $ ={1,5,7,11}。
很明显N为质数的时候就和 \(Z_n\) 几乎相等,只不过这个不包含0。
- ax+b=0(模一次线性方程),也就是求 $ x=-b·a^{-1} $in $ Z_n $,用 Euclid 寻找 a。
贝祖定理
gcd(greatest common divisor)表示 x,y 的最大约数。比如:gcd(12,18)=6。如果 gcd=1,那么 xy 就是互质(relatively prime) 的。
贝祖定理即:
比如:2x12-1x18=6,这里的(a,b)=(2,-1)
快速找到(a,b)的方法是 Extended Euclid alg.(扩展欧几里得算法,时间复杂度为$ O(log^2N) $)
费马小定理(Fermat's theorem)
假设存在一个集合 $ A: { 1,2,...,p-1 } $,由于里面的所有元素肯定和质数p互质,那么我们可以肯定A里面的任何一个元素乘上a以后还是和p互质的: $ gcd(A,p)=gcd(A*a,p) $
我们还能肯定的说,Axa只是改变了顺序,每个Axa % p以后都会再次落入集合A中不会碰撞,为什么呢?因为如果发生碰撞意味着:Ai xa= Aj xa(mod p),如果两边同时除以a就会发生Ai = Aj,但是这在一开始就是矛盾的。所以我们会知道Axa的步骤其实只是打乱了集合A的顺序,并没有产生碰撞。
那么此时很明显就有: $ (p-1)! a^{p-1} \equiv (p-1)! \pmod p $,得证。
- 模逆的另一种计算方法(只适用 N 为素数的时候):\(x^{-1}=x^{p-2}\) ,时间复杂度 O( \(log^3p\) )。
- 时间复杂度计算:p 表示为二进制数是 \(log_2p+1\) 位( \(2^{n-1}<p<2^{n}\) )
- 那么根据快速模幂计算过程,就要进行 $ O(log_2(p-2))≈O(log_2p) $ 次乘法
- 根据大数乘法,每次乘法的单次模运算需要 $ O(log_2p)^2 $
- 产生随机素数:现在已经有更好的方法,并且这种方法产生的素数有可能是合数(只是概率非常非常小),相当于这里的费马定理就是作为一个验证方式:
- 在所选定的区间随机取一个 p\(\in [2^n,2^{n+1}-1]\)
- 验证\(2^{p-1}是否在Z_p\)中,如果不是就重复第一步
快速模幂运算
快速模幂运算实际上就是不断用小的模幂去凑大的模幂,比如 \(7^{4}\pmod{13}=7^2\pmod{13}*7^{2}\pmod{13}=10*10\pmod {13}\)
只不过我们为了推广使用,用的是二进制幂数,所以每次都相当于减半:\(5^{117}=5^{1110101_2}\),这里碰到1才做一次乘方计算,一共要做\(log_2^p\)次,而乘法的复杂度是\({log_2^p}^2\)。
def fast_pow(base, exponent):
使用快速幂算法计算 base 的 exponent 次方。
result = 1 # 初始化结果为 1
while exponent > 0: # 当指数大于 0 时循环
if exponent % 2 == 1: # 如果当前指数是奇数
result *= base # 将当前的 base 乘到结果中
base *= base # base 自乘,相当于 base^2, base^4, base^8, ...
exponent //= 2 # 指数右移一位,相当于除以 2
return result
欧拉定理
费马定理的一般化:\(N=p·q,\phi(N)=\phi(p)\phi(q)=N-p-q+1=(p-1)(q-1)\):
- <g>的生成元:( generator of \(Z^*_p\))存在 \(g\in Z^*_p\)构成\(\{ 1,g,g^2,g^3,...,g^{p-2} \}\)=<g>,我们认为$Z^*_p $是一个 循环群(cyclic group)。比如:{1,3,3²...,\(3^5\)}={1,3,2,6,4,5}=\(Z^*_7\),那么 3 就是 generator。
- 为什么直到\(g^{p-2}\)?因为根据费马定理,\(g^{p-1}\)就是 1 了,相当于循环回去了。
- <g>的阶数:也就是<g>的大小。比如上面的\(ord_7(3)=6,ord_7(2)=3\)
- 拉格朗日定理:子群的阶一定是群的阶的因数,即:\(ord_p(g)\)divides (p-1)。
有趣的拉格朗日定理:我们根据子群h来构造陪集(加法群就是a+h,乘法群就是a·h),我们会发现陪集的数量x子群的阶数=群的阶数。
比如乘法群\(Z_7={1,2,3,4,5,6}\)生成元是3,我们取生成元2可以构造:{1,2,4},如果3xh就会构造出{3,5,6},刚好覆盖整个群。
其实用加法群更好理解,相当于在“平移”整个子群,直到覆盖完成。
所以子群的阶数(即里面元素的个数)最终肯定能通过a次“平移”覆盖整个群,也就是肯定是群的阶数的因数。
为什么能刚好覆盖完?不会出现子群阶是5覆盖不了群阶是13的情况?因为每个元素必须属于且仅仅属于一个陪集,也就是不能有重复的情况,如果阶是5的话3·h时第14/15就覆盖了陪集1·h的1/2
为什么“每个元素必须属于且仅仅属于一个陪集”?
- 覆盖性:任意g∈G,肯定存在aH使得g∈aH。这个好证明,取a=g即可,即所有元素至少属于一个陪集(自身生成的陪集)。
- 唯一性:若g∈aH且g∈bH,则aH=bH。取h1/h2∈H,如果\(ah_1=bh_2\),那么\(a=b(h_1^{-1}h_2)=bh'\),因为H是子群,h'/h∈H,所以hh'∈H(子群必须满足封闭性),所以aH∈bH。反之亦然,所以aH=bH。也就是说如果aH和bH重叠了,假设重叠的这个元素叫做h,那么从肯定是\(ah_1\)平移后落到h上,\(bh_2\)同理。但因为\(hh_1h_2\)都是H中的元素,有点像是线性代数的行列式变换一样,在b的角度看a,实际上移动的是一个\(h'\)元素落到h上,但是h'是属于bH的,所以我们能得出aH∈bH。因为子群和陪集都是一块一块的移动的,所以如果有一个点重合,说明所有点重合,不存在只有其中少数点重合。
群和子群
乘法群必须满足:封闭性和存在逆元。
让我们考虑生成元为3的群:
{3^0 3^1 3^2 3^3 3^4 3^5 3^6} % 7
{1 3 2 4 6 4 5 1}阶为6
不难看出,之所以费马小定理生效,因为里面每个元素 ^6过后都会变成 3^6 3^12 3^18...最后都是1。
子群是群的一部分,并且要满足乘法群的构造,那根据拉格朗日定理,子群的阶必须是群的阶的因数,不过这里要注意,并不代表子群的生成元一定是群的生成元!
比如子群{1,2,4}的生成元是2(此处可链接DSA理论)。
欧拉函数
欧拉函数指的是与N互素的数的集合。
如果是单因子(N=pq...r)的情况,\(\phi_N=(p-1)(q-1)...(r-1)\)
如果是多因子(\(N=p^{k_1}q^{k_2}\))的话,\(\phi_N=p^{k_1-1}(p-1)·q^{k_2-1}(q-1)\)
推理过程:
- 从单因子我们可以看出,每个因子带来的互素系数的个数,就是和N不互素的数的系数组合。
- \(N=p^{k_1}q^{k_2}\)的话,其中能被p整除的就是:\(1 \cdot n/p^{k_1}, 2 \cdot n/p^{k_1}, \cdots, p^{k_1-1}(p-1) \cdot n/p^{k_1}\),其中n/p是为了得到“p的倍数,和N不互素的数”。
- 自然的,p因子带来的互素个数(和N不互素)的系数就是\(p^{k_1-1}(p-1)\)。
扩展欧拉定理(欧拉降幂)
欧拉降幂,也就是可以 通过\(\phi(m)来调整降低指数\)。
\(a^b \equiv
\begin{cases}
a^{b \mod \phi(m)}, & \text{if } \gcd(a, m) = 1, \\
a^b, & \text{if } \gcd(a, m) \neq 1 \text{ and } b < \phi(m), \\
a^{b \mod \phi(m) + \phi(m)}, & \text{if } \gcd(a, m) \neq 1 \text{ and } b \geq \phi(m).
\end{cases}
\pmod{m}\)
简单理解就是因为 mod m 会导致结果集中在\(\phi (m)\)个数内,很容易想到会有循环(就是小学都会的,10%3=7%3=1),我们设最小 r 出现循环,最小循环节是 s,就有:\(a^r \equiv a^{r+s}\),那其实很好理解\(a^r \equiv a^{r+\phi(m)}\),那我觉得\(a^r \equiv a^{r \pmod \phi +\phi}\)也能理解了~(别搞证明了)
也就是b如果互质就能直接模\(\phi (m)\),如果不互质就只能当b大于\(\phi (m)\)时候才能模,并且最后要加回去。
欧几里得算法(辗转相除)
求 GCD 的递归方法,也就是 gcd(a,b)=gcd(b,r),最大公约数也是余数的约数。
所以用递归来做的话,就是一直迭代到 gcd(x,0)=x 的时候,得到的就是最大公约数 a。
def gcd(a, b):
return a if b == 0 else gcd(b, a%b)
而扩展欧几里得,实际上就是一直记录着 x 和 y 在递归中的变化,最后一层一层往回带自然就可以了:
\(\begin{cases}
gcd(a,b)=ax+by \\
gcd(b,r)=bx+(a-b*(a//b))y=ay+b(x-(a//b)y)
\end{cases}\)
现在让我们来看 gcd 迭代到最后的时候(r=0的时候):\(gcd(a_n,0)=a_n*1+b_n*0=a_n\)
这意味着最后一步的 x=1,y=0,此时就能往回带了:
\(x_{上层}=y_{下层},y_{上层}=x_{下层}-(a//b)y_{下层}\)
int exgcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1,y=0;
return a;
}
int d=exgcd(b,a%b,x,y);
int k=x; //k是下层的x
x=y;
y=k-a/b*y;
return d;
}
def extgcd(a, b):
if b == 0:
return a, 1, 0
g, x, y = extgcd(b, a%b)
return g, y, x - (a//b)*y
要注意 通解和特解:
$ a(x_0 + k \cdot b) + b(y_0 - k \cdot a) = ax_0 + akb + by_0 - bka = ax_0 + by_0 + k(ab - ba) $
最小公倍数
\(gcd(a,b) * lcm(a,b)=a*b\)
将最大公倍数从两个数之中分别拿走,那么这两个数肯定是互质的了。如果互质的话,最小公倍数不就是现在这两数的乘积?
中国剩余定理
必须是模数互质的时候,计算 mod(p)和 mod(q),就能算出 mod(n)下的值。
其实想法很简单,如果 \(\begin{cases}
x \equiv a_1 \pmod{n_1},\\
x \equiv a_2 \pmod{n_2},\\
x \equiv a_3 \pmod{n_3}
\end{cases}\),我们想让它在 \(\pmod n\)下面生效的话,必然构造出的是长这个样子:\(a_1*(n_2n_3)^{-1}*(n_2n_3)+a_2*(n_1n_3)^{-1}*(n_1n_3)+a_3*(n_1n_2)^{-1}*(n_1n_2)\),其中逆元的作用是为了在属于它的模下会自动消掉后面一坨,而后面一坨的作用是在不属于它的模下会自动成n的倍数自动消除。
def crt(n_list, c_list):
n = 1
for i in n_list:
n *= i
N = []
for i in n_list:
N.append(n//i)
t = []
for i in range(len(n_list)):
t.append(invert(N[i], n_list[i]))
summary = 0
for i in range(len(n_list)):
summary = (summary + c_list[i]*t[i]*N[i]) % n
return summary
扩展中国剩余定理
可以直接通过sympy中的库来解决:
from sympy.ntheory.modular import crt
M = crt(n_list, c_list)[0]
理论知识
在扩展 CRT 中,m1 和 m2 就不是互质的了,意味着找不到逆元。
\(\begin{cases}
a \equiv r_1 \mod m_1,\\
a \equiv r_2 \mod m_2
\end{cases}→k_1m_1-k_2m_2=r_2-r_1\)
要想解这个方程,根据裴蜀定理,我们知道:\(k_1m_1-k_2m_2=GCD(m_1,m_2)\),也就意味着判断是否有解:\(GCD(m_1,m_2)|r_2-r_1\)
那现在让我们将上面的式子凑出能用扩展欧几里得算法:
注意到裴蜀定理中是+号,那么我们是用扩展欧几里得算法得出的解\(\lambda_1 \lambda_2\)就是:\(\begin{cases}k_1 = \frac{r_2-r_1}{gcd(m_1,m_2)}\lambda_1 \\ k_2 = - \frac{r_2-r_1}{gcd(m_1,m_2)}\lambda 2\end{cases}\)
那我们不就得到特解:\(x^*=r_1+k_1m_1 = r_1 + \frac{r_2-r_1}{gcd(m_1,m_2)}\lambda_1m_1\)
现在问题是如何构造通解?我们要先解决两个问题:
- 通解应该长成什么样?
- 凭什么说这就是唯一通解?
对于第一个问题,我们猜测,既然\(\begin{cases}x \equiv r_1 \pmod {m_1} \\ x \equiv r_2 \pmod {m_2}\end{cases}\),那通解就应该是\(x ^ * + k\cdot \Delta\),这似乎是板上钉钉的,如果\(\Delta\)将整个整数集分为无数个从0~\(\Delta\)的类(我们称为等价类),那很明显如果“1是特解”,那么\(1+k\Delta\)当然都是特解。
那为什么这个类里面只有一个通解?就不能\(1+k\Delta和2+k\Delta\)都是通解?这也是为什么我们让\(\Delta=lcm(m_1,m_2)\)的原因。
我们假设a,b都是通解,那么\(a-b=0 \pmod{lcm(m_1,m_2)}\),意思就是说:①a和b都比lcm要小②a-b还要整除lcm,所以a=b。
不过到这里,似乎\(\Delta\)等于什么都行,都能证明是唯一解:)
import gmpy2
from functools import reduce
def exgcd(a, b):
if b==0: return 1, 0
x, y = exgcd(b, a%b)
return y, x - a//b*y
def uni(P, Q):
r1, m1 = P
r2, m2 = Q
d = gmpy2.gcd(m1, m2)
assert (r2-r1) % d == 0
l1, l2 = exgcd(m1//d, m2//d)
return (r1 + (r2-r1)//d*l1*m1) % gmpy2.lcm(m1, m2), gmpy2.lcm(m1, m2)
def CRT(eq):
return reduce(uni, eq)
if __name__ == "__main__":
n = int(input())
eq = [list(map(int, input().strip().split()))[::-1] for x in range(n)]
print(CRT(eq)[0])
e次方根
\(x,c\in Z_p\),我们定义\(x^e=c~in~Z_p\)称为 e'th root of c。
例如 e=1/3,就是要寻找:\(x^3\equiv 7(mod~11)\)。
就像上面的例子一样,我们希望寻找\(c^{\frac{1}{e}}\in Z_p\)什么时候存在,相当于在问有没有\(x^e \equiv c(mod~p)\)。
- 当 e 和 p-1 互质的时候:那么当 gcd(e,p-1)=1 的时候,即 e 存在逆元 d=\(e^{-1}\)的时候,\(c^{\frac{1}{e}}=c^d~in~Z_p\) ,即\(c^d\)就是c的e次根。
- 当 e 和 p-1 不互质的时候(比如 e=2,p 是 odd):我们定义 Q.R.(quadratic residue)也就是在\(Z_p\)内拥有平方根。那么平方根的数量自然是“集合内数量的一半+0”(0 是 0 的平方):\(\#Q.R.=\frac{p-1}{2}+1\)。我们定义“勒让德符号”:\(x^{\frac{p-1}{2}}\),因为欧拉发现:
\((\forall x\in Z_p^*~is~a~Q.R.)~x^{\frac{p-1}{2}}\equiv 1(mod~p)\)
算术算法
计算机保存大数通过 32 位一块保存,因为在 64 位机上就能用 64 位表示结果(\(2^{32}\times 2^{32}=2^{64}\))。
时间复杂度
主定理:专门用于计算“递归”的时间复杂度,你要是展开能算也行(比如下面的大数乘法)
\(f(n) = O(n^{\log_b a - \epsilon})\) (\(\epsilon > 0\)), then \(T(n) = \Theta(n^{\log_b a})\)
\(f(n) = \Theta(n^{\log_b a})\), then \(T(n) = \Theta(n^{\log_b a} \log n)\)
\(f(n) = \Omega(n^{\log_b a + \epsilon})\) (and \(af(n/b) \leq cf(n)\)), then \(T(n) = \Theta(f(n))\)
讲解
大数乘法
使用Karatsuba算法,时间复杂度为\(n^{1.585}\)。相当于4次乘法变成3次乘法,并且每一层递归规模都减半。
步骤就是“分治策略”:
- 将大数分为两部分:\(x = a \cdot 2^{n/2} + b\), \(y = c \cdot 2^{n/2} + d\)。
- 计算 \(ac\), \(bd\) 和 \((a + b)(c + d)\)。
- 合并结果:\(xy = ac \cdot 2^n + [(a + b)(c + d) - ac - bd] \cdot 2^{n/2} + bd\)。
为什么时间复杂度快了呢?使用递归树展开的话:
层级 0(n=8):
T(8)
|
+----+----+
T(4) T(4) T(4) (3 个子问题,每个规模 n/2=4)
|
+----+----+
T(2) T(2) T(2) (共 3²=9 个子问题,规模 n/4=2)
|
+----+----+
T(1) T(1) T(1) (共 3³=27 个子问题,规模 n/8=1)
那很明显\(T(8)=O(8)+3⋅O(4)+9⋅O(2)+27⋅O(1)\),推广到一般情况就是:\(T(n) = O(n) + 3 \cdot O\left(\frac{n}{2}\right) + 9 \cdot O\left(\frac{n}{4}\right) + \cdots + 3^{\log_2 n} \cdot O(1)\),等比数列求和公式是:\(\sum_{k=0}^{\log_2 n} \left( \frac{3}{2} \right)^k = \frac{\left( \frac{3}{2} \right)^{\log_2 n+1} - 1}{\frac{3}{2} - 1} \approx O \left( \left( \frac{3}{2} \right)^{\log_2 n} \right)\)
对数恒等式:\(a^{\log_b c} = c^{\log_b a}\)
所以:\(\left( \frac{3}{2} \right)^{\log_2 n} = n^{\log_2 (3/2)} = n^{\log_2 3-1}\)
使用主定理的话:
此处\(T(n) = 3T\left(\frac{n}{2}\right) + O(n)\),即\(a = 3\), \(b = 2\), \(f(n) = O(n)\)。
所以\(\log_b a = \log_2 3 \approx 1.585\), \(f(n) = O(n)\),\(n = O(n^{1.585 - \epsilon})\) (with \(\epsilon = 0.5\)), so \(T(n) = \Theta(n^{\log_2 3}) \approx \Theta(n^{1.585})\)。
重复平方算法
综述
RSA和DSA
试想现在A想发信息给B,那么B必须面对如下两个问题:
- 别人不能偷看A的信息
- 凭啥B收到的信息就是来自A的
为了解决第一个问题,就使用非对称加密RSA来解决,其解密原理是欧拉定理,基于“模幂求逆”和“大整数分解”这两个难题
给定\(m^e \equiv c \pmod n\),这在日常生活的实数域上面非常容易得到\(c^{\frac{1}{e}}=m\),但是在取模运算中,我们根本不知道“m乘自己e次取了多少次模”即“丢失了多少信息”。如果我知道它取了k次模的话,那我就能\(c+kn=m^e\)得到\(m^e\)在实数域上面的数是多少,就能开方,这就是第一个难题“模幂求逆”。
如果想遵守有限域的规矩,我们只能用\(m^{ed}\equiv m \pmod n\)来得到m,即欧拉定理。但是\(d=inverse(e,(p-1)(q-1))\),这就涉及第二个难题“大整数分解”,在已知算力下,我们几乎不可能只根据n暴力破解出它的因数p和q。
第二个问题则使用DSA来解决,基于“离散对数”难题,我们很难伪造签名的原因是因为不能把rs从指数上面取下来从而篡改。
很明显A得给自己的消息“签名”来证明是他发的,但是数字签名应该包括什么呢?
- A自己独有的秘密x
- 为了保证不同消息不同签名(消息签名唯一性),使用哈希值H(m)
- A添加进的随机数字k
那又有很明显的问题,如果签名\(s=f(x,H(m),k)\)的话,里面的xk都是B不知道的,怎么解密?这就用到“模幂求逆”这个难题了,我们只要给的是\(\begin{cases}
y=g^x \pmod p \\
r= g^k \pmod p
\end{cases}\)不就能放心的给出yr,而xk又是自己独有的?
那现在\(s=x+H(m)+k \pmod{p-1}\)的话,\(g^s \equiv g^{x+H+k} \equiv y \cdot r \cdot g^H \pmod p\)。我们称(r,s)是签名,y是公钥。
现在似乎很美好,只要发(s,y,r,p)让B自己验算就行了,也就是A告诉B:“没有我的xk的话,可没人能算出s是多少哦更不可能保证加入H(m)后的验算等式还能成立了”。可是B说:“真的吗,你的r和s都站在’地上的’,如果有人给我假的s,然后自己算出假的r给我不也行吗”,即\(r'=\frac{g^{s'}}{y*g^H}\)。
那几乎是相同的思路,我们不要让rs直接“站在地上”不就行啦,也把它举到指数的位置,一开始我们让:\(\begin{cases}
r=g^k \pmod p \\
s=\frac{H+xr}{k} \pmod{p-1}
\end{cases}\),那么验签方案就是\(r=g^k=g^{\frac{H+xr}{s}}= g^{\frac{H}{s}} \cdot g^{\frac{xr}{s}}=g^{\frac{H}{s}} \cdot y^{\frac{r}{s}} \pmod p\),这下好了,rs全都跑到指数上面去了,取都取不下来。这就是DSA主要基于的难题“离散对数DLP”,我们不能把指数取下来。
因为p取1024比特(比如rsa的n也是),rsp规模差不多,结果一个签名(r,s)就是2048比特。B说:“你最好缩减一点,一个签名就要256字节也太大了”。
A想到:根据费马小定理我们知道\(g^{p-1} = 1 \pmod p\),我们取一个子群不就行啦!子群在模p意义下也能成立,那我们就取\(g=h^{\frac{p-1}{q}}\),也就是\(g^q=1 \pmod p\),此时阶就被缩减到q了。
那最后的解决方案就是:
- 先找到阶为q的生成元g:\(g=h^{\frac{p-1}{q}} \pmod p\)
- 然后\(\begin{cases} r=g^k \pmod p \pmod q \\ s=\frac{H+xr}{k} \pmod{q} \end{cases}\)
- 验签方案就是:\(r=g^{\frac{H}{s}} \cdot y^{\frac{r}{s}} \pmod p \pmod q\)
格密码
格密码实际上并不是具体的哪一种密码,而是指的是那些利用格的密码的一类密码。所以格更像是一个数学工具,在Coppersmith方法中我们也能看到格的应用。
格说白了就是坐标系,也就是向量空间,但是把标量乘法中乘数从实数变成了整数,可以理解为就像离散对数一样,很多东西在离散点上都和在实数上一点都不相同。
示例
NTRU
经常被用来作为示例的是一个简单版本的NTRU密码:\(\begin{cases}
公钥:h = f^{-1}g \pmod p \\
私钥:f,g \\
加密:c\equiv rh+m\equiv rf^{-1}g+m \pmod p \\
解密:fc \equiv rg+fm \equiv fm \pmod g
\end{cases}\),由于\(f^{-1}\)是定义在p上的逆元,所以不能直接将\(rf^{-1}g+m\)去模g,只能去掉\(f^{-1}\)过后再模g。
这里的重点很明显是rg+fm,如果我想破解它的话,就要幻想自己拥有FG,使\(Fh \equiv G \pmod q\)成立,这样子就能变成\(Fc \equiv rG+Fm\),FG都是我给的,自然就能破解出来。
那么现在问题变成:\(Fh-kq=G\),但是我现在要把它写成这种形式:\(F(1,h)-k(0,q)=(F,G)\),有问题吗?没有问题(*^▽^*)
现在我说这个式子就像是裴蜀定理一样,我要找(F,k)系数使向量(1,h)和(0,q)的组合最短,找到了就能得到(F,G)。找到合适的Fk使得组合出的向量足够短,那FG就是合法的。凭什么?因为你解密的时候rg+fm<p才能正常工作,不然就丢失信息了。
让我们看看hq几乎和p都是一个量级的,要想几个很大的东西凑出一个小东西,方法很有可能就是唯一的,所以我说你找最短的应该可以!
背包密码
背包密码有很多,这里讨论超级递增序列(后一个数比前一个数大至少一倍)背包。
我们将消息m作为二进制看待\(m=1001011\),然后用m的每一位去决定是否挑选一个超级递增序列的元素(比如)\(r=\{2,2^2,2^3...2^n\}\),然后全部加起来作为密文S。很明显,解密就是贪心算法,从大往小遍历即可。
但是这没有任何加密的方法,我们引入互质的AB,将超级递增子序列进行混淆:\(M_i \equiv Ar_i \pmod B\),然后加密就是\(S=\sum x_iM_i\),因为我们并不知道这个原来的“超级递增序列r”长成什么样,我们就无法解密。
但是知道A的人当然可以解密,密文实际上就是\(C=Ar_1x_1+Ar_2x_2+...+Ar_nx_n \pmod B\),他自己算出\(A^{-1}\)就能轻松解密了。当然这里的要求还是乘上逆元消掉A后的密文不超过B,不然丢失信息了捡不回的。
现在让我们思考怎样解密,我们发现手头只有一个公式:\(S=\sum x_iM_i\),然后连NTRU的类似式子都没有,因为解密完全是基于自己已经得知子序列r是什么的前提下解密的。你说,我无计可施了,想要运用手头的公式居然只能幻想自己拥有\(x_1,x_2,x_3...x_n\),这样才能使用\(S=\sum x_iM_i\):
等等,不对!这个解那么短(x不是1就是0),居然是由那么大的基底(M肯定比1大很多吧)构成的,我敢说这个解有且只有一个!
构造格
通过上述的两个例子,我们可以意识到,首先我们可以“幻想”自己拥有解密所需的必要元素,然后列出对应的式子,基本构造是:
并且我们还能知道,为了让“解有且只有一个”,我们必须使其体量“极其悬殊”才行,在大部分题中,为了能让LLL算法有指定的帮我们找解,我们甚至还要人为地加上很大很大量在格里,才能使解相对于格来说很小很小,然后被求出来。
格的相关知识点
基本域
也就是格的基底围成的空间:
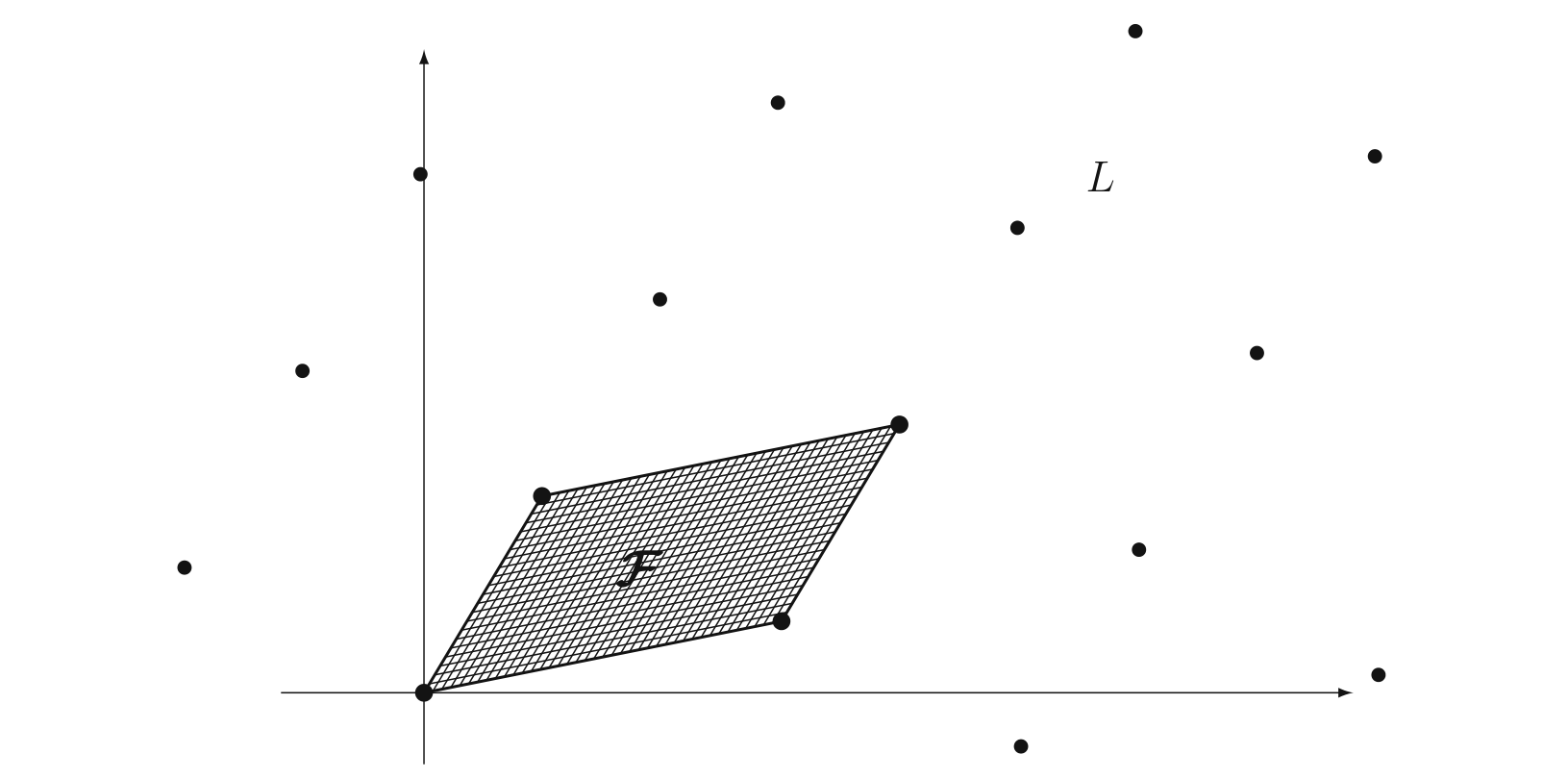
协体积
det在格里是协体积的意思,也就是一个格的基底可以很多(基本你任意取谁作基底都行),但是它的协体积都是一样的:
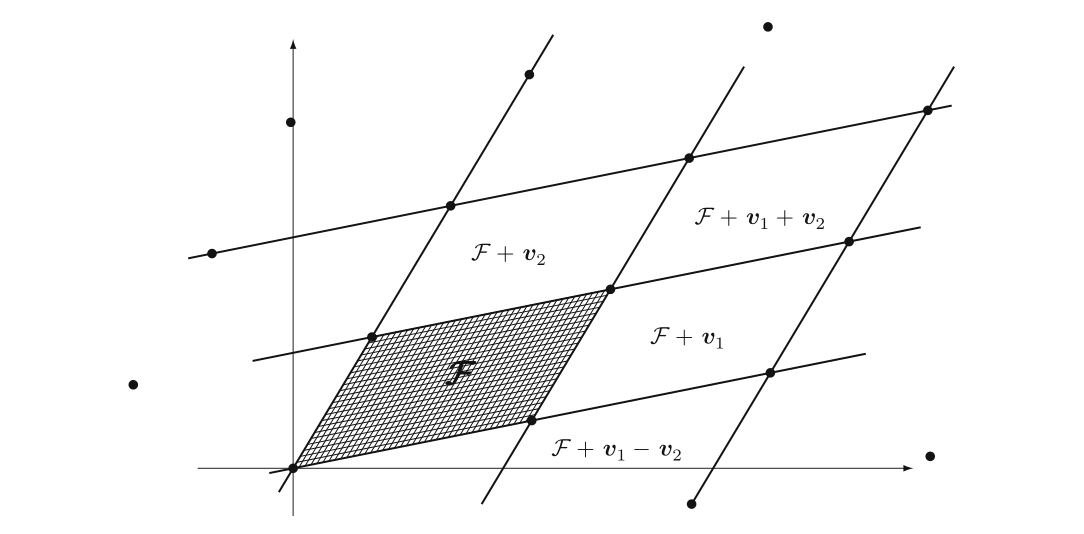
比如你取这个F反方向的两条作为基底也可以。
Hadamard 不等式
如果要协体积取最大,很明显只有正交的时候才会出现最大值:
SVP和CVP
SVP是最短向量问题,CVP是最近向量问题,SVP简单一点。
建议看这个视频讲明白SVP和CVP
Hermite定理
能被单独开标题的定理肯定有其重要之处,在前面我们总是凭感觉“感觉它足够短!”来求解,那么有没有具体的公式来告诉我们究竟在这个格里面,多短的向量才是值得我们关注的“最短向量”呢?
n是其格的维度,可以认为就是基向量的个数。我们这里有一些前人的经验,表明维度是如下的时候应该取多少(更精确一点,使用的时候记得开方再代入):
对于多个向量的话:\(\|v_1\| \|v_2\| \cdots \|v_n\| \leq n^{n/2} (\det L)\)(这个还没有使用过,用处不大)
证明
下面我们来证明,首先我们想象一个向量可以在格中作为球心构成一个球体,我们称为“闭球”。
现在我们有Minkowski's Theorem,如果闭球S是有界,对称(-a也存在S中),凸(S中的两个点连线也在S中),闭的(边界上的点也在S中):$$\text{Vol}(S) \geq 2 ^n \det L,则S肯定包含非零向量$$
明可夫斯基证明很简单,如果把S变成\(\frac{1}{2}S\),协体积肯定变成\(Vol(\frac{1}{2}S)=\frac{1}{2^n}Vol(S)\)。
那既然缩小1/2过后还是大于det(L)的(现在你知道为什么公式中要大于\(2^ndet(L)\)吧),那么假设原本S上有两点ab坍缩过后到同一点,这两点的连线中点根据“凸”的那么肯定也在\(\frac{1}{2}S\)里,证明完毕。
现在让我们回过头看Hermite定理的证明,我们这次不取球了,我们构造一个超立方体,棱长为2B(正负半轴每一边是B),同样的,它的\(Vol(S)=(2B)^n\)。
根据明可夫斯基定理,这个棱长最小能取到\(B=det(L)^{\frac{1}{n}}\),接下来求范数就可以啦:
证明完毕。
正交基和LLL
我们构造的格大多都不够好,越接近正交基越好(很明显协体积相同下,构成正交基的向量最短,想求的最短向量甚至会直接在正交基上!),我们能直接使用LLL算法得到最接近正交基的基底。
流密码
LCG(Linear congruential generator)中文名是“线性同余发生器”,流密码只有一个步骤:异或。
和谁异或呢?这里的LCG就可以生成随机数,实现也非常简单:
就是这么简单,所以现在知道为什么给定种子\(X_0\)的情况下,生成的随机数是相等的吧~
RSA
相邻的pq
如果素数pq直接就是挨着生成的(q=gmpy2.next_prime(p)),通常情况差值都不会超过1000。
那么N的几何平均值s自然是落入pq之间的,就能得到q。
费马分解
如果是q=gmpy2.next_prime(p-r),在我们不能遍历r的情况下,为了找到一个能夹在r范围里的q,我们只知道p-q“比较小”,那么\(\frac{(p-q)^2}{4}=\frac{(p+q)^2}{4} - n\),其中\(\frac{p+q}{2}\)又和N的几何平均值差不多。所以我们能从N的几何平均值开始遍历,看\(s^2-n\)是不是平方数就能解出来。
e和phi不互素
不互素导致没有私钥逆元d。
如果没有填充,明文m比较小,可能可以在“不需要私钥”的情况下直接求解(没有丢失信息),比如n=pqr,但是我们可以把它当作n=pq来看待。
如果 e=e^k导致的和phi不互素,可以把e^k 看做整体来处理,最后明文通过取k次方即可,相当于\((m^k)^e \equiv c\),但是很明显,如果m^k超过n导致丢失信息就不行。
Rabin攻击(e=2)
Rabin加密的时候,由于没有私钥d,所以只能从2次方的性质入手:\(c^{\frac{p-1}{2}}\equiv 1 \pmod p\)
对于 \(m^2 \equiv c \pmod{p}\) 来说,c是模 p 的二次剩余,即: \(c^{\frac{p-1}{2}} \equiv 1 \pmod{p}\)
带入原式得:\(m^2 \equiv c \equiv c^{\frac{p-1}{2}} \cdot c \equiv c^{\frac{p+1}{2}} \pmod{p}\)
所以,为了满足欧拉准则中互质的要求,我们只能把N拆开成pq,最后通过中国剩余定理缝回去。
又因为一个数的平方根有两个,所以一个N=pq能分出四个解:
\(
\begin{cases}
m_1 \equiv c^{\frac{p+1}{4}} \pmod p \\
m_2 \equiv (p - c^{\frac{p+1}{4}}) \pmod p
\end{cases}
\)
def rabin_attack(c, p, q):
n = p * q
c1 = pow(c, (p + 1) // 4, p)
c2 = pow(c, (q + 1) // 4, q)
cc1 = p - c1
cc2 = q - c2
# 下面通过中国剩余定理缝起来
other_except_p = n // p
other_except_q = n // q
p_cancel_other = inverse(other_except_p, p)
q_cancel_other = inverse(other_except_q, q)
m1 = (c1 * p_cancel_other * other_except_p + c2 * q_cancel_other * other_except_q) % n
m2 = (c1 * p_cancel_other * other_except_p + cc2 * q_cancel_other * other_except_q) % n
m3 = (cc1 * p_cancel_other * other_except_p + c2 * q_cancel_other * other_except_q) % n
m4 = (cc1 * p_cancel_other * other_except_p + cc2 * q_cancel_other * other_except_q) % n
return m1, m2, m3, m4
AMM算法(有限域内开根号)
上面的方法都涉及到一个核心问题:当没有私钥d的时候,如何处理进行了e次方的m:\(m^e\)。
Rabin算法是幸运的,\(c^{\frac{p+1}{4}}\)总是能被构造的p=4k+3满足,但如果p不是特别构造的呢?反而使每个\(\phi(p)\)都和e不互素怎么办?
先用\(m^2\equiv c\)举例,我们使用\(p-1=2^ts\)对二次剩余\(x\)进行转换:\(x^{\frac{p-1}{2}} \equiv x^{2^{t-1} * s} \equiv 1 \pmod{p}\)
那我们现在就只需要思考一件事,怎么把\(x^{2^{t-1}s}\)变成\(x^s \equiv 1\),那么我就能\(c^{\frac{s+1}{2}}\equiv c^{\frac{1}{2}}\),自然就得到\(m \equiv c^{\frac{1}{2}}\)。
很好(๑•̀ㅂ•́)و✧,让我们进行第一步消掉t,看到它是\(2^t\)形式,自然是用开平方来解决,但是别忘了有二次剩余和非剩余:
对二次非剩余\(y\):
如果\(x^{2^{t-2} * s} \equiv -1\)岂不是开方失败了?别担心,我们有个天然的-1可以方便的加进等式:
\(x^{2^{t-2} * s} y^{2^{t-2} * s *k} \equiv 1\),这里的k只是像个“开关”一样,用来控制是否启用二次非剩余来校正的。
那一次类推,每次失败了就把k=1打开,召唤二次非剩余来校正我:\(x^{s} y^{s*(2k_1+2^2k_2+...+2^{t-2}k_{t-1})} \equiv 1\)。
那再按照相同的步骤:\(x^{\frac{s+1}{2}} y^{s*(k_1+2^k_2+...+2^{t-3}k_{t-1})} \equiv x^\frac{1}{2}\),将x=c代入即可!
我们知道二次方都有两个解,另一个解直接用p-x即可得到,但是为什么呢?其实是因为另一个解\(-x \% p =p-x\),而另一方面由于费马小定理,±1可以表示为\(x^{\frac{p-1}{2}}\),那么另一个解-m就可以通过随机取有限域p内的数得到:\((m_0*X^{\frac{p-1}{2}})^2 \equiv m_0^2\)。
高次方就没有二次剩余了,看不懂,请参考。
def onemod(e, q):
p = random.randint(1, q-1)
while(powmod(p, (q-1)//e, q) == 1): # (r,s)=1
p = random.randint(1, q)
return p
def AMM_rth(o, r, q): # r|(q-1
assert((q-1) % r == 0)
p = onemod(r, q)
t = 0
s = q-1
while(s % r == 0):
s = s//r
t += 1
k = 1
while((s*k+1) % r != 0):
k += 1
alp = (s*k+1)//r
a = powmod(p, r**(t-1)*s, q)
b = powmod(o, r*a-1, q)
c = powmod(p, s, q)
h = 1
for i in range(1, t-1):
d = powmod(int(b), r**(t-1-i), q)
if d == 1:
j = 0
else:
j = (-math.log(d, a)) % r
b = (b*(c**(r*j))) % q
h = (h*c**j) % q
c = (c*r) % q
result = (powmod(o, alp, q)*h)
return result
def ALL_Solution(m, q, rt, cq, e):
mp = []
for pr in rt:
r = (pr*m) % q
# assert(pow(r, e, q) == cq)
mp.append(r)
return mp
def calc(mp, mq, e, p, q):
i = 1
j = 1
t1 = invert(q, p)
t2 = invert(p, q)
for mp1 in mp:
for mq1 in mq:
j += 1
if j % 100000 == 0:
print(j)
ans = (mp1*t1*q+mq1*t2*p) % (p*q)
if check(ans):
return
return
def check(m):
try:
a = long_to_bytes(m)
if b'CTF' in a:
print(a)
return True
else:
return False
except:
return False
def ALL_ROOT2(r, q): # use function set() and .add() ensure that the generated elements are not repeated
li = set()
while(len(li) < r):
p = powmod(random.randint(1, q-1), (q-1)//r, q)
li.add(p)
return li
cp = c % p
cq = c % q
mp = AMM_rth(cp, e, p) # AMM算法得到一个解
mq = AMM_rth(cq, e, q)
rt1 = ALL_ROOT2(e, p) # 得到所有的ri,即(ri*mp)^e%p = 1
rt2 = ALL_ROOT2(e, q)
amp = ALL_Solution(mp, p, rt1, cp, e) # 得到所有的mp
amq = ALL_Solution(mq, q, rt2, cq, e)
calc(amp, amq, e, p, q) # 俩俩CRT
或者用sagemath,毕竟本质就是解方程,然后用CRT逐个拼回去:
from Crypto.Util.number import *
P.<x> = PolynomialRing(Zmod(p))
f = x ^ 1009 - c
pp = f.roots()
P.<x> = PolynomialRing(Zmod(q))
f = x ^ 1009 - c
qq = f.roots()
for ppp in pp:
for qqq in qq:
tmp_p = int(ppp[0])
tmp_q = int(qqq[0])
m = CRT([tmp_p, tmp_q], [p, q])
if b'CTF' in long_to_bytes(int(m)):
print(long_to_bytes(int(m)))
break
小e(低加密指数)
直接遍历(其实感觉看到某个数“小”的时候都是这样处理的):
for k in range(10000):
m_e = c + k * n
m = iroot(m_e, e)
if m[1]:
print(long_to_bytes(m[0]))
break
广播攻击(相同e)
之所以要求要小e,是因为e如果太大了,可能计算量太大开不出e次方。
因为相同e,所以相同\(m^e\),然后用中国剩余定理把它们拼在一起就可以了。
线性填充广播攻击
很明显还是用中国剩余定理拼在一起,但是要用高科技Sagemath来帮我们解线性多项式了:
Fs = []
for i in range(cnt):
PR.<x> = PolynomialRing(Zmod(Ns[i]))
f = (A[i]*x + B[i])^e - Cs[i] # 填入多项式方程
f = f.monic()
f = f.change_ring(ZZ) # 统一转入ZZ整数域
Fs.append(f)
F = crt(Fs, Ns) # sagemath自带去拼凑多项式中国剩余定理
M = reduce(lambda x, y: x * y, Ns) # 把所有模数乘在一起
FF = F.change_ring(Zmod(M)) # 将结果转入该模数
m = FF.small_roots()
print(long_to_bytes(int(m[0])))
小d
Wiener攻击(连分数近似)
仅在\(d<\frac{1}{3}N^{\frac{1}{4}}\)时生效。
勒让德定理:\(\left\lvert\,f - \frac a b\right\rvert< \frac 1 {2b^2}\)
我们已知:\(ed - k\varphi(N) = 1\),两边同时除以 \(d\varphi(N)\) 得到:\(\frac{e}{\varphi(N)} - \frac{k}{d} = \frac{1}{d\varphi(N)}\),那么对\(\frac{e}{N}\)展开也许就能覆盖到我们想要的\(\frac{k}{d}\)。
def continued_fraction(nm:int,dn:int)->list:
cf=[]
a=nm//dn
r=nm%dn
cf.append(a)
while r!=0:
nm,dn=dn,r
a=nm//dn
r=nm%dn
cf.append(a)
return cf
def fraction_convergent(cf:list)->(int,int):
p=[0,1]
q=[1,0]
i=2
for an in cf:
pn=an*p[i-1]+p[i-2]
qn=an*q[i-1]+q[i-2]
p.append(pn)
q.append(qn)
i+=1
yield pn,qn
def wiener_attack(e:int,N:int)->tuple[bool,int,int]:
cf=continued_fraction(e,N)
cvg=fraction_convergent(cf)
for k,d in cvg:
m=long_to_bytes(pow(c,d,n))
if b'CTF' in m:
print(m)
break
wiener_attack(e,n)
扩展维纳攻击(模版n=2或3)
介绍文章
⚠️被密码学拖很久了,此处等待施工⚠️
🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧🚧
boneh-durfee攻击(界更大)
能到\(d<n^{0.29}\)。
我们有\(ed = 1 + k\varphi(n)\),即\(k(n - p - q + 1) + 1 \equiv 0 \pmod{e}\),\(2k(\frac{n+1}{2} - \frac{p+q}{2}) + 1 \equiv 0 \pmod{e}\)
此时设 \(x = k, y = -\frac{p+q}{2}\),则我们得到了一个模c意义下的二元多项式:\(f(x, y) = 2x(\frac{n+1}{2} + y) + 1 \bmod{e}\)
from Crypto.Util.number import *
N=
e=
c=
"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = False
"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False
"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension
############################################
# Functions
##########################################
# display stats on helpful vectors
def helpful_vectors(BB, modulus):
nothelpful = 0
for ii in range(BB.dimensions()[0]):
if BB[ii, ii] >= modulus:
nothelpful += 1
print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")
# display matrix picture with 0 and X
def matrix_overview(BB, bound):
for ii in range(BB.dimensions()[0]):
a = ('%02d ' % ii)
for jj in range(BB.dimensions()[1]):
a += '0' if BB[ii, jj] == 0 else 'X'
if BB.dimensions()[0] < 60:
a += ' '
if BB[ii, ii] >= bound:
a += '~'
print(a)
# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
# end of our recursive function
if current == -1 or BB.dimensions()[0] <= dimension_min:
return BB
# we start by checking from the end
for ii in range(current, -1, -1):
# if it is unhelpful:
if BB[ii, ii] >= bound:
affected_vectors = 0
affected_vector_index = 0
# let's check if it affects other vectors
for jj in range(ii + 1, BB.dimensions()[0]):
# if another vector is affected:
# we increase the count
if BB[jj, ii] != 0:
affected_vectors += 1
affected_vector_index = jj
# level:0
# if no other vectors end up affected
# we remove it
if affected_vectors == 0:
# print("* removing unhelpful vector", ii)
BB = BB.delete_columns([ii])
BB = BB.delete_rows([ii])
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii - 1)
return BB
# level:1
# if just one was affected we check
# if it is affecting someone else
elif affected_vectors == 1:
affected_deeper = True
for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
# if it is affecting even one vector
# we give up on this one
if BB[kk, affected_vector_index] != 0:
affected_deeper = False
# remove both it if no other vector was affected and
# this helpful vector is not helpful enough
# compared to our unhelpful one
if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(
bound - BB[ii, ii]):
# print("* removing unhelpful vectors", ii, "and", affected_vector_index)
BB = BB.delete_columns([affected_vector_index, ii])
BB = BB.delete_rows([affected_vector_index, ii])
monomials.pop(affected_vector_index)
monomials.pop(ii)
BB = remove_unhelpful(BB, monomials, bound, ii - 1)
return BB
# nothing happened
return BB
"""
Returns:
* 0,0 if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""
def boneh_durfee(pol, modulus, mm, tt, XX, YY):
"""
Boneh and Durfee revisited by Herrmann and May
finds a solution if:
* d < N^delta
* |x| < e^delta
* |y| < e^0.5
whenever delta < 1 - sqrt(2)/2 ~ 0.292
"""
# substitution (Herrman and May)
PR.<u,x,y> = PolynomialRing(ZZ)
Q = PR.quotient(x * y + 1 - u) # u = xy + 1
polZ = Q(pol).lift()
UU = XX * YY + 1
# x-shifts
gg = []
for kk in range(mm + 1):
for ii in range(mm - kk + 1):
xshift = x ^ ii * modulus ^ (mm - kk) * polZ(u, x, y) ^ kk
gg.append(xshift)
gg.sort()
# x-shifts list of monomials
monomials = []
for polynomial in gg:
for monomial in polynomial.monomials():
if monomial not in monomials:
monomials.append(monomial)
monomials.sort()
# y-shifts (selected by Herrman and May)
for jj in range(1, tt + 1):
for kk in range(floor(mm / tt) * jj, mm + 1):
yshift = y ^ jj * polZ(u, x, y) ^ kk * modulus ^ (mm - kk)
yshift = Q(yshift).lift()
gg.append(yshift) # substitution
# y-shifts list of monomials
for jj in range(1, tt + 1):
for kk in range(floor(mm / tt) * jj, mm + 1):
monomials.append(u ^ kk * y ^ jj)
# construct lattice B
nn = len(monomials)
BB = Matrix(ZZ, nn)
for ii in range(nn):
BB[ii, 0] = gg[ii](0, 0, 0)
for jj in range(1, ii + 1):
if monomials[jj] in gg[ii].monomials():
BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU, XX, YY)
# Prototype to reduce the lattice
if helpful_only:
# automatically remove
BB = remove_unhelpful(BB, monomials, modulus ^ mm, nn - 1)
# reset dimension
nn = BB.dimensions()[0]
if nn == 0:
print("failure")
return 0, 0
# check if vectors are helpful
if debug:
helpful_vectors(BB, modulus ^ mm)
# check if determinant is correctly bounded
det = BB.det()
bound = modulus ^ (mm * nn)
if det >= bound:
# print("We do not have det < bound. Solutions might not be found.")
# print("Try with highers m and t.")
if debug:
diff = (log(det) - log(bound)) / log(2)
# print("size det(L) - size e^(m*n) = ", floor(diff))
if strict:
return -1, -1
else:
print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")
# display the lattice basis
if debug:
matrix_overview(BB, modulus ^ mm)
# LLL
if debug:
print("optimizing basis of the lattice via LLL, this can take a long time")
BB = BB.LLL()
if debug:
print("LLL is done!")
# transform vector i & j -> polynomials 1 & 2
if debug:
print("looking for independent vectors in the lattice")
found_polynomials = False
for pol1_idx in range(nn - 1):
for pol2_idx in range(pol1_idx + 1, nn):
# for i and j, create the two polynomials
PR.<w,z> = PolynomialRing(ZZ)
pol1 = pol2 = 0
for jj in range(nn):
pol1 += monomials[jj](w * z + 1, w, z) * BB[pol1_idx, jj] / monomials[jj](UU, XX, YY)
pol2 += monomials[jj](w * z + 1, w, z) * BB[pol2_idx, jj] / monomials[jj](UU, XX, YY)
# resultant
PR.<q> = PolynomialRing(ZZ)
rr = pol1.resultant(pol2)
# are these good polynomials?
if rr.is_zero() or rr.monomials() == [1]:
continue
else:
# print("found them, using vectors", pol1_idx, "and", pol2_idx)
found_polynomials = True
break
if found_polynomials:
break
if not found_polynomials:
# print("no independant vectors could be found. This should very rarely happen...")
return 0, 0
rr = rr(q, q)
# solutions
soly = rr.roots()
if len(soly) == 0:
# print("Your prediction (delta) is too small")
return 0, 0
soly = soly[0][0]
ss = pol1(q, soly)
solx = ss.roots()[0][0]
#
return solx, soly
delta = .271 # this means that d < N^delta
m = 8 # size of the lattice (bigger the better/slower)
t = int((1 - 2 * delta) * m) # optimization from Herrmann and May
X = 2 * floor(N ^ delta) # this _might_ be too much
Y = floor(N ^ (1 / 2)) # correct if p, q are ~ same size
P.<x,y> = PolynomialRing(ZZ)
A = int((N + 1) / 2)
pol = 1 + x * (A + y)
solx, soly = boneh_durfee(pol, e, m, t, X, Y)
d = int(pol(solx, soly) / e)
print(d)
m = power_mod(c, d, N)
print(long_to_bytes(m))
d泄露(ed推全部)
遍历\(i\in[1,s]\),满足\(a^{2^{i}*t} \equiv 1 \mod(n),a^{2^{i-1}*t} \ne 1 mod(n)\),则\(gcd(a^{2^{i-1}*t} -1,n)\) 就是n的一个非平凡因子
我的理解过程是:
- 首先\(a^{2^{i}*t} \equiv 1 \mod(n)\)只是为了先满足\(ed-1=2^it=\phi(n)=(p-1)(q-1)\)
- 这说明什么?假设\(x=a^{2^{i-1}*t}\),意味着有\(x^2=1 \pmod n\)但是\(x≠1\pmod n\)
- 意味着\((x+1)(x-1)=0 \pmod n\)但是\((x-1)≠0\pmod n\)
- 说明(x-1)不是n的倍数,但是它和(x+1)相乘后却能整除n!
- a怎么找?原文说有一半的a满足,毕竟是二次剩余。
t = e * d - 1
s = 0
while t % 2 == 0:
t = t // 2
s += 1
for i in range(1, s):
c1 = pow(2, pow(2, i) * t, n)
c2 = pow(2, pow(2, i - 1) * t, n)
if c1 == 1 and c2 != 1 and c2 != (-1 % n):
p = GCD(c2 - 1, n)
q = n // p
break
光滑数(多个小质数相乘)
p-1
最后返回的是 p+1,使用的时候我们就p-1,所以叫p-1方法。
因为质数p是由很多个小质数构成的:\(p=q_0q_1...q_n\),如果我们能构造一个S使 gcd(S,n)=p,那不就直接得到p了。
为了保证S=kp,我们知道\(2^{p-1}\equiv 1 \pmod p\),如果在平时的话就只能是p-1,在不知道p的前提下我们猜不出来,但是由于p是用很多小q构成的,那我们就能自己一直乘,直到满足条件为止,那我们有必要也用质数来相乘吗?当然没必要,反正只是为了覆盖所有的p,直接全乘起来就行了,也就是阶乘:\(2^{B!}\equiv 1 \pmod p\)
def pollard_method(n):
a = 2 # a可以是任意数,只是为了使用费马小定理
m = 2 # 阶乘开始的地方
while True:
a = pow(a, m, n)
maybe_p = GCD(a - 1, n)
if maybe_p != 1 and maybe_p != n:
return maybe_p
m += 1
p+1
原理很复杂,用模版即可(pip库也有对应函数:pip 库的 primefac.williams_pp1):
from Crypto.Util.number import *
from gmpy2 import *
from itertools import count
def mlucas(v, a, n):
v1, v2 = v, (v ** 2 - 2) % n
for bit in bin(a)[3:]: v1, v2 = ((v1 ** 2 - 2) % n, (v1 * v2 - v) % n) if bit == "0" else (
(v1 * v2 - v) % n, (v2 ** 2 - 2) % n)
return v1
def primegen(): # 这里是生成随机数,如果有给定primes就不需要这个
yield 2
yield 3
yield 5
yield 7
yield 11
yield 13
ps = primegen() # yay recursion
p = ps.__next__() and ps.__next__()
q, sieve, n = p ** 2, {}, 13
while True:
if n not in sieve:
if n < q:
yield n
else:
next, step = q + 2 * p, 2 * p
while next in sieve:
next += step
sieve[next] = step
p = ps.__next__()
q = p ** 2
else:
step = sieve.pop(n)
next = n + step
while next in sieve:
next += step
sieve[next] = step
n += 2
def ilog(x, b): # greatest integer l such that b**l <= x.
l = 0
while x >= b:
x /= b
l += 1
return l
def attack(n):
for v in count(1):
for p in primegen(): # 使用随机数
e = ilog(isqrt(n), p)
if e == 0:
break
for _ in range(e):
v = mlucas(v, p, n)
g = gcd(v - 2, n)
if 1 < g < n:
return int(g), int(n // g) # g|n
if g == n:
break
仅n相同(共模攻击)
我们希望把c1,c2放在一起:\(c_1^{s_1} c_2^{s_2} \equiv (m^{e_1})^{s_1} (m^{e_2})^{s_2}\equiv m^{e_1 s_1 + e_2 s_2}\equiv m \pmod{n}\),当然,放在一起的前提就是共模(在同一个群下)。
让我们看到\(s_1 e_1 + s_2 e_2 = 1\),很显然,此时我们希望这两e是互质的才行。
_, s1, s2 = gmpy2.gcdext(e1, e2)
m = pow(c1, s1, n) * pow(c2, s2, n) % n
print(long_to_bytes(m))
dp/dq(p/q的另一种形式)
为了使解密更快的方法,\(dp=d \% (p-1)\)。
\(\begin{cases}
c^d \equiv m \equiv m_1 \pmod{p} \\
c^d \equiv m \equiv m_2 \pmod{q}
\end{cases}\)
又因为\(c^d = m_1 + kp\)和\(m_2 \equiv m_1 + kp \pmod{q}\),所以\((m_2 - m_1)p^{-1} \equiv k \pmod{q}\):
\(c^d = m_1 + ((m_2 - m_1)p^{-1} \bmod{q})p\)
invp=inverse(p,q)
m1 = pow(c, dp, p)
m2 = pow(c, dq, q)
m = (((m2 - m1)*invp) % q)*p + m1
少dq(小e)
e的作用当然只有一个,和d结合=1。
\(d_pe=1+k(p-1)\),因为k<e,所以可以直接去遍历k。
for k in range(1, e):
p = (dp * e - 1) // k + 1
if n % p == 0:
break
q = n // p
phi = (p - 1) * (q - 1)
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))
少dq(大e)
其实就是接着上面的思考,如果不能简单遍历k的话,就使用欧拉降幂公式:
\(a^{ed_p}-a \equiv 0 \pmod n\)
但是欧拉降幂是有条件的,比如a互质或者大于n。
test = 2
while True:
a = getPrime(test)
p = GCD(pow(a, e * dp, n) - a, n)
q = n // p
phi = (p - 1) * (q - 1)
d = inverse(e, phi)
m = pow(c, d, n)
if b"CTF" in long_to_bytes(m):
print(long_to_bytes(m))
break
test += 1
证书操作
使用现有库提取,pem就是base64过后的der格式。
from Crypto.Util.number import *
from gmpy2 import *
from Crypto.PublicKey import RSA
rsa = RSA.importKey(open("key.pem", "rb").read())
# print(rsa.n, rsa.d, rsa.p)
c = open("./enc", "rb").read()
c = bytes_to_long(c)
m = rsa._decrypt(c)
print(long_to_bytes(m))
如果证书是破损的,就只能自己手动辨识,示例:
30 (长度: 1) 标记符: 代表ASN.1结构的开始
82 (长度: 1) 长度类型: 代表后面跟着一个双字节长度
025b (长度: 2) 长度: 代表后续内容的总长度为603字节
02 (长度: 1) 类型: 代表整数型
01 (长度: 1) 长度: 代表1字节
00 (长度: 1) 值: 代表整数0
02 (长度: 1) 类型: 代表整数型
81 (长度: 1) 长度类型: 代表后面跟着一个单字节长度
80 (长度: 1) 长度: 代表数据长度为128字节
... (长度: 128) 值: 数据值1
按照 类型-长度-值的方式构成,所以都是02开头,修复的时候要和长度来考察,因为数据中也会有02。
对于长度而言,如果最高位是0(比如40/41),那么其值就是长度。如果最高位是1(比如81/82),后面就代表几字节,比如:82 02 5b,代表长度是0x025b。
先使用base64将PEM转为DER:
from base64 import b64decode
import binascii
s = b64decode(s)
print(binascii.hexlify(s))
然后再对照着02来分组:
- 版本
- 模数 - n
- 加密指数 - e
- 解密指数 - d
- 素因子1 - p
- 素因子2 - q
- 指数1 - dp
- 指数2 - dq
- 系数 - invert(q, p)
- 其他额外信息
Schmidt-Samoa(变种RSA)
选取\(N = p^2\cdot q\)作为公钥,\(d = \text{inv}(N, \varphi(pq))\)作为私钥:
- 加密过程:对于小于pq的明文m,计算\(c = m ^ N \bmod N\)作为密文。
- 解密过程:\(m = c^d \bmod pq\)获得明文。
而pq可以通过\(\gcd(2 ^ {N\cdot d}-2, N)\)获得,相当于前者整除pq,后者是\(p^2q\),GCD自然是pq。
pq = GCD(n, pow(2, n * d, n) - 2)
m = pow(c, d, pq)
print(long_to_bytes(m))
但是为什么呢?为什么明明在\(p^2q\)下加密,却可以在pq下解密呢?
让我们看到\(x^n = y^n \pmod n\),即\((xy^{-1})^n =1 \pmod n\)。
我们定义一个函数\(h(x)=x^n \pmod n\),而\(h(x)=1\)的x我们称其组成一个特别的集合“核”。而论文表示,这个核里面只有两种元素:\(\{1,1+kpq\}\),自然的:
- 如果 \(xy^{-1}=1 \pmod{p^2q}\),即 \(x=y \pmod{p^2q}\),那显然\(x=y \pmod{pq}\)
- 如果 \(xy^{-1}=1+kpq \pmod{p^2q}\),很明显在其因子pq下是成立的。
那我们现在就能说:\(c = m^n \pmod n\),就能搬到有限域pq下解决:\(m^{nd}=m \pmod{pq}\)。
等等,为什么说“核”的结果只有这两个?并且让我们再回想两个概念:
- 元素\(x^{ord(n)}\equiv 1 \pmod n\),其中ord(n)是我们的“阶”。
- 阶还代表集合内元素的个数
文章的Lemma1指出,有一类x的阶是p,也就是\(x^p = 1 \pmod n\),这类x就是1+kpq:\(x^p=(1+kpq)^p=1+(kpq)^p \pmod n\)(这是个二项式定理在模p下的特别版本:\((1+a)^p \equiv 1 + a^p \pmod p\)),所以肯定是成立的。
我们还知道,这个1+kpq的阶是p,那么元素肯定是p-1个。其中1肯定也是被包括在核里的,那么现在核里一共有p个元素。
根据拉格朗日定理,我们知道x的阶只能是\(ord(p^2q)\)的因子,让我们用CRT将\(n=p^2q\)拆开为\(\begin{cases} x^n =1 \pmod{p^2} \\ x^n =1 \pmod{q} \end{cases}\),而其他阶(\(p^2,q,pq\))不满足CRT拆出的两个\(Z_{p^2}和Z_q\),比如阶为\(p^2\)不可能满足\(x^{p^2} \equiv 1 \pmod{p^2}\),我们知道只有\(x^{p(p-1)} \equiv 1 \pmod{p^2}(p^2>p(p-1))\)才满足,以此类推。
实际上,由于\(\begin{cases}
x^n \equiv 1 \pmod n \\
x^{\phi(n)} \equiv 1 \pmod n
\end{cases}→GCD(n,\phi(n))=p\),所以符合条件的阶只能是p的因数,也就是1或者p。
也就是说,只有阶1和阶p的x满足\(x^n=1 \pmod{p^2q}\)。
所以这种变种RSA有什么优点吗?
它的密文空间更大,但是却不影响明文解密(只要m<pq)。
而之所以能在密文空间上多乘一个p,是因为其独特的结构,公钥就是模数,导致其子群只能是质数p的因数。而这样子的子群的生成元恰恰好就是pq的倍数,所以很爽的在pq下任意消消乐,从而使明文使用pq解密却不影响。
关联信息攻击(m2=f(m1))
比如\(m_2=am_1+b\),然后再用相同e/n去加密得到c1和c2:\(\begin{cases}
P(x)=x^e-c_1 \\
Q(x)=(ax+b)^e-c_2
\end{cases}\),很明显m1既满足P也满足Q,那么P和Q肯定有公因式\((x-m_1)\)。
Sagemath就是好用:
from Crypto.Util.number import *
def attack(c1, c2, a, b, e, n):
PR.<x>=PolynomialRing(Zmod(n))
g1 = x^e - c1
g2 = (a*x + b)^e - c2
def gcd(g1, g2):
while g2:
g1, g2 = g2, g1 % g2
return g1.monic()
print(gcd(g1, g2))
return -gcd(g1, g2)[0]
m1 = attack(c1, c2, a, b, 5, n)
flag = long_to_bytes(int(m1))
模多项式方程组求根
以下就是示例,如果多项式的阶不同的话,就要转化为同阶,下面是最简单的方法,直接缺多少就补多少\(x^n\):
e = [3, 3, 5, 5, 5]
cnt = 5
Fs = []
PR.<x> = PolynomialRing(ZZ)
for i in range(5):
f = (A[i]*x + B[i])^e[i] - Cs[i]
f = f.change_ring(Zmod(Ns[i]))
f = f.monic()
f = f.change_ring(ZZ)
Fs.append(f)
F = crt( [Fs[0]*x^2, Fs[1]*x^2, Fs[2], Fs[3], Fs[4]], [Ns[i] for i in range(cnt) ] )
M = reduce(lambda x, y: x * y, Ns)
FF = F.change_ring(Zmod(M))
m = FF.small_roots()
print(long_to_bytes(int(m[0])))
但是上面这种方法没有改变模,也就是说上面这种方法只能求\((n_1n_2n_3n_4n_5)^{\frac{1}{5}}\)内的根,但是如果我们采用这种方法:\(c_i = f_i^3(3) + kn_i\) 后,两边平方我们有 \(f_i^6(x) \equiv 2c_i f_i^3(3) - c_i^2 \pmod{n_i^2}\)。
也就是我们对两边进行平方,然后化简后提升模数的话,就能得到更大的根:\((n_1^2n_2^2n_3n_4n_5)^{\frac{7}{6}}\)
未知短填充攻击(m1和m1+r)
from gmpy2 import *
from Crypto.Util.number import *
def franklinReiter(n,e,r,c1,c2):
R.<X> = Zmod(n)[]
f1 = X^e - c1
f2 = (X + r)^e - c2
return Integer(n-(compositeModulusGCD(f1,f2)).coefficients()[0])
def compositeModulusGCD(a, b):
if(b == 0):
return a.monic()
else:
return compositeModulusGCD(b, a % b)
def CoppersmithShortPadAttack(e,n,C1,C2,eps=1/30):
P.<x,y> = PolynomialRing(ZZ)
ZmodN = Zmod(n)
g1 = x^e - C1
g2 = (x+y)^e - C2
res = g1.resultant(g2) # Sagemath的结式默认删除第一个式子的未知数,即这里最后留下的是y
P.<y> = PolynomialRing(ZmodN)
rres = 0
# 这一步的目的是因为虽然res只包含y,但它还是在二元多项式环空间中,我们提取系数和指数重新生成一个一元多项式
for i in range(len(res.coefficients())):
rres += res.coefficients()[i]*(y^(res.exponents()[i][1]))
diff = rres.small_roots(epsilon=eps)
return int(diff[0])
m = franklinReiter(n, e, r, c1, c2)
print(long_to_bytes(m))
部分恢复整体
仅有m高位
比如隐藏了m的低100位,此处n是1024位,e=3,那么能求的小根是\(log_2^{n^{\frac{1}{3}}}≈300\)多位,那就直接用sagemath:
m = m<<100
print(long_to_bytes(m))
PR.<x> = PolynomialRing(Zmod(n))
f = (m+x)^e - c
res = f.small_roots()
m = int(res[0] + m)
print(long_to_bytes(m))
仅有p高位
经验性来看,要求p已知位数大于\(n^{\frac{9}{32}}\):
ph = p<<100
PR.<x> = PolynomialRing(Zmod(n))
f = ph+x
res = f.small_roots(X=2^100, beta=0.4)
p = int(res[0]) + ph
q = n // p
print(q)
d = inverse_mod(65537, (p-1)*(q-1))
m = power_mod(c, d, n)
print(long_to_bytes(m))
仅有d低位
因为和d相关的公式只有\(ed \equiv 1 \pmod{\varphi(n)}\)即\(ed = 1 + k\phi(n)\),化简得\(ed - 1 = k(n - p - n/p + 1)\)即:\(edp - kp(n - p + 1) + kn = p\)
此时,如果我们得到了 \(d\) 的低位 \(d_i\),假设 \(d_i\) 为 \(\alpha\) 位,则有 \(d \equiv d_i \pmod{2^\alpha}\),所以对上述方程两边同时模 \(2^\alpha\) 得:
而我们又知道 \(ed和k\phi(n)\) 是几乎一样大(就相差 \(i\))的,而这里 \(e\) 很小,而 \(d\) 本身是小于 \(\varphi(n)\) 的,则说明此也很小,甚至我们可以得到他的范围一定在 \([1, e]\) 中,所以我们可以通过爆破的方式得到。
这样方程中的未知数便只剩 \(p\),则我们可以尝试利用 \(\text{sage}\) 的 solve_mod 求解模方程,如果有解,我们则可以得到一个解 \(p = p_l \pmod{2^\alpha}\),此时虽然我们没有直接得到 \(d\),但我们利用 \(d_i\) 得到了 \(p\) 的低阶 \(p_l\),此时我们可以考虑转化为上一题中已知的部分信息来构造模多项式:\(f(x) = 2^\alpha x + p_l \mod{n}\)
则我们利用 \(\text{coppersmith}\) 就可以得到模 \(p\) 下面的一个解 \(p_i\) 满足 \(2^\alpha p_i + p_l = p\),则我们成功对素数进行了因数分解。
这里的X便是指定解的上界,这里我们知道p_h < 2^(nbits//2-kbits),
beta则是\(X<n^\beta\),coppersmith方法要求\(\beta\)要小于0.5才能求解,一般都是0.3~0.4。
from Crypto.Util.number import *
def partial_p(p0, kbits, n):
PR.<x> = PolynomialRing(Zmod(n))
nbits = n.nbits()
f = 2^kbits*x + p0
f = f.monic()
roots = f.small_roots(X=2^(nbits//2-kbits), beta=0.3)
if roots:
x0 = roots[0]
p = gcd(2^kbits*x0 + p0, n)
return int(p)
def find_p(d0, kbits, e, n):
X = var('X') # 定义一个变量
for k in range(1, e+1): # 爆破k
results = solve_mod([e*d0*X - k*X*(n-X+1) + k*n == X], 2^kbits)
for x in results: # 如果有解,便得到了p_l
p0 = ZZ(x[0]) # 注意"运算空间",转换为整数域,不太熟悉的可以直接使用int()转换即可。
p = partial_p(p0, kbits, n)
if p:
return p
d=d&(2**410-1)
e = 7
p = find_p(d, 410, e, n) # 410则是题目泄漏的位数大小,
q = n // p
d = inverse(e, (p-1)*(q-1))
print(long_to_bytes(pow(c, d, n)))
相同d(共解密模数攻击)
DSA
离散对数问题
对于\(y=g^x \pmod p\),怎么解决离散对数问题求x呢?
BSGS大步小步法
令m=√p,x=im+j,则\(y=g^x=g^{im+j}\),变形就是:\(y(g^{-m})^i=g^j\)。
原理就是先用j慢慢生成一半的元素,然后让i去跳着快速寻找。
def bsgs(g, y, p):
m = isqrt(p)+1
S = {powmod(g, j, p): j for j in range(m)} # 计算所有g^j
gs = powmod(g, p - 1 - m, p) # -m = -m % (p-1) = p-1-m
for i in range(m):
if y in S:
return i * m + S[y]
y = y * gs % p
Pollard’s kangaroo算法
F = GF(p)
g = F(g)
y = F(y)
x = discrete_log_lambda(y, g, (2^39, 2^40)) # 这里就是给出上下界
是一种蒙特卡洛随机算法,适合已知x的上下界的时候,比BSGS好很多。
原理简介:有两只袋鼠,驯服袋鼠(tame kangaroo)和野生袋鼠(wild kangaroo),tame从最右端b出发,按照固定跳跃规则,来生成中间结果(其实就是有点像是BSGS)。而我们的wild是从y开始跳的,用同样的跳跃规则向左跳,如果碰撞了,说明\(g^{x+d_{wild}}=g^{b+d_{tame}} \pmod p\)。
好像有点粗糙,但真是这样工作的。
已知k攻击
都是得到k过后去计算私钥x,比如如果k共享的话,就能解方程:\(k=\frac{H(m_1)-H(m_2)}{s_1-s_2}\pmod{q}\)
如果k2=ak1+b这些线性关系也是,将式子合并在一起消掉x后就可以求k了。
比如\(k_2 = k_1^2\),我们有式子\(\begin{cases}
s_1 \equiv (H(m_1) + r_1x)k_1^{-1} \pmod{q} \\
s_2 \equiv (H(m_2) + r_2x)k_2^{-1} \pmod{q}
\end{cases}\),那拼一拼就变成\(s_2k_1^2r_1 - s_1k_1r_2 - H(m_2)r_1 + H(m_1)r_2 \equiv 0\),最后就是\(f = s_2x^2r_1 - s_1xr_2 - H(m_2)r_1 + H(m_1)r_2 \bmod{q}\)放进Sagemath中就能求解了~
from Crypto.Util.number import *
p, q, g, y = ...
(h1, r1, s1) = ...
(h2, r2, s2) = ...
PR.<x> = PolynomialRing(GF(q))
f = s2*x^2*r1 - s1*x*r2 - h2*r1 + h1*r2
print(f.roots())
k = int(f.roots()[1][0]) # 根有两个,自己选一个即可
x = (s1*k - h1) * inverse(r1, q) % q
print(long_to_bytes(x))
格密码
格密码需要习题才更好理解,请记得看我的仓库,用Jupyter-Sagemath写的,很详细。
格构造技巧
有一点必须保证,就是自己计算一次目标向量是否满足Hermite定理。
目前感觉有两个技巧:
- 可以通过在格中自行添加值来决定目标向量的结果
- 不同位置的排列可以有更好的表现,比如抵消未知数
配平
关于第一点,如果你希望目标向量的结果是均匀的,那么就可以配平格。
比如nG-四道练习题的第四题,可以通过人为乘上数值,使得目标向量“扁平化”,不单一依赖于某一特定坐标轴,这种目标向量是更好发现的:
然后再配平一下,目标向量位数为:
那就配平:
但是!如果你的目标向量中已经扁平了(或者想要的目标值远小于其他值),这可能会导致LLL算法不能找出想要的值,此时我们需要“有所偏袒”,人为给我们想要的值一些合理的大值,使得计算出来的目标向量的权重就是我们想要的单一值。
调整位置
如果有不想要的未知数k,如果不想让它出现在目标向量中,有时候将格的位置移动后能去除掉未知数,比如上面的格,如果是这样子,就会导致目标向量出现未知数:
对称密码
分组密码
流密码
流密码能打交道的就一条式子:$$X_{n+1} \equiv aX_{n}+b\pmod m$$
有一道综合题挺有意思,其实就概括流密码的全部考点了。
恢复a/b/m
比如这样子的题,只给生成后的结果不给a/b/m:
我们相减即可得到关系:
根据等比数列的性质:\(t_{i+1}t_{i-1}=t_i^2\):
即可得到:
这意味着\(t_{i+1}t_{i-1}-t_i^2\)是m的倍数,我们能通过不断求解最大公约数筛出m,但是如果给的式子较少的话(比如恢复m最少需要4条),那么m里面可能有很多其他的素数,其实就相当于:\(t_{i+1}t_{i-1}-t_i^2=k_1k_2k_3...k_nm\),里面可能夹杂其他因数。
x = [x1, x2, x3, x4, x5]
t = []
for i in range(1, len(x)):
t.append(x[i] - x[i-1])
m = 0
for i in range(1, len(t)-1):
m = GCD(t[i+1]*t[i-1] - t[i]*t[i], m)
for p in sieve_base: # 筛掉小因数
while m % p == 0: m //= p
assert isPrime(m)
a = (x3 - x2) * inverse(x2 - x1, m) # 然后就能求出a和b
b = (x2 - a*x1) % m
inva = inverse(a, m)
for i in range(2**16):
x1 = (x1-b)*inva % m
flag = long_to_bytes(x1)
if b'NSSCTF' in flag:
print(flag)
Tonelli-Shanks算法
烦捏,这里遇到这个东西了,甚至比AMM还难理解。
让我们回顾什么是二次剩余以及其满足的欧拉准则:
我们现在把p-1分解成\(p-1=Q2^s\),我们可以发现,如果s=1的话意味着\(p \equiv 2Q+1\equiv 2(2k+1)+1 \equiv 4k+3 \pmod p\),是的,这就是Rabin算法,能直接开方的算法,因为我们本来就有\(x\equiv c^{\frac{p+1}{4}}\),只有Rabin能满足指数条件(详情请看上面的Rabin攻击)
现在让我们先定义几个变量:\(\begin{cases} n:我们需要求的二次剩余 \\ z:一个模p下的二次非剩余 \\ c=z^Q :调整因子\\ R=n^{\frac{Q+1}{2}} :初始平方根猜测\\ t=n^Q :检验值\\ m=S:循环控制因数 \end{cases}\),R和t是最好理解的,它就是\(R^2 \equiv n^{Q+1} \equiv n \cdot t\)得来的,如果t=1那不就通过欧拉准则的考验了。m其实就相当于AMM算法中S//=2,c调整因子就像AMM算法中如果“偏离1”就立马乘上给它补回去的值。
这两天学密码学烦了,就这样了,散会!
def legendre(a, p):
return pow(a, (p - 1) // 2, p)
def tonelli(n, p):
assert legendre(n, p) == 1, "not a square (mod p)"
q = p - 1
s = 0
while q % 2 == 0:
q //= 2
s += 1
if s == 1:
return pow(n, (p + 1) // 4, p)
for z in range(2, p):
if p - 1 == legendre(z, p):
break
c = pow(z, q, p)
r = pow(n, (q + 1) // 2, p)
t = pow(n, q, p)
m = s
t2 = 0
while (t - 1) % p != 0:
t2 = (t * t) % p
for i in range(1, m):
if (t2 - 1) % p == 0:
break
t2 = (t2 * t2) % p
b = pow(c, 1 << (m - i - 1), p)
r = (r * b) % p
c = (b * b) % p
t = (t * c) % p
m = i
return r
本文来自博客园,作者:muyiGin,转载请注明原文链接:https://www.cnblogs.com/muyiGin/p/18805438



 浙公网安备 33010602011771号
浙公网安备 33010602011771号