详细介绍：基于遗传优化的LSTM-Attention一维时间序列预测算法matlab仿真

目录

1.前言

2.算法运行效果图预览

3.算法运行软件版本

4.部分核心程序

5.算法仿真参数

6.算法理论概述

7.参考文献

8.算法完整程序工程

---

1.前言

       传统LSTM模型虽能捕捉时序依赖，但存在超参数依赖经验设置、长序列关键信息挖掘不足的问题。基于遗传优化的LSTM-Attention算法通过Attention机制强化关键时序特征的权重，再利用遗传算法（GA）全局优化模型超参数，显著提升了预测精度与鲁棒性。

2.算法运行效果图预览

(完整程序运行后无水印)

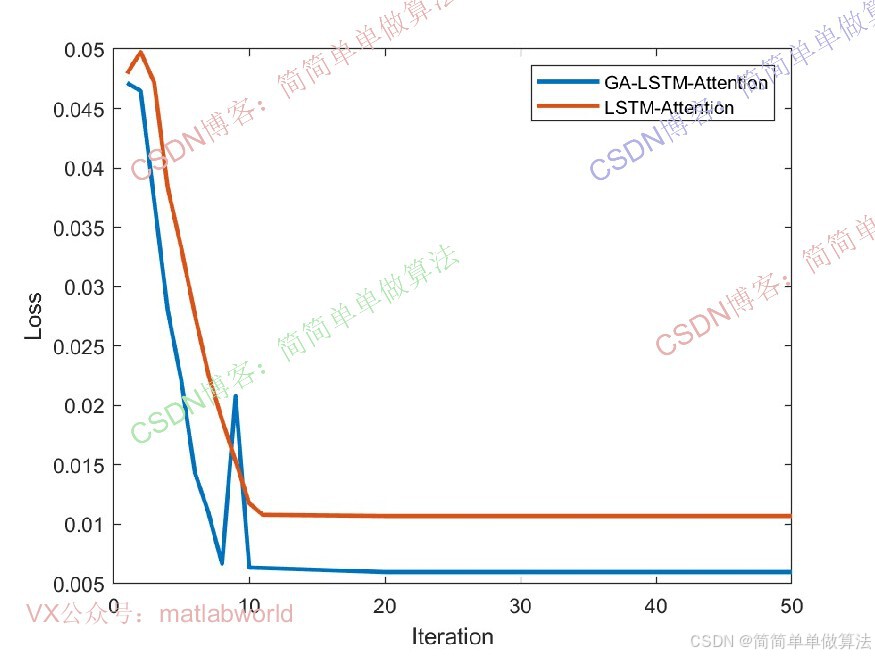
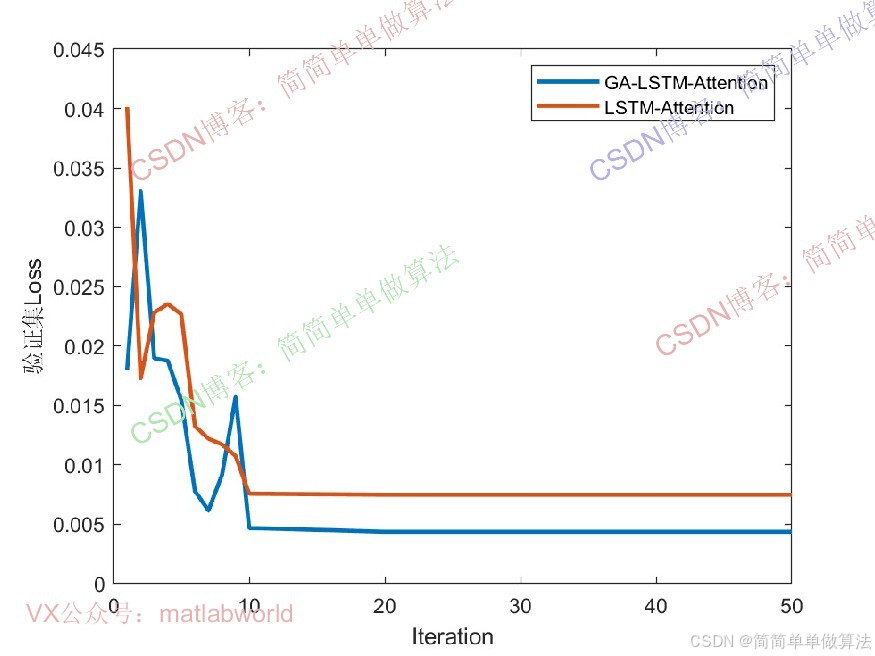
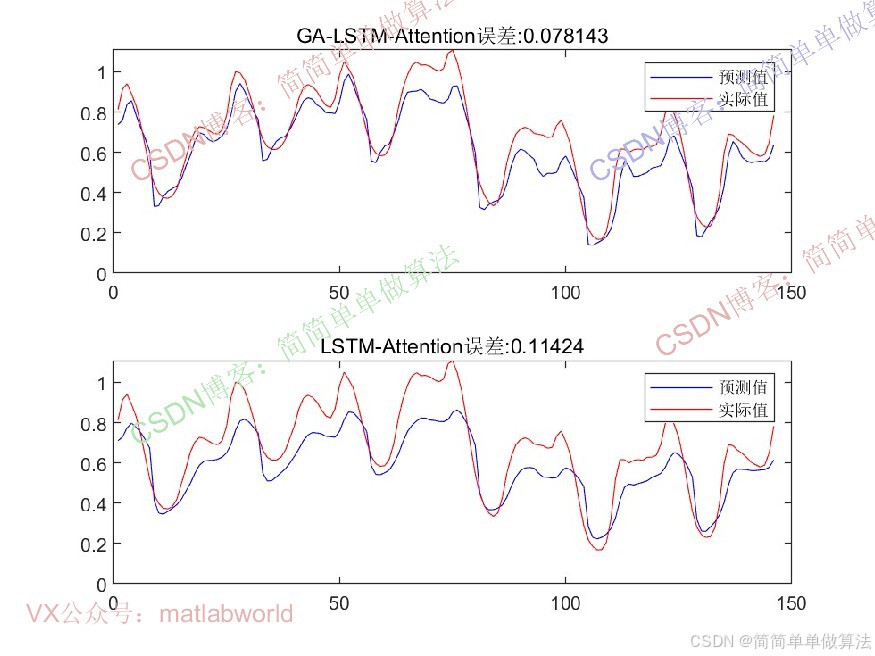
3.算法运行软件版本

Matlab2024b(推荐)或者matlab2022a

4.部分核心程序

（完整版代码包含中文注释和操作步骤视频）

......................................................................
%% 迭代更新
    % batch 更新
    for i = 1 : Epochs
        ij  = ij + 1;
        idx = (i-1)*Bsize+1:i*Bsize;
        dlX = gpuArray(Xtrain(:,idx,:));
        dlY = gpuArray(Ttrain(idx));
        [gradients,loss,state] = dlfeval(@func_Model,dlX,dlY,para,state);
        %L2正则化
        RL2                  = 0.001;
        [para,Gradm,SqGradm] = adamupdate(para,gradients,Gradm,SqGradm,ij,Lr);
        % 验证集测试
        if ij == 1 || mod(ij,Vfre) == 0
            oYnorm = func_Predict(gpuArray(Xnorm),para,Vstate);
            VLOSS  = mse(oYnorm, gpuArray(Ynorm));
        end
    end
    LOSSer  = [LOSSer,loss];
    VLOSSer = [VLOSSer,double(gather(extractdata(VLOSS)))];
    % 每轮epoch 更新学习率
figure
plot(LOSSer,'LineWidth',2);
hold on
plot(VLOSSer,'LineWidth',2);
xlabel("Iteration")
ylabel("Loss")
legend('训练集','验证集')
%预测
Ynpre = func_Predict(gpuArray(Xtest),para,Tstate);
Ynpre = extractdata(Ynpre);
%可视化
figure
plot(Ynpre,'b');
hold on
plot(Ttest,'r')
legend('预测值','实际值')
233

5.算法仿真参数

% 自定义训练循环的深度学习数组
Xtrain    = dlarray(Xtrain,'CBT');
Ttrain    = dlarray(Ttrain,'BC');
Xtest     = dlarray(Xtest,'CBT');
Ttest     = dlarray(Ttest,'BC');
% 训练集和验证集划分
All_Len   = length(Ttrain);
Valid_Len = floor(All_Len * 0.05);
Xnorm     = Xtrain(:,end - Valid_Len:end,:);
Ynorm     = Ttrain(:,end-Valid_Len:end,:);
Xtrain    = Xtrain(:,1:end-Valid_Len,:);
Ttrain    = Ttrain(:,1:end-Valid_Len,:);
% Lr        = 0.01;
% % 学习丢失率
% Lrdf      = 0.0002;
% % 梯度阈值
% Lvl_sgrad = 0.01;

6.算法理论概述

该算法本质是“特征增强（Attention）+ 时序建模（LSTM）+ 参数优化（遗传算法） ”的三层架构，三者协同解决一维时间序列预测的核心痛点：

LSTM层：通过门控机制（输入门、遗忘门、输出门）处理时间序列的长期依赖，避免传统RNN 的梯度消失问题；

Attention层：为LSTM输出的不同时刻特征分配动态权重，突出对预测结果影响显著的关键时序片段（如电力负荷中的 “峰谷时段” 特征）；

遗传优化层：将LSTM-Attention的超参数（如学习率、隐藏层神经元数、Attention权重维度）编码为 “染色体”，通过选择、交叉、变异操作搜索全局最优超参数组合，替代人工调参的盲目性。

       LSTM-Attention 的预测性能高度依赖超参数，如学习率η、LSTM隐藏层神经元数h、Attention 权重维度da​、批大小B等。传统人工调参（如网格搜索）易陷入局部最优，遗传算法通过模拟生物进化过程，实现超参数的全局优化。

       适应度函数是遗传算法的“评价标准”，需与模型预测目标一致（如最小化预测误差）。此处以 “LSTM-Attention在验证集Dval​上的均方根误差（RMSE）的倒数” 作为适应度值，适应度越高，超参数组合越优。其中定义适应度函数为：

       相比传统LSTM，该算法通过Attention机制强化关键时序特征，减少无关信息干扰；通过遗传算法全局优化超参数，避免人工调参的主观性，在长序列、高噪声的一维时间序列（如金融波动、设备振动信号）预测中表现更优。

7.参考文献

[1]汪敏,田大平.改进粒子群算法优化CNN-LSTM-Attention模型在安全生产事故预测中的应用[J].安全与环境学报, 2025(5).

[2]徐丸絮,沈吟东.基于Attention-LSTM神经网络的公交行程时间预测[J].现代电子技术, 2022(003):045.

8.算法完整程序工程

OOOOO

OOO

O

关注后输入自动回复码：0002