[COMP2121] Bertrand's Ballot Problem and Balanced Bracket Sequence

Description

Suppose there are $x$ votes for $A$ and $y$ notes for $B$, and $x>y$. How many sequences are there of revealing the votes such that the number of votes for $A$ is always strictly bigger than that for $B$?

 

Solution (by reflection)

First, we draw the process of revealing the votes using line charts (the horizontal axis represents the number of votes revealed, and the vertical axis represents $x_{cur}-y_{cur}$):

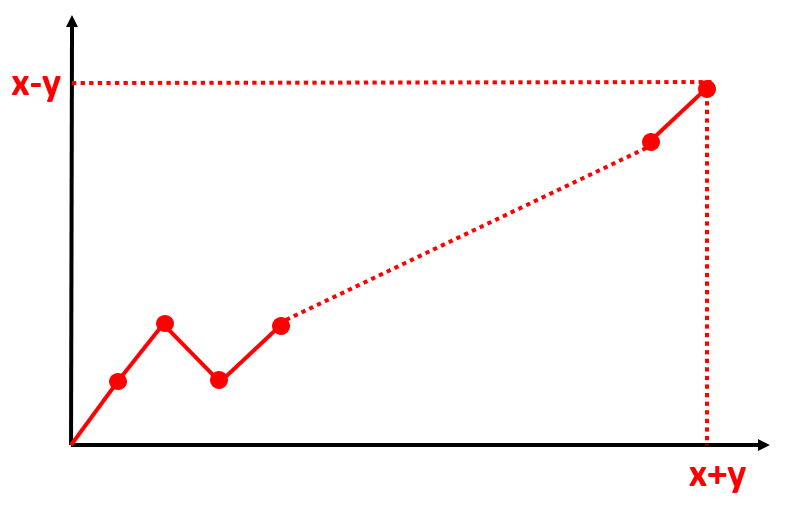
Define the grand set $\Omega$ as the set of sequences that starts from $0$ and ends at $x-y$. A valid sequence drawn in such a way should never touch the horizontal axis. 

Note that the first vote must be a "+1". Let $A$ denote the set of sequences whose first element is "+1" and $B$ denote the set of sequences whose first element is "+1" but not valid (touches 0 at some point). Then the answer would be

$$|A| - |B|$$

It is easy to see that

$$|A| = \frac{(x+y-1)!}{(x-1)!y!}$$

Now use the technique of bijection to compute $|B|$, i.e. find an easily-computable set $C$ so that sequences in $B$ and $C$ have a one-to-one relation.

We attempt to find $C$ in such a way: for every sequence in $B$, reflect the prefix before the line first touches 0 with respect to the horizontal axis to get a sequence in $C$:

By observing, we try to define $C$ to be the set of sequences whose first element is "-1" (and ends at $x-y$). Then, according to the mapping, different sequences in $B$ will result in different sequences in $C$, so the mapping is injective. Also, for every sequence in $C$, a sequence in $B$ is obtained by reflecting $C$'s prefix before first touching 0 (such prefix always exists because it goes from $-1$ to $x-y$), so the mapping is bijective. Therefore, we successfully find the $C$ we want.

Now compute $|C|$. Suppose in the next $x+y-1$ steps, there are $a$ "+1"s and $b$ "-1"s, then:

$$\left\{\begin{matrix}a+b=x+y-1 \\-1+a-b=x-y\end{matrix}\right. \Rightarrow \left\{\begin{matrix}a=x \\b=y-1\end{matrix}\right.$$

Thus,

$$|C|=\frac{(x+y-1)!}{x!(y-1)!}$$

Alternatively, $C$ is the complement of $A$, thus:

$$|C|=|\Omega|-|A|=\frac{(x+y)!}{x!y!}-\frac{(x+y-1)!}{(x-1)!y!}=\frac{(x+y-1)!}{x!(y-1)!}$$

Finally, we can compute the answer:

$$|A|-|B|=|A|-|C|=\frac{(x-y)(x+y-1)!}{x!y!}$$

Moreover, the corresponding probability is:

$$p=\frac{\frac{(x-y)(x+y-1)!}{x!y!}}{\frac{(x+y)!}{x!y!}}=\frac{x-y}{x+y}$$

 

联想：合法括号串（Catalan数）

这两个问题十分相似，区别在于括号串问题中，左括号和右括号的差值可以为0。其实，长度为$2n$的合法括号串数量等于第$n$个 Catalan 数$C_n$，其通项公式也可以用十分相似的方法推导出来。

$A$代表$n$个左括号和$n$个右括号的全部排列，$B$代表其中不合法的括号序列，则答案为：

$$C_n=|A|-|B|$$

不难写出：

$$|A|=\frac{(2n)!}{n!n!}$$

现在考虑计算$|B|$。沿用上述表示，用以下方法将$B$中的序列映射至$C$：将序列$B$截至第一次差为$-1$的前缀进行翻转，即左括号变成右括号，右括号变成左括号，如 (())) 变成 ))(((。假设这样的前缀为$[1,k]$，则$k$必为奇数（若为偶数，则$[1,k-1]$亦满足条件），因此原前缀有$\frac{k-1}{2}$个左括号和$\frac{k+1}{2}$个右括号，因此翻转后，总序列共有$n-\frac{k-1}{2}+\frac{k+1}{2}=n+1$个左括号，$n-\frac{k+1}{2}+\frac{k-1}{2}=n-1$个右括号。那么，$C$即为由$n+1$个左括号和$n-1$个右括号组成的括号串：

$$|C|=\frac{(2n)!}{(n+1)!(n-1)!}$$

考虑是否为单满射。显然满足单射。对于$C$中的每个序列，一定存在一个位置，左括号的数量第一次大于右括号，对截至此位置的前缀进行反转，总可以得到一个不合法的括号串，因此满足满射。因此，$|B|=|C|$。

最后，可以推出：

$$C_n=|A|-|B|=\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n+1)!(n-1)!}=\frac{(2n)!}{n!(n+1)!}$$