机器学习Day003：多元线性回归

多元线性回归尝试通过一个线性方程来适配观测数据，这个线性方程是在两个以上（包括两个）的特征和响应之间构建一个关系。多元线性回归的实现步骤和简单线性回归很相似，在评价部分有所不同。你可以用它来找出预测结果上哪个因素影响力最大，以及不同变量是如何相互关联的。

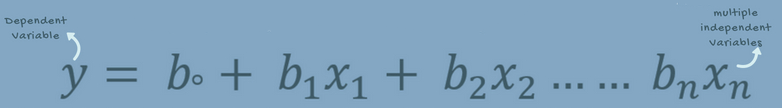
前提

想要有一个成功的回归分析，确认这些假设很重要

1. 线性：自变量和因变量的关系应该是线性的（也即特征值和预测值是线性相关的）

2. 保持误差项的方差齐性（常数方差）：误差项的分散（方差）必须等同

   这句话是关于线性回归模型的一个假设。它的意思是，在给定自变量的条件下，因变量的误差项（也就是真实值和预测值之间的差异）的方差必须是一个常数，而不是随着自变量的变化而变化。这样才能保证线性回归模型的有效性和稳定性。

   方差齐性是指在不同的条件下，某个变量的方差是否相等。例如，如果我们想比较不同年龄段的人的身高，我们就需要检验身高这个变量在不同年龄段中的方差是否相等。如果方差相等，就说明身高的波动程度在不同年龄段中是一致的，那么我们就可以直接比较身高的均值。如果方差不等，就说明身高的波动程度在不同年龄段中是不一致的，那么我们就不能直接比较身高的均值，而需要进行一些校正或者选择其他的方法。

3. 多元正态分布：多元回归假定残差符合正态分布

   这句话是关于多元回归模型的一个假设。它的意思是，多元回归模型中的残差（也就是因变量的真实值和预测值之间的差异）符合多元正态分布。多元正态分布是一种多维的概率分布，它可以描述多个相关的正态变量的联合分布。多元正态分布有两个重要的参数：均值向量和协方差矩阵。均值向量表示每个变量的期望值，协方差矩阵表示每对变量之间的协方差。如果残差符合多元正态分布，那么就说明残差没有系统的偏差，而且残差之间没有相关性。

   残差是观测值和预测值之间的差异。在多元回归模型中，残差是因变量的真实值和模型预测的值之间的差异。例如，如果你用一个模型来预测一个人的身高，而这个人的真实身高是170厘米，而模型预测的身高是165厘米，那么这个人的残差就是170 - 165 = 5厘米。

   残差可以用来评估模型的拟合程度和检验模型的假设。如果残差较小，那么说明模型能够较好地捕捉数据中的主要变化和规律，而且误差是随机的。如果残差较大，那么说明模型不能够很好地拟合数据，或者存在一些系统的偏差或相关性。我们可以用残差图来直观地观察残差的分布和特征。

   协方差矩阵是一个描述多个变量之间协方差的矩阵。协方差是一个衡量两个变量之间线性相关程度的指标，它的公式是：

   Cov(X, Y) = E[(X - E[X])(Y - E[Y])]

   其中E[X]和E[Y]分别是X和Y的期望值。如果Cov(X, Y) > 0，那么就说明X和Y有正相关性；如果Cov(X, Y) < 0，那么就说明X和Y有负相关性；如果Cov(X, Y) = 0，那么就说明X和Y没有线性相关性。

   协方差矩阵的对角线元素是每个变量自身的方差，也就是变量的波动程度。协方差矩阵的非对角线元素是每对变量之间的协方差。例如，如果有三个变量X1，X2和X3，它们的协方差矩阵是：

   [Var(X1) Cov(X1, X2) Cov(X1, X3)
   Cov(X2, X1) Var(X2) Cov(X2, X3)
   Cov(X3, X1) Cov(X3, X2) Var(X3)]

4. 缺少多重共线性：假设数据有极少甚至没有多重共线性。当特征（或自变量）不是相互独立时，会引发多重共线性。

   这句话是关于多元回归模型的一个假设。它的意思是，多元回归模型中的自变量（或特征）之间没有或者很少有线性相关性。如果自变量之间存在较强的线性相关性，那么就会引发多重共线性的问题。多重共线性是指在多元回归模型中，一个或多个自变量可以用其他自变量的线性组合来近似表示。

   多重共线性会影响模型的稳定性和可信度。如果存在多重共线性，那么模型的参数估计就会不准确，标准误就会增大，置信区间就会扩大，检验统计量就会失效。这样就会导致我们无法判断每个自变量对因变量的影响有多大，以及哪些自变量是多余的。

虚（拟）变量

在多元回归模型中，当遇到数据集是非数值数据类型时，使用分类数据是一个非常有效得方法。

分类数据，是指反映（事物）类别的数据，是离散数据，其数值个数（分类属性）有限（但可能很多）且值之间无序。比如，按性别分为男、女两类。在一个回归模型中，这些分类值可以用虚变量来表示，变量通常取诸如0或1这样的值，来表示肯定类型或否定类型。

虚拟变量陷阱

虚拟变量陷阱是指两个以上（包括两个）变量之间高度相关的情形。简而言之，就是存在一个能够被其他变量预测出的变量。我们举一个存在重复类别（变量）的直观例子：假使我们舍弃男性性别，那么该类别也可以通过女性类别来定义（女性值为0是表示男性，为1，表示女性），反之，亦然。

解决虚拟陷阱的方法是，类别变量减去一：加入有m个类别，那么在模型构建时取m-1个虚拟变量，减去的那个变量可以看作是参照值。

这段话是关于虚拟变量陷阱的一个解释。虚拟变量是一种用来表示类别变量的方法，它把每个类别用一个0或1的值来表示。例如，如果有一个性别变量，它有两个类别：男性和女性，那么我们可以用一个虚拟变量来表示，它的值为0表示男性，为1表示女性。

虚拟变量陷阱是指当我们使用多个虚拟变量来表示一个类别变量时，可能会出现完全或者近似的多重共线性的问题。也就是说，一个或多个虚拟变量可以用其他虚拟变量的线性组合来表示。这会导致模型的参数估计不准确或者不稳定。

例如，如果我们用两个虚拟变量来表示性别变量，分别为X1和X2，它们的值如下：

X1 X2 性别
0 0 男性
0 1 女性
1 0 男性
1 1 女性

那么我们可以看出，X1和X2之间存在完全的多重共线性，因为它们的值完全相同。这意味着X1和X2之间有一个完全的线性关系，它们可以互相预测对方。这样就会造成虚拟变量陷阱。

解决虚拟变量陷阱的方法是，只使用m-1个虚拟变量来表示一个有m个类别的变量，其中一个类别作为参照类别。例如，如果我们只用一个虚拟变量X来表示性别变量，它的值为0表示男性，为1表示女性，那么我们就可以避免虚拟变量陷阱。这样做的原理是，当我们知道了m-1个类别的情况时，就可以推断出第m个类别的情况。

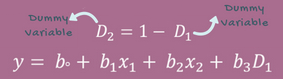
注意

过多的变量可能会降低模型的精确度，尤其是如果存在一些对结果无关的变量，或者存在对其他变量造成很大影响的变量时。这里介绍一些选择合适变量的方法：

1. 向前选择法
2. 向后选择法（也称 向后剔除法/向后消元法）
3. 向前向后法：即结合了上面说的向前法和向后法，先用向前法筛选一遍，再用向后法筛选一遍，知道最后无论怎么筛选模型变量都不再发生变化，就算是结束了

这段话是关于多元回归模型中的变量选择的一个介绍。变量选择是指在多个自变量中选择一部分最合适的变量来构建模型的过程。变量选择的目的是为了提高模型的精确度和解释力，避免过拟合和多重共线性等问题。这里介绍了三种常用的变量选择方法：

• 向前选择法：这种方法是从没有任何自变量的模型开始，逐步添加自变量，每次添加对模型改进最大的自变量，直到没有任何自变量可以显著改进模型为止。

• 向后选择法：这种方法是从包含所有自变量的模型开始，逐步删除自变量，每次删除对模型改进最小的自变量，直到没有任何自变量可以删除而不显著损害模型为止。

• 向前向后法：这种方法是结合了向前选择法和向后选择法，先用向前选择法筛选一遍，再用向后选择法筛选一遍，反复进行，直到最后无论怎么筛选模型变量都不再发生变化为止。

Step 1：数据预处理

导入相关库

import pandas as pd
import numpy as np

导入数据集

dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[ : , :-1].values
Y = dataset.iloc[ : ,  4 ].values

将类别数据数字化

from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[: , 3] = labelencoder.fit_transform(X[ : , 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()

一个已经废弃的参数categorical_features。这个参数是用来指定哪些列是类别变量的，但是在sklearn的1.0版本中，它已经被移除了。你可以使用ColumnTransformer类来代替它，它可以让你对不同的列应用不同的转换器。例如，如果你想对第四列进行独热编码，你可以这样写：

from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer
ct = ColumnTransformer(
[("onehot", OneHotEncoder(), [3])], # 对第四列（索引为3）进行独热编码
remainder="passthrough" # 保留其他列
)
X = ct.fit_transform(X)

这段代码是用来对一个数据集中的类别变量进行编码的。类别变量是指有固定类别的变量，例如性别，国家，颜色等。编码的目的是为了把类别变量转换成数值变量，以便于进行数学运算和建模。这段代码使用了sklearn库中的两个编码器：LabelEncoder和OneHotEncoder。

LabelEncoder是一种用来把类别变量转换成整数标签的编码器。它会给每个类别分配一个唯一的整数值，从0开始。例如，如果有一个性别变量，它有两个类别：男性和女性，那么LabelEncoder会把男性编码为0，女性编码为1。

OneHotEncoder是一种用来把类别变量转换成一维数组的编码器。它会给每个类别创建一个新的列，并用0或1来表示该类别是否出现。例如，如果有一个国家变量，它有三个类别：中国，美国和日本，那么OneHotEncoder会创建三个新的列，并用以下方式表示：

国家 中国 美国 日本
中国 1 0 0
美国 0 1 0
日本 0 0 1

这段代码的具体步骤如下：

• 首先导入sklearn库中的LabelEncoder和OneHotEncoder。

• 然后创建一个LabelEncoder对象，并用它对数据集中的第四列（索引为3）进行编码。这里假设第四列是一个类别变量，例如国家。

• 接着创建一个OneHotEncoder对象，并指定对第四列进行独热编码。这里使用了categorical_features参数来指定哪些列是类别变量。

• 然后用OneHotEncoder对象对数据集进行编码，并把结果转换成一个数组。这里使用了fit_transform方法来同时拟合和转换数据集。

躲避虚拟变量陷阱

X = X[: , 1:]

最后把数组中的第一列（索引为0）删除，因为它是多余的。这里使用了切片操作来删除第一列。

数组中的第一列（索引为0）是多余的，是因为它会导致多重共线性的问题。多重共线性是指在多元回归模型中，一个或多个自变量可以用其他自变量的线性组合来近似表示。这会影响模型的参数估计和检验的准确性和可信度。

在这段代码中，第四列（索引为3）是一个类别变量，例如国家。使用OneHotEncoder对它进行编码后，会生成三个新的列，分别表示中国，美国和日本。这三个列之间存在完全的多重共线性，因为它们的值完全相反。例如，如果一个观测值是中国，那么它的编码就是[1, 0, 0]；如果是美国，就是[0, 1, 0]；如果是日本，就是[0, 0, 1]。这样就可以看出，任何一个列都可以用其他两个列的线性组合来表示。例如，第一列（索引为0）就等于1减去第二列（索引为1）和第三列（索引为2）之和。

为了避免多重共线性的问题，我们可以删除其中一个列，把它作为参照类别。这样做的原理是，当我们知道了其他两个类别的情况时，就可以推断出第三个类别的情况。例如，如果我们删除第一列（索引为0），那么当我们看到[0, 1, 0]时，就知道它表示美国；当我们看到[0, 0, 1]时，就知道它表示日本；当我们看到[0, 0, 0]时，就知道它表示中国。

源码是对第四列进行类别编码，但是编码后的结果会插入到原来的数据集中，而不是替换第四列（但会将第4列删除）。也就是说，编码后的数据集会有三列多出来，分别是第一列（索引为0），第二列（索引为1）和第三列（索引为2）。这三列就是对第四列进行独热编码后的结果。因此，第一列是多余的，因为它会和第二列和第三列产生多重共线性。

拆分数据集为训练集和测试集

from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state = 0)

Step 2：在训练集上训练多元线性回归模型

from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, Y_train)

Step 3：在测试集上预测结果

y_pred = regressor.predict(X_test)