(1)ReLU及其扩展
ReLU (Rectified Linear Unit),整流线性单元:
![]()
ReLU由于和线性单元非常类似,因此比较容易优化:一是其一阶导大且一致,二是其二阶导数几乎处处为0。但是ReLU也有一些问题,它不能通过基于梯度的方法学习那些使它们激活为0的样例。具体来说,若经过激活函数后其值为0,该部分的导数也为0,会使得该神经元一直处于dead的状态。ReLU的各个扩展也是为了解决这个问题。
ReLU的三个扩展基于当zi<0时使用一个非零的斜率。
- 绝对值整流 (absolute value rectification):
![]()
- 渗漏ReLU (Leaky ReLU):
![]()
- 参数化ReLU (parametric ReLU):
将渗漏ReLU中的0.01视为变量在训练中不断学习。
-maxout:
maxout进一步扩展了ReLU。对于原本的激活函数,简单起见我们假设原本的网络的第i层如下所示:
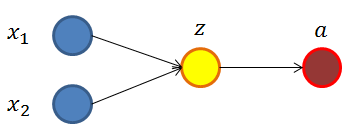
传统的输出计算公式是:
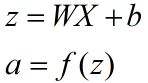
f为激活函数,如sigmoid,ReLU,Tanh等。
对于maxout方法,若我们设置maxout的参数k=3,则该层的构造如下图所示:

此时maxout网络的输出计算公式为:

因此使用maxout作为激活层的时候,参数个数会成k倍增加。
maxout单元可以学习具有多大k段的分段线性的凸函数。maxout继承ReLU的优点并避免了ReLU的缺点。
因为每个单元由多个过滤器驱动,maxout具有一些冗余来帮助它们抵抗一种被成为灾难遗忘的现象,这个现象是说神经网络忘记了如何执行它们过去训练的任务。
(2) logistic sigmoid与正曲双切函数
早期神经网络使用的激活函数,在此就不做赘述了。渐渐不使用的主要原因就是其容易饱和导致梯度弥散。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号