如何输入数学公式--兼论LaTex语法
使用LaTex可以生成复杂的数学公式。
在启明星数学系统里，使用“$”和"$" 包裹的是行内公式， 使用 "$$"和 "$$" 是段落公式。
所谓行内公式就是 文字和公式在一行里。
而所谓段落公式就是 公式另起一行。
之所以有段落公式是因为，有些公式很复杂，在一行里显示的效果并不好
举例：
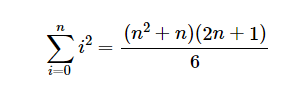
他的数学公式就是
$$ \sum_{i=0}^n i^2 = \frac{(n^2+n)(2n+1)}{6} $$作为
作为测试，你可以复制上面代码，然后在 https://kmath.cn 的公式里，粘贴进去来查看器效果。
LaTex目前已经成为“数理化”的行业的标准语法。因此，你不用担心学会了在其他系统里无法使用。
在word里，你也可以用LaTex语法写公式。
快速掌握Latex 只要掌握如下几个小技巧，你就能达到高手！！！
（1）Latex的命令都已“”\“开头，每个命令使用 {} 包括，通常 {}后面识别一个字符
例如 \dfrac 表示分数，而分数由分子和分母组成，因此就表示为
$ \dfrac{1}{2} $
表示的是二分之一
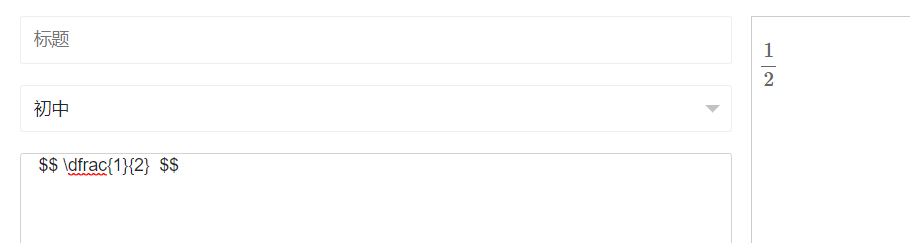
如果你写成 $$ \dfrac127 $$ 可能就不是你想要的，所以多使用{}很有必要
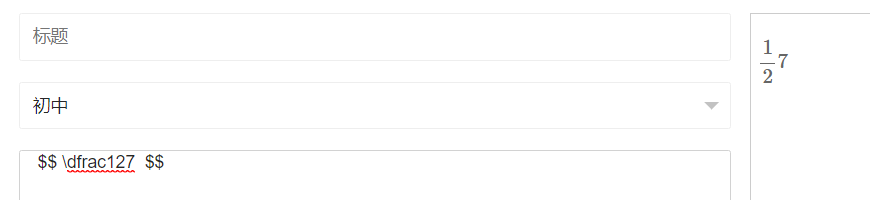
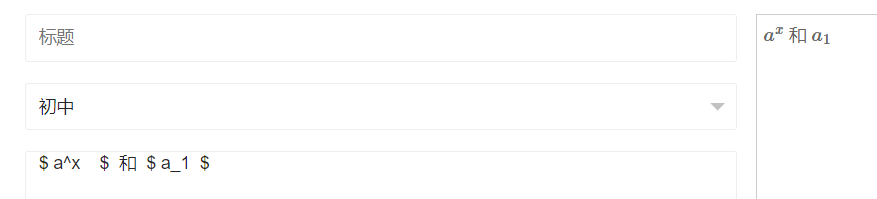
（2） ^ 表示上标，_ 表示下标
(3) \\ 表示换行
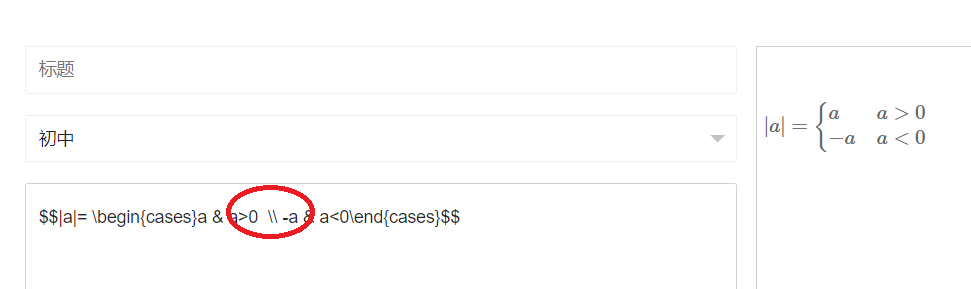
熟悉了上面的小技巧，看下面的公司应该很容了。
如果实在不会了怎么吧？
在线手写啊！
Kmath带另一个在线手写，让系统自动生成Latex
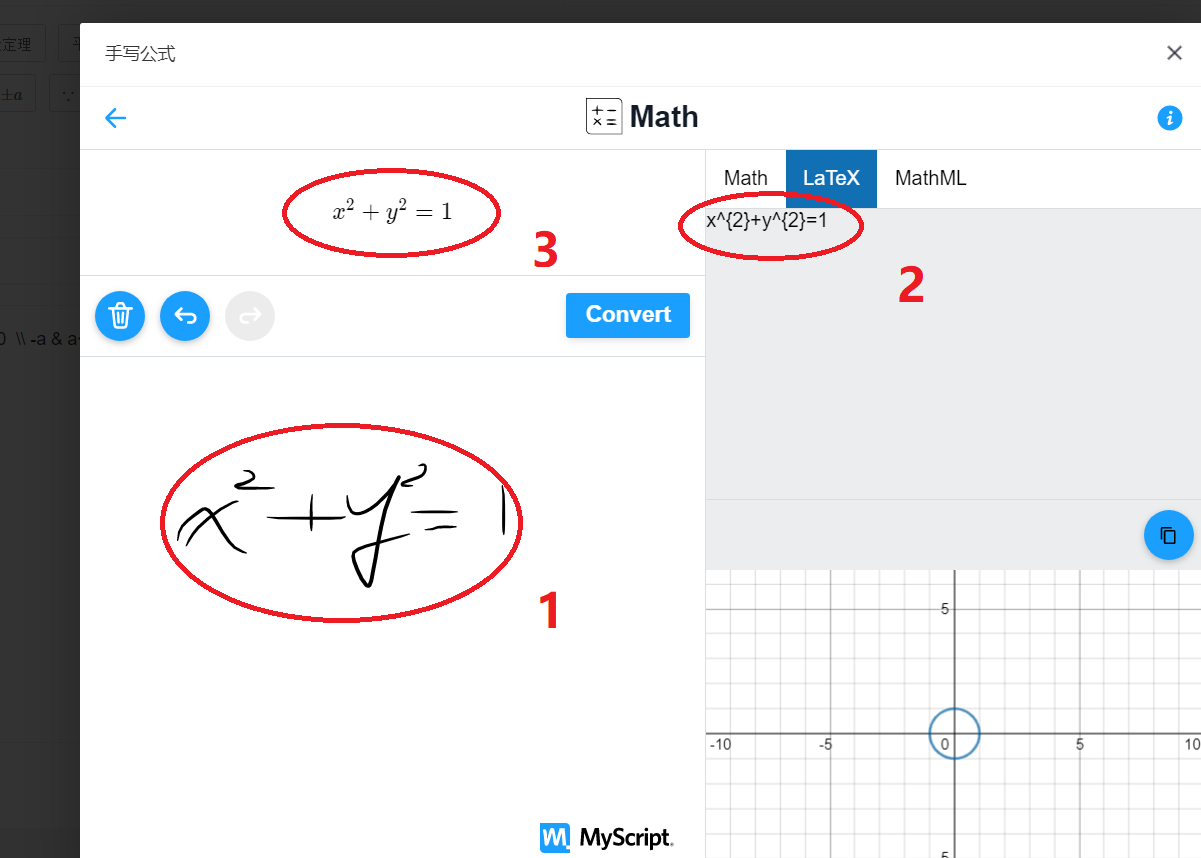
Latex就那么多命令，一旦记住，终身受用。
\frac{\partial u}{\partial t}
= h^2 \left( \frac{\partial^2 u}{\partial x^2}
+ \frac{\partial^2 u}{\partial y^2}
+ \frac{\partial^2 u}{\partial z^2} \right) \
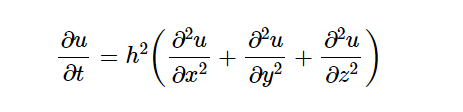
举例2：
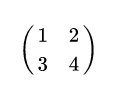
\begin{pmatrix}1&2\\3&4\\ \end{pmatrix}
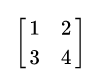
\begin{bmatrix}1&2\\3&4\\ \end{bmatrix}
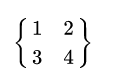
\begin{Bmatrix}1&2\\3&4\\ \end{Bmatrix}
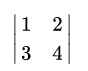
\begin{vmatrix}1&2\\3&4\\ \end{vmatrix}
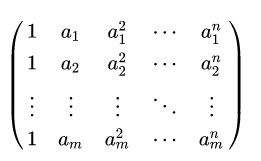
\begin{pmatrix}
1 & a_1 & a_1^2 & \cdots & a_1^n \\
1 & a_2 & a_2^2 & \cdots & a_2^n \\
\vdots & \vdots& \vdots & \ddots & \vdots \\
1 & a_m & a_m^2 & \cdots & a_m^n
\end{pmatrix}
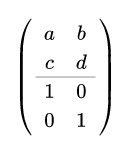
\begin{pmatrix}
a & b\\
c & d\\
\hline
1 & 0\\
0 & 1
\end{pmatrix}
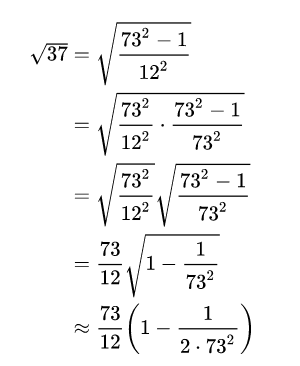
\begin{align}
\sqrt{37} & = \sqrt{\frac{73^2-1}{12^2}} \\
& = \sqrt{\frac{73^2}{12^2}\cdot\frac{73^2-1}{73^2}} \\
& = \sqrt{\frac{73^2}{12^2}}\sqrt{\frac{73^2-1}{73^2}} \\
& = \frac{73}{12}\sqrt{1 - \frac{1}{73^2}} \\
& \approx \frac{73}{12}\left(1 - \frac{1}{2\cdot73^2}\right)
\end{align}
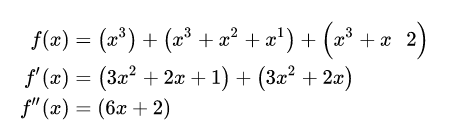
\begin{align} f(x)&=\left(x^3\right)+\left(x^3+x^2+x^1\right)+\left(x^3+x^2\right)\\ f'(x)&=\left(3x^2+2x+1\right)
+
\left(3x^2+2x\right)\\ f''(x)&=\left(6x+2\right)\\ \end{align}
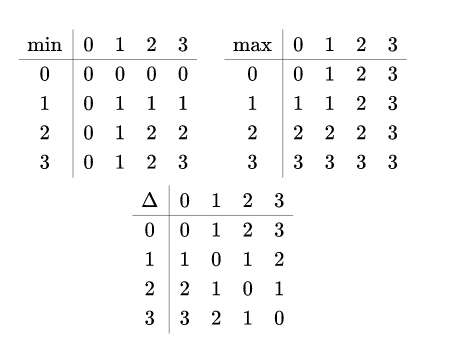
% outer vertical array of arrays
\begin{array}{c}
% inner horizontal array of arrays
\begin{array}{cc}
% inner array of minimum values
\begin{array}{c|cccc}
\text{min} & 0 & 1 & 2 & 3\\
\hline
0 & 0 & 0 & 0 & 0\\
1 & 0 & 1 & 1 & 1\\
2 & 0 & 1 & 2 & 2\\
3 & 0 & 1 & 2 & 3
\end{array}
&
% inner array of maximum values
\begin{array}{c|cccc}
\text{max}&0&1&2&3\\
\hline
0 & 0 & 1 & 2 & 3\\
1 & 1 & 1 & 2 & 3\\
2 & 2 & 2 & 2 & 3\\
3 & 3 & 3 & 3 & 3
\end{array}
\end{array}
\\
% inner array of delta values
\begin{array}{c|cccc}
\Delta&0&1&2&3\\
\hline
0 & 0 & 1 & 2 & 3\\
1 & 1 & 0 & 1 & 2\\
2 & 2 & 1 & 0 & 1\\
3 & 3 & 2 & 1 & 0
\end{array}
\end{array}
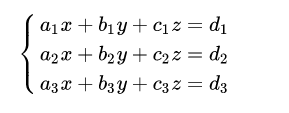
\left\{
\begin{array}{c}
a_1x+b_1y+c_1z=d_1 \\
a_2x+b_2y+c_2z=d_2 \\
a_3x+b_3y+c_3z=d_3
\end{array}
\right.
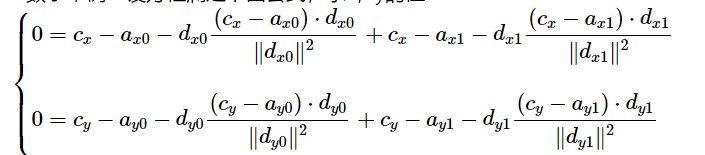
\left\{ \begin{array}{l}
0 = c_x-a_{x0}-d_{x0}\dfrac{(c_x-a_{x0})\cdot d_{x0}}{\|d_{x0}\|^2} + c_x-a_{x1}-d_{x1}\dfrac{(c_x-a_{x1})\cdot d_{x1}}{\|d_{x1}\|^2} \\[2ex]
0 = c_y-a_{y0}-d_{y0}\dfrac{(c_y-a_{y0})\cdot d_{y0}}{\|d_{y0}\|^2} + c_y-a_{y1}-d_{y1}\dfrac{(c_y-a_{y1})\cdot d_{y1}}{\|d_{y1}\|^2} \end{array} \right.
