一个看似简单的查找算法 —— 二分查找算法

前言

二分查找算法应该是非常常见的一个算法了，查找速度快，算法逻辑简单是大家对该算法的一个大致印象。

相信有很多同学能够在很短的时间内写出一个二分查找算法，即便记不太清二分查找算法的逻辑，稍微搜一下，瞟一眼，就能迅速回忆起该算法的大致逻辑，然后迅速写出来该算法。

但是，实际上二分查找算法可不只是那么简单的一个算法，据说第一个二分查找算法与1946年出现，但是第一个完全正确的二分查找算法实现直到1962年才出现。

有很多的边界问题，是不太好处理的。题主这篇文章所阐述的二分查找算法也有可能不是一个完善的算法，但是会尽力把目前我所知道的一些坑给解决掉。

正文

首先，先来看一下二分查找的伪代码：

假设我们有一个有序数组 [1, 2, 3, 5, 5, 5, 6]，我们要在这个数组里面找到给定数字的位置，如果该数字在该数组中存在多个，则返回任意一个就可以。

那么伪代码可以这样写：

func BinarySearch(list []int, target int) int {
        l := 0
        r := len(list) -1
        for l <= r {
            // 如果用 (r+l)/2来计算mid，有可能会因为r+l造成数据范围溢出
            mid := l + ((r - l) >>1)
            if (list[mid] > target) {
                  r = mid - 1
            } else if (list[mid] < target) {
                  l = mid +1
            } else {
                  return mid
            }
         }
        return -1
}        

这种情况下不会出现死循环的情况。

还是刚才的数组 [1, 2, 3, 5, 5, 5, 6]，我们要在这个数组里面找到给定数字的位置，如果存在多个，则需要返回该数字所在的位置中的最后一个。

那么伪代码就不能像刚才那样写了，应该这样写：

func BinarySearch(list []int, target int) int {
        l := 0
        r := len(list) -1
        for l <= r {
            // 如果用 (r+l)/2来计算mid，有可能会因为r+l造成数据范围溢出
            mid := l + ((r - l) >>1)
            if (list[mid] > target) {
                  r = mid - 1
            }
            l = mid
         }
        return l
}    

 假设我们要找的是数字5，下面让我们来推理一下搜索的过程：

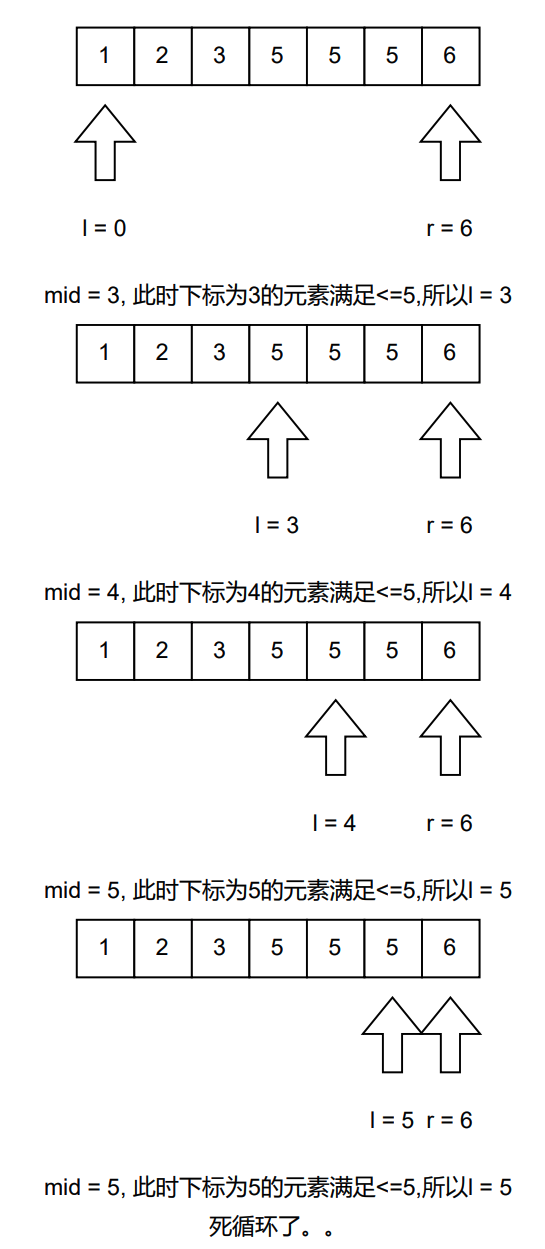
 那么呢，如果我们对计算mid的方法做一些小小的改动，伪代码如下所示：

func BinarySearch(list []int, target int) int {
        l := 0
        r := len(list) -1
        for l <= r {
            // 方便演示，改成这种形式，其实就是向上取整
            mid := (l+r+1) / 2
            if (list[mid] > target) {
                  r = mid - 1
            }
            l = mid
         }
        return l
} 

我们再来看一下整个搜索过程：

 之所以死循环，其实跟我们判断循环终止的条件有很大的关系，那么我们再来改一下代码：

func BinarySearch(list []int, target int) int {
        l := 0
        r := len(list) -1
        for l < r {
            // 方便演示，改成这种形式，其实就是向上取整
            mid := (l+r+1) / 2
            if (list[mid] > target) {
                  r = mid - 1
            }
            l = mid
         }
　　　　 if list[l] = target {
　　　　　　　return l
　　　　 }
        return -1
} 

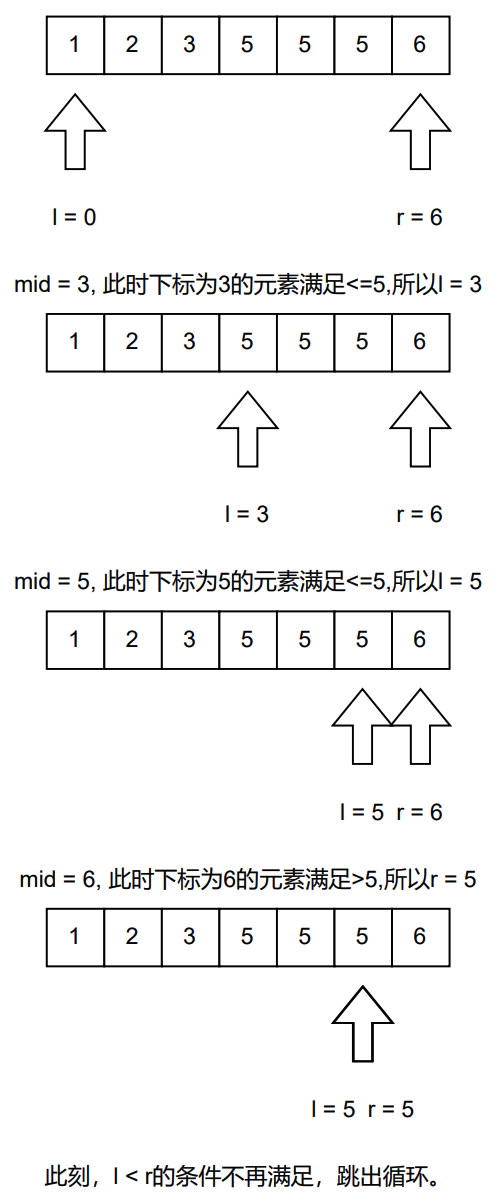
 这下终于不会再死循环了。

总结

1. 常规的二分查找（如果目标元素在有序数组中有多个，可以返回任一位置的那种），这个时候我们写二分查找的写法一般都是三个判断条件，分别是:list[mid] > target; list[mid] < target; list[mid] == target;  这种情况，我们是不会出现死循环的，因为目标数字存在立即就返回了，如果不存在, l <= r 的这个判断条件迟早会不满足。也就是说mid要么是答案所在位置，要么不是，l 和 r 永远不会等于 mid。
2. 非常规的二分查找（如果目标元素在有序数组中有多个，返回第一个或者最后一个目标元素所在的位置），这个时候我们写二分查找的写法一般都是两个判断条件，我们往往会把之前三个判断条件中的 大于 或者 小于中的其中一个判断条件改成 大于等于 或者 小于等于。这种情况，很容易出现死循环。因为mid所在位置也有可能是答案所在的位置点，所以我们往往不会直接跳过mid，我们会在判断后，让 l = mid 或者 r = mid。
   当 l 和 r 是相邻位置元素的时候，mid = ( l + r ) / 2 ，假设我们的判断条件是 if list[mid] >= target ; l = mid; 假设满足了条件，那么我们会发现这个时候l经过计算 会一直停留在 l = ( l + r ) / 2的这个位置上，除非我们能打破这个平衡。
   这个时候我们可以引入向上取整，  mid = ( l + r + 1 ) / 2，但是可以看上面的推导示例，好像也是于事无补。
   想要解决死循环问题还需要对循环的终止条件做一个修改，这样才能杜绝死循环的发生。