不常见的排序算法 - 桶排序、计数排序、基数排序
1. 前言
提到排序,我们最先想到的肯定是常见的那些排序算法:
选择排序、冒泡排序、快速排序、归并排序
考虑到性能的情况下,我们应该会优先使用快速排序,因为它的平均时间复杂度是 O(n*logn),至于归并排序,虽然它也是一个拥有O(n*logn)平均时间复杂的一个算法,但是它的空间复杂度较快排也较为苛刻,它需要O(nlogn)的空间复杂度,而快排在理想情况下,仅需要O(logn)的空间复杂度。
这些常见的排序算法有一个共同点,那就是它们在给一个无序的数组排序的过程中,会对数字进行比较来决定某个数字最终所在的位置。
那么今天介绍的这三个算法,它们也可以完成对一堆无序的数字进行排序,它们无需对数字进行严格的比较,或者说不全是对数字进行比较,也可以使得一个无序的数据序列变为有序的,下面就让我们一起来学习一下这三个算法吧。
2. 算法介绍
2.1 桶排序
桶排序,我们第一时间听到这个名词,会联想到什么,是不是会联想到一个又一个的桶,每个桶里装满了数字,每个桶只能装具有某些特征的数字。
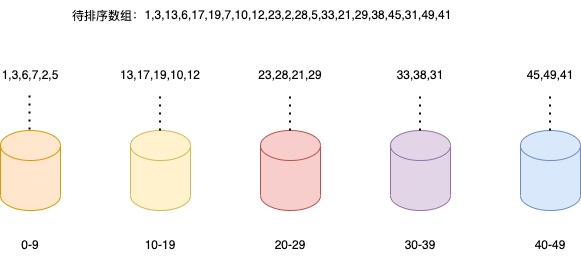
例如上图,我们预定义了五个桶,每个桶只能存放某个数据范围的数字,例如第一个桶只能存放大于等于0且小于等于9的数字,以此类推。
我们对每个桶里的数字运用那些常见的排序算法进行排序,例如:快速排序,用快排对五个桶里的数据分别排好序后,最后将五个桶里的数字合并成一个,这样整个数据就是全局有序的了。
下面我们来分析一下桶排序的时间复杂度:
假设我们待排序的数据长度为n,假设每个桶大致都分得了m个数据,然后我们又q个桶。
那么有: n = m * q
我们对桶里的数据用快排进行排序,每个桶需要耗费:O(m*logm),那么总的时间复杂度就是: O(q*m*logm),其实就是O(n*logm),然后m = n / q,所以当桶的个数接近于n的时候,
那么最终桶排序的时间复杂度就是O(n)了,它的空间复杂度同样也是O(n)。
这里对桶排序做一下总结:
首先能否使用桶排序,它主要取决于待排序的数字是否具有上述特征,即数字分布比较均匀,且数据跨度大,以至于我们可以将数字均匀地分散到各个桶里面去。
其次呢,个人觉得桶排序不适合排序规模较小的数据,因为O(n)和O(nlogn)似乎在数据规模较小的时候,排序所需的时间相差不是很多,空间复杂度O(n)和O(logn)似乎相差也不是很多;而数据规模比较大的时候就不一样了,时间复杂度上相差较大,如果可以用桶排序则优先用桶排序。
而且在空间复杂度上的考量,如果数据量很大,几十GB的那种,用快排似乎一台计算机的内存扛不住。而如果我们用桶排序,那么假设我们分为10000个桶,每个桶里那么差不多有几兆数据,假设计算机是八核的,那么同一时刻也就八个桶在计算机内存中排序,对空间的占用也就是几十兆,对内存毫无压力,这个时候桶排序的优势就体现出来了。
用一般的排序方法需要将所有数据加载到内存里,但是桶排序不用,有效的解决了内存不足的问题,而且如果数据分布较广且规律,效率可以达到O(n),不失为一个很优秀的排序算法了。
伪代码:
由于我比较懒,这个伪代码比较随意。。大致写一下思路
func bucketInsideSort(bucket []int) {
// 桶内排序,可以选择快排
...
}
func splitMultipleBuckets(sourceNum interface) [][]int {
// 对原始数据进行分桶,有可能给的是一个文件路径
// 首先要分多少个桶,每个桶的数据范围是多少
// 然后往每个桶里分数据
}
func mergeAllBuckets(buckets interface) {
// 对所有bucket进行merge,如果是外部文件排序的话,则可以对文件名归纳整理
// 例如:文件1,文件2,文件3,以此存放着从低到高的有序数据
...
}
func main() {
splitMultipleBuckets()
for _, bucket :=range allBuckets {
bucketInsideSort(bucket)
}
mergeAllBuckets
}
2.2 计数排序
有了前面桶排序的经验,再来理解计数排序就不难了,其实可以把计数排序理解为一种特殊的桶排序,可以看以下这张图:
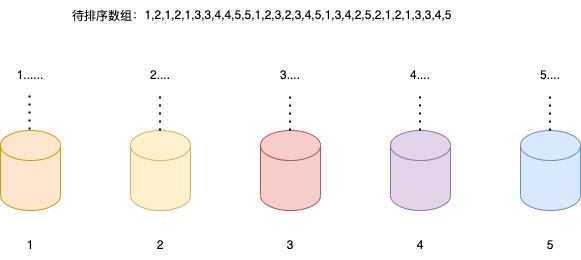
假设待排序的数组长度为n,而且这个数组的数据范围也不大,比如最小值是1,最大值是5,那我们就可以按照这个数据特征来创建5个桶,每个桶里只存放等值数据,例如第一个桶只放1,以此类推。
我们最后只需要记录每个桶里有多少个数据,就可以完成对全局数据的排序,相对于桶排序,连桶内的快排都省了。
你可能会想哪有那么好的事,具有这样数据特征的数据还需要我们排序吗?
其实这样的数据在生活中应该挺常见的,例如对某个全国性的考试分数进行排序,因为分数数据范围是有限的,而考生人数可能是众多的,假如分数范围为0-100,考生人数假设有上千万,那么这个时候,我们只需要分100个桶,即可以轻松的完成对考生成绩的排序。
时间复杂度是O(n),空间复杂度是O(m+n),m代表分的桶的个数,如果数据范围不大的话,对内存的要求还挺低的。
下面提供一下计数排序的伪代码,计算排序的逻辑会稍微复杂一些,所以伪代码也会详细一些。
假设我们有待排序的数组为 nums[]int: 2, 5, 3, 0, 2, 3, 0, 3
那么我们的桶计数的数组为bucket[]int: 2, 0, 2, 3, 0, 1
↓ ↓ ↓ ↓↓↓
其中下标代表桶里装的数字: 0, 1, 2, 3, 4, 5, 所以0有2个,1有0个,2有2个,3有3个,4有0个,5有1个。
那么根据这两个数组nums[]int, bucket[]int,我们要怎么对nums[]int进行排序呢。
你可能会想,最简单的,直接便利bucket[]int不就可以了吗,例如下述代码:
func countSort(nums[]int)[]int{
// 对nums进行分桶统计
// 我们省去计算分桶的个数的步骤
bucketNums := 6
bucket := make([]int,0,6)
for _, num := range nums {
bucket[num] +=1
}
for j:=0; j<len(bucket); j++ {
numsIndex := 0
for i:=0;i<bucketNumber; i++{
// 直接根据bucket里的数值对nums进行填充
nums[numsIndex] = bucket[j]
numsIndex ++
}
}
return nums
}
这样其实也行,但是如果我们对排序算法的要求是稳定排序(即数据相对位置不变),那这样就不行了😅
这里有一个巧妙的处理方法,就是对桶以此相加:
相加前:2, 0, 2, 3, 0, 1
相加后:2, 2, 4, 7, 7, 8, 我们把相加后的数组记为:newBucket[]int,那么这个新数组有什么含义呢?
newBucket[i]代表了小于等于i这个数字的总个数,例如newBucket[3] = 7,那说明小于等于3的数字一共有7个,真实情况确实如此。
小于等于7的数字有:2个0,2个2,3个3,针对这个特征,我们可以从后往前遍历原始数组nums[]int,然后根据newBucket[]int可以算出来某个数字在排好序的数组中的位置,这里我们还需要一个新的数组来放置最终排序好的数组。
下图是我转载自 极客时间 王争老师的《数据结构与算法》课程中的插图,这个图画的太好了,仅供参考。

伪代码:
func countSort(nums[]int) []int{
// 同样假设我们已经知道了桶的个数,这里就是6,省个事。。
bucketSize = 6
bucket :=make([]int,0,6)
for i:=0;i<len(nums);i++{
bucket[nums[i]]++
}
// 上面已经统计好桶了,下一步,累加桶内数据,巧妙的点
for i:=1;i<len(bucket);i++{
bucket[i] = bucket[i] + bucket[i-1]
}
// 累加好了,下一步开始填充数据了,先new一个新数组
res :=make([]int,0,len(nums))
for i:= len(nums)-1;i>=0;i--{
// bucket[nums[i]]代表了当前有多少个数字小于等于nums[i],再减去1,就是实际在res数组中的位置了
res[bucket[nums[i]]-1] = nums[i]
// 因为已经放置了一个nums[i],所以当前小于等于nums[i]也要减1
bucket[nums[i]] -= 1
}
return res
}
注意:这里如果你要从前往后遍历nums[]int,也不是不可以,只是bucket[]int的特性需要我们从后往前遍历,只有这样才能是一个稳定的算法。
2.3 基数排序
基数排序,顾名思义。我们要着重关注“基数”这个词,假设我们有一堆待排序的数据,那么数据的“基数”是什么呢?
首先我们不能说这堆待排序的数据中的任一数据是“基数”,因为待排序中的序列中的任何一个数据就是一个数据,我们可以称之为待排元素,没必要用“基数”这个称谓来给它赋予新意义。
那么“基数”是不是比待排元素还要小的单位呢?很有可能,假设待排元素是手机号,我们有几十亿个手机号需要排序,按照升序排序。
因为手机号是由11个数字位组成的,如果我们对手机号第一个数字至最后一个数字依次按照一个稳定的、复杂度为o(n)的算法来排序的话,那么经过11次稳定排序,手机号就会按照升序排序。
怎么样,听起来是不是很简单,为什么要使用稳定排序呢?
举个例子,假设读小学五年级的小明,有个好朋友小亮,期末考试成绩下来后,小明问小亮考了多少分,小亮也反问小明考了多少分,好家伙,看来两人都不愿意说出自己的分数,却又想知道对方考了多少分。
这个时候小虎走过来说,你们问对方的分数,不就是想知道自己是不是比对方分数高吗?
小明和小亮坏笑的点点头。
小虎说,我有个好方法,首先我先确认你们的分数的位数,如果位数不一致,就没的比了。经过确认,小明和小亮的分数都是两位数。
小虎说,小明你分数的第一位数字是几?
小明忐忑地说,是9.
小亮也不甘示弱,我也是9.
小虎说,好的,那么不用担心,两位成绩考的都不错,大方的说出第二位数字吧,因为你们第一位数字是相等的,所以还有必要往后面比较一轮。
小明坏笑的说,第二位还是9😏
小亮听后瞬间垂头丧气,小虎都开始安慰小亮了。
小亮说,我第二位也是9😏,哈哈哈,没想到吧。
听后三人相视一笑,小虎说,知道我为什么心无波澜吗,小明和小亮恍然,小虎说因为我的分数是三位数的😁
听到这里,你是不是都觉得你会基数排序了。先别着急,这个时候小明和小亮觉得自己考的分数没有小虎高,就决定想试试小虎的水。
于是他们说,既然你这么会排序,那么我再喊来两个同学,你还能用刚才的方法给我们排序吗?
小虎坏笑着说,难不倒我,再喊来20个同学都可以😁。
于是小明和小亮喊来了,小帅和小美。
小虎说,开始吧,首先确认一下你们的分数是几位数字,四人齐声说,都是两位。
小虎点了下头,又说,那么分别报出你们的第一位数字吧。
小明:9,小亮:9,小帅:9,小美:8
小虎记下此时的排序: 小明=小亮=小帅>小美
小虎自信的点了下头,又说,那么分别报出你们的第二位数字吧。
小明:9,小亮:9,小帅:5,小美:9
小虎记下此时的排序:小明=小亮=小美>小帅
小虎胸有成竹的说,最终排序是:小明=小亮=小美>小帅
小美和小帅相视一笑,很尴尬,小虎还在洋洋得意呢。小美便反驳道:我期末考试失误了,考了89,你怎么能说我比小帅95还要高呢?
小虎一听,心想,啊对。排错了,小虎又挠头又转圈的,过了一会,想到了问题所在。第一轮排序小帅是比小美要高的,但是第二轮排序,小美又比小帅高,但是依照高位优先,小帅是大于小美的。
这个方法心里想想就差不多了,但是似乎第二轮排序还需要记录第一轮排序的结果,才可以排的下去,这岂不是太麻烦了。转念一想,如果从低位开始排序呢,尽管小美在低位上比小帅分数高,但是高位上就比不过了啊。
小虎说道,抱歉了,我刚才的方法不对,这次再来。
我们先从第二位开始,再从第一位开始。。。
这下终于对了!
怎么样,这个例子能帮助我们理解吗😂
好了,回归正题,基数排序对要排序的数据是有要求的,需要可以分割出独立的“位”,而且位之间对最终的排序有递进的关系。这个关系呢,就是,如果a数据的高位比b数据的相同位的数字大,那剩下的低位就不用比较了。
然后呢,每一年的数据范围也不能太大,要可以用线性排序算法来排序,否则,基数排序的时间复杂度就无法做到o(n)了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号