TensorFlow2.1入门学习笔记(16)——使用RNN,LSTM,GRU实现股票预测
文章首发:xmoon.info
Embedding
独热码:数量大,过于稀疏,映射之间是独立的,没有表现出关联性
Embedding:一种单词编码方法,以低维向量实现了编码,这种编码通过神经网络训练优化,能表达出单词的相关性。
- TF描述Embedding层
tf.keras.layers.Embedding(词汇表大小,编码维度)
# 编码维度就是用几个数字表达一个单词
# 对1-100进行编码, [4] 编码为 [0.25, 0.1, 0.11]
tf.keras.layers.Embedding(100, 3 )
- 入Embedding时, x_train维度:[送入样本数, 循环核时间展开步数]
RNN使用Embedding 编码,预测下一个字母
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dense, SimpleRNN, Embedding
import matplotlib.pyplot as plt
import os
input_word = "abcdefghijklmnopqrstuvwxyz"
w_to_id = {'a': 0, 'b': 1, 'c': 2, 'd': 3, 'e': 4,
'f': 5, 'g': 6, 'h': 7, 'i': 8, 'j': 9,
'k': 10, 'l': 11, 'm': 12, 'n': 13, 'o': 14,
'p': 15, 'q': 16, 'r': 17, 's': 18, 't': 19,
'u': 20, 'v': 21, 'w': 22, 'x': 23, 'y': 24, 'z': 25} # 单词映射到数值id的词典
training_set_scaled = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 13, 14, 15, 16, 17, 18, 19, 20,
21, 22, 23, 24, 25]
x_train = []
y_train = []
for i in range(4, 26):
x_train.append(training_set_scaled[i - 4:i])
y_train.append(training_set_scaled[i])
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 使x_train符合Embedding输入要求:[送入样本数, 循环核时间展开步数] ,
# 此处整个数据集送入所以送入,送入样本数为len(x_train);输入4个字母出结果,循环核时间展开步数为4。
x_train = np.reshape(x_train, (len(x_train), 4))
y_train = np.array(y_train)
model = tf.keras.Sequential([
Embedding(26, 2),
SimpleRNN(10),
Dense(26, activation='softmax')
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.01),
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=False),
metrics=['sparse_categorical_accuracy'])
checkpoint_save_path = "./checkpoint/rnn_embedding_4pre1.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True,
monitor='loss') # 由于fit没有给出测试集,不计算测试集准确率,根据loss,保存最优模型
history = model.fit(x_train, y_train, batch_size=32, epochs=100, callbacks=[cp_callback])
model.summary()
file = open('./weights.txt', 'w') # 参数提取
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
############################################### show ###############################################
# 显示训练集和验证集的acc和loss曲线
acc = history.history['sparse_categorical_accuracy']
loss = history.history['loss']
plt.subplot(1, 2, 1)
plt.plot(acc, label='Training Accuracy')
plt.title('Training Accuracy')
plt.legend()
plt.subplot(1, 2, 2)
plt.plot(loss, label='Training Loss')
plt.title('Training Loss')
plt.legend()
plt.show()
################# predict ##################
preNum = int(input("input the number of test alphabet:"))
for i in range(preNum):
alphabet1 = input("input test alphabet:")
alphabet = [w_to_id[a] for a in alphabet1]
# 使alphabet符合Embedding输入要求:[送入样本数, 时间展开步数]。
# 此处验证效果送入了1个样本,送入样本数为1;输入4个字母出结果,循环核时间展开步数为4。
alphabet = np.reshape(alphabet, (1, 4))
result = model.predict([alphabet])
pred = tf.argmax(result, axis=1)
pred = int(pred)
tf.print(alphabet1 + '->' + input_word[pred])
- 运行结果
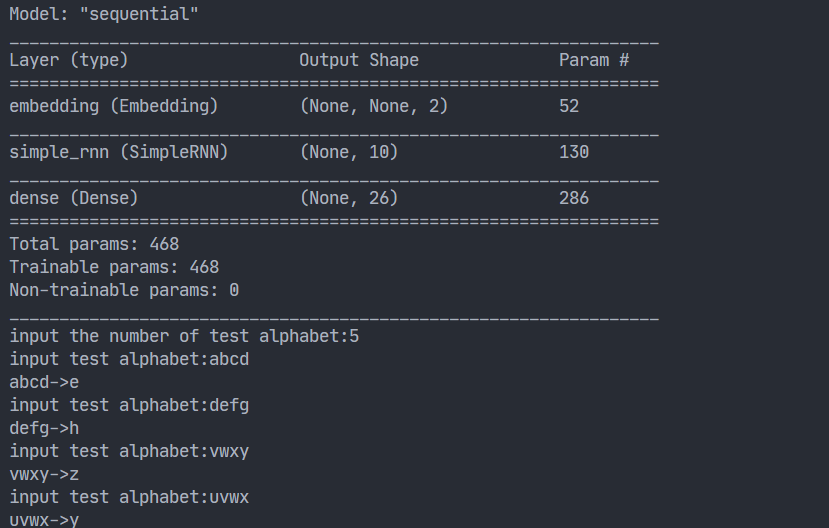
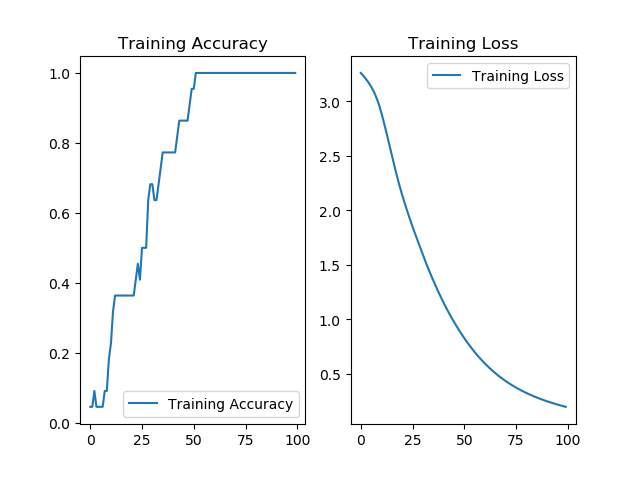
用RNN实现股票预测
- 数据源
使用tushare模块下载股票数据,TuShare是一个著名的免费、开源的python财经数据接口包。其官网主页为:TuShare -财经数据接口包。该接口包如今提供了大量的金融数据,涵盖了股票、基本面、宏观、新闻的等诸多类别数据(具体请自行查看官网),并还在不断更新中。TuShare可以基本满足量化初学者的回测需求
import tushare as ts
import matplotlib.pyplot as plt
df1 = ts.get_k_data('600519', ktype='D', start='2010-06-22', end='2020-06-22')
datapath1 = "./BSH600519.csv"
df1.to_csv(datapath1)
代码
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dropout, Dense, SimpleRNN
import matplotlib.pyplot as plt
import os
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
maotai = pd.read_csv('./BSH600519.csv') # 读取股票文件
training_set = maotai.iloc[0:2426 - 300, 2:3].values # 前(2426-300=2126)天的开盘价作为训练集,表格从0开始计数,2:3 是提取[2:3)列,前闭后开,故提取出C列开盘价
test_set = maotai.iloc[2426 - 300:, 2:3].values # 后300天的开盘价作为测试集
# 归一化
sc = MinMaxScaler(feature_range=(0, 1)) # 定义归一化:归一化到(0,1)之间
training_set_scaled = sc.fit_transform(training_set) # 求得训练集的最大值,最小值这些训练集固有的属性,并在训练集上进行归一化
test_set = sc.transform(test_set) # 利用训练集的属性对测试集进行归一化
x_train = []
y_train = []
x_test = []
y_test = []
# 测试集:csv表格中前2426-300=2126天数据
# 利用for循环,遍历整个训练集,提取训练集中连续60天的开盘价作为输入特征x_train,第61天的数据作为标签,for循环共构建2426-300-60=2066组数据。
for i in range(60, len(training_set_scaled)):
x_train.append(training_set_scaled[i - 60:i, 0])
y_train.append(training_set_scaled[i, 0])
# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 将训练集由list格式变为array格式
x_train, y_train = np.array(x_train), np.array(y_train)
# 使x_train符合RNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。
# 此处整个数据集送入,送入样本数为x_train.shape[0]即2066组数据;输入60个开盘价,预测出第61天的开盘价,循环核时间展开步数为60; 每个时间步送入的特征是某一天的开盘价,只有1个数据,故每个时间步输入特征个数为1
x_train = np.reshape(x_train, (x_train.shape[0], 60, 1))
# 测试集:csv表格中后300天数据
# 利用for循环,遍历整个测试集,提取测试集中连续60天的开盘价作为输入特征x_train,第61天的数据作为标签,for循环共构建300-60=240组数据。
for i in range(60, len(test_set)):
x_test.append(test_set[i - 60:i, 0])
y_test.append(test_set[i, 0])
# 测试集变array并reshape为符合RNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]
x_test, y_test = np.array(x_test), np.array(y_test)
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))
model = tf.keras.Sequential([
SimpleRNN(80, return_sequences=True),
Dropout(0.2),
SimpleRNN(100),
Dropout(0.2),
Dense(1)
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='mean_squared_error') # 损失函数用均方误差
# 该应用只观测loss数值,不观测准确率,所以删去metrics选项,一会在每个epoch迭代显示时只显示loss值
checkpoint_save_path = "./checkpoint/rnn_stock.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True,
monitor='val_loss')
history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), validation_freq=1,
callbacks=[cp_callback])
model.summary()
file = open('./weights.txt', 'w') # 参数提取
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
################## predict ######################
# 测试集输入模型进行预测
predicted_stock_price = model.predict(x_test)
# 对预测数据还原---从(0,1)反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原---从(0,1)反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='MaoTai Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted MaoTai Stock Price')
plt.title('MaoTai Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('MaoTai Stock Price')
plt.legend()
plt.show()
##########evaluate##############
# calculate MSE 均方误差 ---> E[(预测值-真实值)^2] (预测值减真实值求平方后求均值)
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差--->sqrt[MSE] (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差----->E[|预测值-真实值|](预测值减真实值求绝对值后求均值)
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print('均方误差: %.6f' % mse)
print('均方根误差: %.6f' % rmse)
print('平均绝对误差: %.6f' % mae)
训练结果
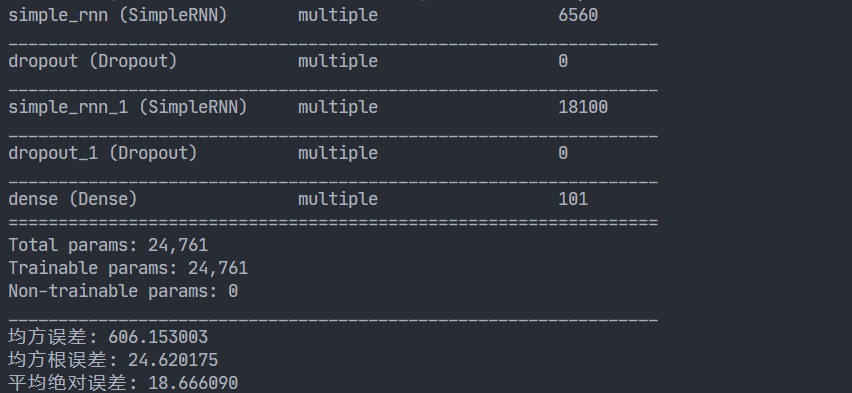
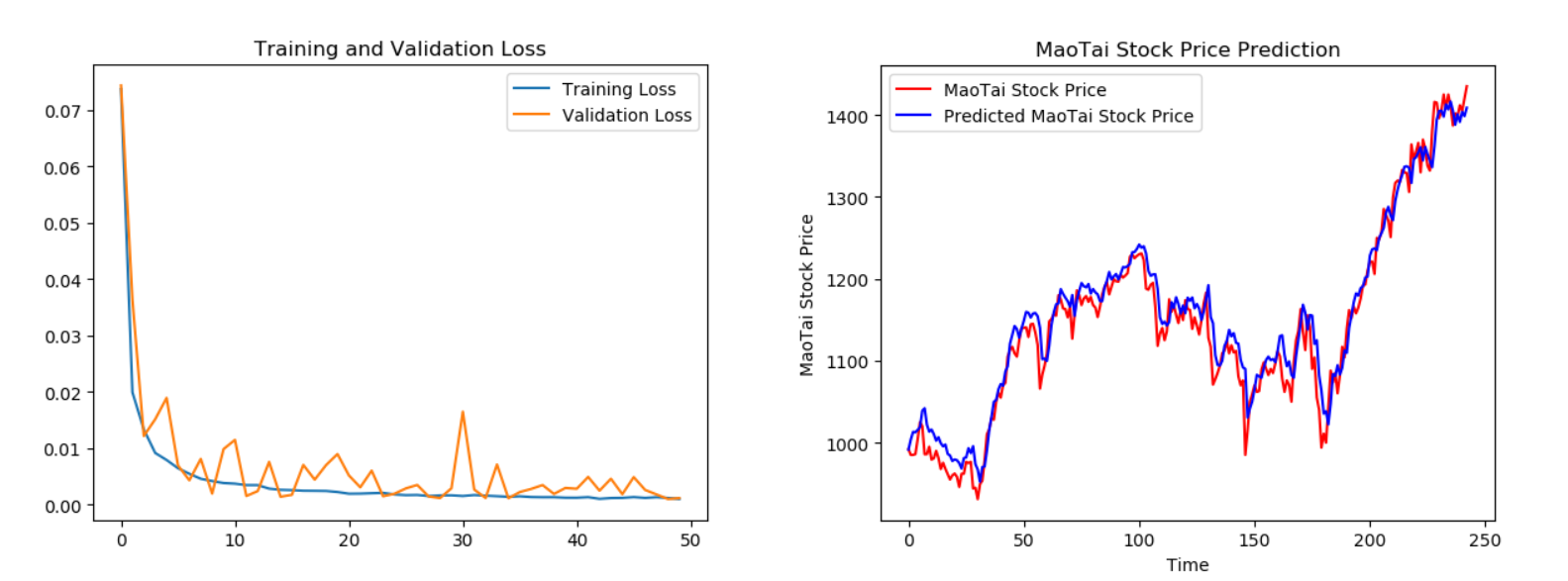
用LSTM实现股票预测
传统的RNN网络可以通过记忆体实现短期记忆,进行连续数据的预测,但是当连续数据过长时,会使展开的时间步过长,在反向传播更新参数时,梯度要按时间步连续相乘会导致梯度消失。
-
LSTM 由Hochreiter & Schmidhuber 于1997年提出,通过门控单元改善了RNN长期依赖问题。
Sepp Hochreiter,Jurgen Schmidhuber.LONG SHORT-TERM MEMORY.Neural Computation,December 1997 -
LSTM计算过程
输入门:\(i_t = \sigma (W_i) \cdot [h_{t-1},x_t] + b_i\)
遗忘门:\(f_t = \sigma (W_f) \cdot [h_{t-1},x_t] + b_f\)
输出门:\(o_t = \sigma (W_o) \cdot [h_{t-1},x_t] + b_o\)
细胞态(长期记忆):\(C_t = f_t \cdot C_{t-1} + i_t\cdot \breve{C_t}\)
记忆体(短期记忆):\(h_t = o_t \cdot tanh(C_t)\)
候选体(归纳出的新知识):\(\breve{C_t} = tanh(W_c \cdot [h_{t-1}, x_t] + b_c)\)
-
TF描述LSTM层
tf.keras.layers.LSTM(记忆体个数,return_sequences=是否返回输出)
# 参数
return_sequences=True 各时间步输出ht
return_sequences=False 仅最后时间步输出ht(默认)
# 例
model = tf.keras.Sequential([
LSTM(80, return_sequences=True),
Dropout(0.2),
LSTM(100),
Dropout(0.2),
Dense(1)
])
代码
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dropout, Dense, LSTM
import matplotlib.pyplot as plt
import os
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
maotai = pd.read_csv('./BSH600519.csv') # 读取股票文件
training_set = maotai.iloc[0:2426 - 300, 2:3].values # 前(2426-300=2126)天的开盘价作为训练集,表格从0开始计数,2:3 是提取[2:3)列,前闭后开,故提取出C列开盘价
test_set = maotai.iloc[2426 - 300:, 2:3].values # 后300天的开盘价作为测试集
# 归一化
sc = MinMaxScaler(feature_range=(0, 1)) # 定义归一化:归一化到(0,1)之间
training_set_scaled = sc.fit_transform(training_set) # 求得训练集的最大值,最小值这些训练集固有的属性,并在训练集上进行归一化
test_set = sc.transform(test_set) # 利用训练集的属性对测试集进行归一化
x_train = []
y_train = []
x_test = []
y_test = []
# 测试集:csv表格中前2426-300=2126天数据
# 利用for循环,遍历整个训练集,提取训练集中连续60天的开盘价作为输入特征x_train,第61天的数据作为标签,for循环共构建2426-300-60=2066组数据。
for i in range(60, len(training_set_scaled)):
x_train.append(training_set_scaled[i - 60:i, 0])
y_train.append(training_set_scaled[i, 0])
# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 将训练集由list格式变为array格式
x_train, y_train = np.array(x_train), np.array(y_train)
# 使x_train符合RNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。
# 此处整个数据集送入,送入样本数为x_train.shape[0]即2066组数据;输入60个开盘价,预测出第61天的开盘价,循环核时间展开步数为60; 每个时间步送入的特征是某一天的开盘价,只有1个数据,故每个时间步输入特征个数为1
x_train = np.reshape(x_train, (x_train.shape[0], 60, 1))
# 测试集:csv表格中后300天数据
# 利用for循环,遍历整个测试集,提取测试集中连续60天的开盘价作为输入特征x_train,第61天的数据作为标签,for循环共构建300-60=240组数据。
for i in range(60, len(test_set)):
x_test.append(test_set[i - 60:i, 0])
y_test.append(test_set[i, 0])
# 测试集变array并reshape为符合RNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]
x_test, y_test = np.array(x_test), np.array(y_test)
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))
model = tf.keras.Sequential([
LSTM(80, return_sequences=True),
Dropout(0.2),
LSTM(100),
Dropout(0.2),
Dense(1)
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='mean_squared_error') # 损失函数用均方误差
# 该应用只观测loss数值,不观测准确率,所以删去metrics选项,一会在每个epoch迭代显示时只显示loss值
checkpoint_save_path = "./checkpoint/LSTM_stock.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True,
monitor='val_loss')
history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), validation_freq=1,
callbacks=[cp_callback])
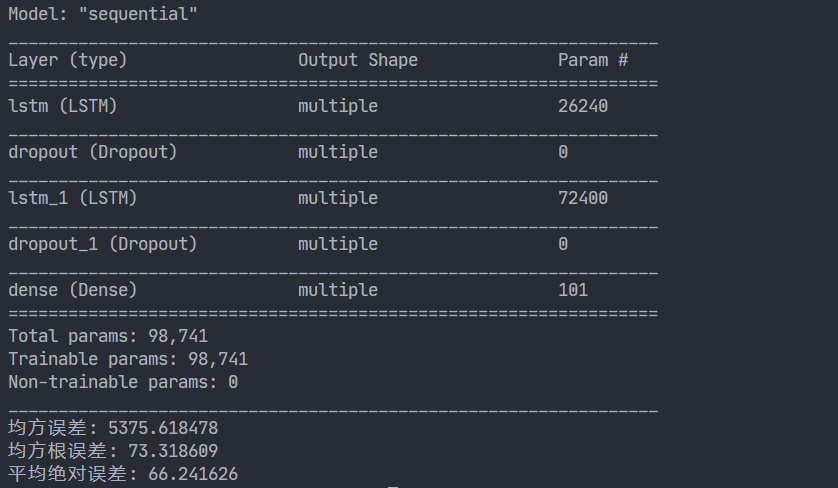
model.summary()
file = open('./weights.txt', 'w') # 参数提取
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
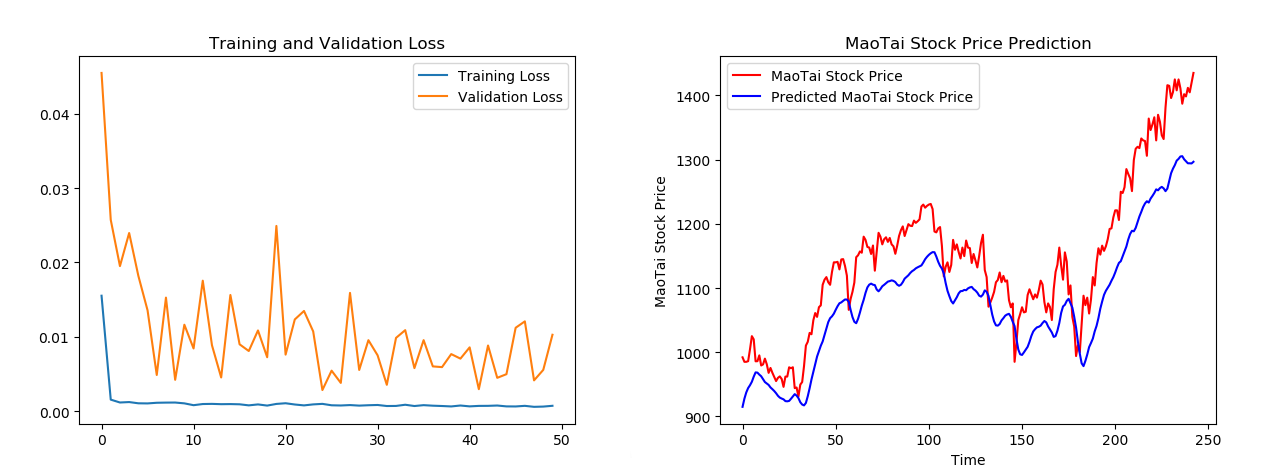
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
################## predict ######################
# 测试集输入模型进行预测
predicted_stock_price = model.predict(x_test)
# 对预测数据还原---从(0,1)反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原---从(0,1)反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='MaoTai Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted MaoTai Stock Price')
plt.title('MaoTai Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('MaoTai Stock Price')
plt.legend()
plt.show()
##########evaluate##############
# calculate MSE 均方误差 ---> E[(预测值-真实值)^2] (预测值减真实值求平方后求均值)
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差--->sqrt[MSE] (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差----->E[|预测值-真实值|](预测值减真实值求绝对值后求均值)
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print('均方误差: %.6f' % mse)
print('均方根误差: %.6f' % rmse)
print('平均绝对误差: %.6f' % mae)
训练结果
用GRU实现股票预测
GRU是由LSTM简化得到的
-
GRU由Cho等人于2014年提出,优化LSTM结构。
Kyunghyun Cho,Bart van Merrienboer,Caglar Gulcehre,Dzmitry Bahdanau,Fethi Bougares,HolgerSchwenk,Yoshua Bengio.Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation.Computer ence, 2014. -
GRU计算过程:
更新门:\(z_t = \sigma(W_z \cdot [h_{t-1}, x_t])\)
重置门:\(r_t = \sigma(W_r \cdot [h_{t-1}, x_t])\)
记忆体:\(h_t = (1-z)\cdot h_{t-1} + z_t \cdot \breve{h_t}\)
候选隐藏层:\(\breve{h_t} = tanh(W \cdot [r_t \cdot h_{t-1}, x_t])\)
-
TF描述GRU层
tf.keras.layers.GRU(记忆体个数,return_sequences=是否返回输出)
# 参数
return_sequences=True 各时间步输出ht
return_sequences=False 仅最后时间步输出ht(默认)
# 例
model = tf.keras.Sequential([
GRU(80, return_sequences=True),
Dropout(0.2),
GRU(100),
Dropout(0.2),
Dense(1)
])
代码
import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Dropout, Dense, GRU
import matplotlib.pyplot as plt
import os
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
maotai = pd.read_csv('./BSH600519.csv') # 读取股票文件
training_set = maotai.iloc[0:2426 - 300, 2:3].values # 前(2426-300=2126)天的开盘价作为训练集,表格从0开始计数,2:3 是提取[2:3)列,前闭后开,故提取出C列开盘价
test_set = maotai.iloc[2426 - 300:, 2:3].values # 后300天的开盘价作为测试集
# 归一化
sc = MinMaxScaler(feature_range=(0, 1)) # 定义归一化:归一化到(0,1)之间
training_set_scaled = sc.fit_transform(training_set) # 求得训练集的最大值,最小值这些训练集固有的属性,并在训练集上进行归一化
test_set = sc.transform(test_set) # 利用训练集的属性对测试集进行归一化
x_train = []
y_train = []
x_test = []
y_test = []
# 测试集:csv表格中前2426-300=2126天数据
# 利用for循环,遍历整个训练集,提取训练集中连续60天的开盘价作为输入特征x_train,第61天的数据作为标签,for循环共构建2426-300-60=2066组数据。
for i in range(60, len(training_set_scaled)):
x_train.append(training_set_scaled[i - 60:i, 0])
y_train.append(training_set_scaled[i, 0])
# 对训练集进行打乱
np.random.seed(7)
np.random.shuffle(x_train)
np.random.seed(7)
np.random.shuffle(y_train)
tf.random.set_seed(7)
# 将训练集由list格式变为array格式
x_train, y_train = np.array(x_train), np.array(y_train)
# 使x_train符合RNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]。
# 此处整个数据集送入,送入样本数为x_train.shape[0]即2066组数据;输入60个开盘价,预测出第61天的开盘价,循环核时间展开步数为60; 每个时间步送入的特征是某一天的开盘价,只有1个数据,故每个时间步输入特征个数为1
x_train = np.reshape(x_train, (x_train.shape[0], 60, 1))
# 测试集:csv表格中后300天数据
# 利用for循环,遍历整个测试集,提取测试集中连续60天的开盘价作为输入特征x_train,第61天的数据作为标签,for循环共构建300-60=240组数据。
for i in range(60, len(test_set)):
x_test.append(test_set[i - 60:i, 0])
y_test.append(test_set[i, 0])
# 测试集变array并reshape为符合RNN输入要求:[送入样本数, 循环核时间展开步数, 每个时间步输入特征个数]
x_test, y_test = np.array(x_test), np.array(y_test)
x_test = np.reshape(x_test, (x_test.shape[0], 60, 1))
model = tf.keras.Sequential([
GRU(80, return_sequences=True),
Dropout(0.2),
GRU(100),
Dropout(0.2),
Dense(1)
])
model.compile(optimizer=tf.keras.optimizers.Adam(0.001),
loss='mean_squared_error') # 损失函数用均方误差
# 该应用只观测loss数值,不观测准确率,所以删去metrics选项,一会在每个epoch迭代显示时只显示loss值
checkpoint_save_path = "./checkpoint/stock.ckpt"
if os.path.exists(checkpoint_save_path + '.index'):
print('-------------load the model-----------------')
model.load_weights(checkpoint_save_path)
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_save_path,
save_weights_only=True,
save_best_only=True,
monitor='val_loss')
history = model.fit(x_train, y_train, batch_size=64, epochs=50, validation_data=(x_test, y_test), validation_freq=1,
callbacks=[cp_callback])
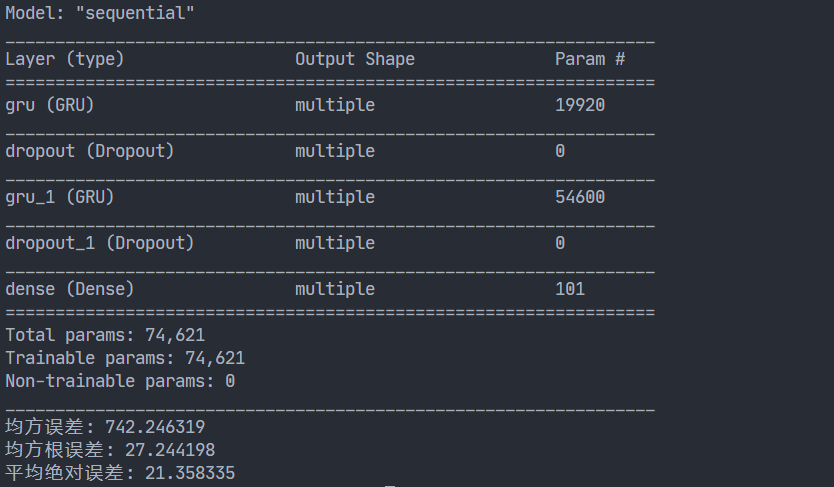
model.summary()
file = open('./weights.txt', 'w') # 参数提取
for v in model.trainable_variables:
file.write(str(v.name) + '\n')
file.write(str(v.shape) + '\n')
file.write(str(v.numpy()) + '\n')
file.close()
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
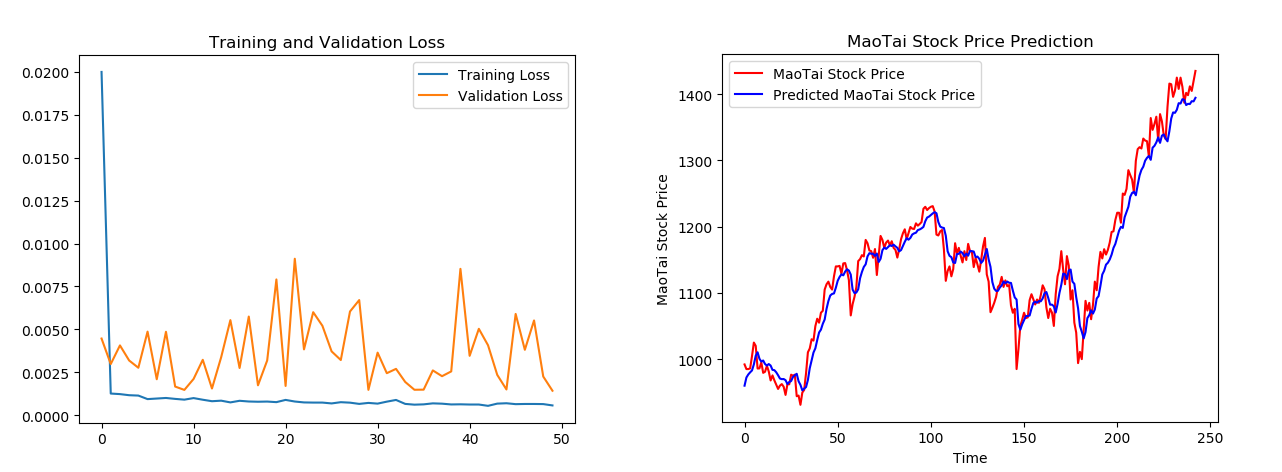
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
################## predict ######################
# 测试集输入模型进行预测
predicted_stock_price = model.predict(x_test)
# 对预测数据还原---从(0,1)反归一化到原始范围
predicted_stock_price = sc.inverse_transform(predicted_stock_price)
# 对真实数据还原---从(0,1)反归一化到原始范围
real_stock_price = sc.inverse_transform(test_set[60:])
# 画出真实数据和预测数据的对比曲线
plt.plot(real_stock_price, color='red', label='MaoTai Stock Price')
plt.plot(predicted_stock_price, color='blue', label='Predicted MaoTai Stock Price')
plt.title('MaoTai Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('MaoTai Stock Price')
plt.legend()
plt.show()
##########evaluate##############
# calculate MSE 均方误差 ---> E[(预测值-真实值)^2] (预测值减真实值求平方后求均值)
mse = mean_squared_error(predicted_stock_price, real_stock_price)
# calculate RMSE 均方根误差--->sqrt[MSE] (对均方误差开方)
rmse = math.sqrt(mean_squared_error(predicted_stock_price, real_stock_price))
# calculate MAE 平均绝对误差----->E[|预测值-真实值|](预测值减真实值求绝对值后求均值)
mae = mean_absolute_error(predicted_stock_price, real_stock_price)
print('均方误差: %.6f' % mse)
print('均方根误差: %.6f' % rmse)
print('平均绝对误差: %.6f' % mae)
训练结果


 浙公网安备 33010602011771号
浙公网安备 33010602011771号