MORL | Envelope Q-Learning：有收敛性保证的 MORL 算法

• 论文标题：A Generalized Algorithm for Multi-Objective Reinforcement Learning and Policy Adaptatio。
• NeurIPS 2019。也许是第一个有收敛性保证的 MORL 算法，理论框架非常优雅。
• arxiv：https://arxiv.org/abs/1908.08342
• pdf：https://arxiv.org/pdf/1908.08342
• html：https://ar5iv.labs.arxiv.org/html/1908.08342
• GitHub：https://github.com/RunzheYang/MORL
• 可以参考的实现：MORL-baseline 里的 EQL 。

---

目录

• 1 多目标强化学习（Multi-Objective Reinforcement Learning, MORL）
  • 1.1 setting
  • 1.2 先前方法的问题
• 2 Preliminaries: Multi-Objective MDP
  • 2.1 Multi-Objective MDP（MOMDP）
  • 2.2 向量 reward \(\boldsymbol r\) 和 weight \(\boldsymbol \omega\) 下的策略与值函数
  • 2.3 求解目标：帕累托前沿
• 3 Method: Envelope Q-Learning
  • • 3.1 Q function 以及 Q 空间中的距离度量
    • 3.2 单目标 bellman 算子的多目标拓展
    • 3.3 理论保证（收敛性）
    • 3.4 具体的 loss function
• 4 tricks
• 5 实验
  • 5.1 task
  • 5.2 baselines
  • 5.3 metrics
  • 5.4 具体实验结果
  • 5.5 细节实验设置
• 6 总结

---

1 多目标强化学习（Multi-Objective Reinforcement Learning, MORL）

1.1 setting

在多目标强化学习中，我们需要同时优化多个竞争目标，如速度、准确率、成本等。这篇文章的 intro 里举了一个例子：一个虚拟助手，与人类沟通以执行特定任务时，根据用户在成功率或简洁性等方面的相对偏好，可能需要遵循完全不同的策略。例如，提供天气报告时，agent 应该提供尽可能正确、详细的回应；在提供一个完成任务的逐轮引导时，agent 需要找到完成任务的最短路径，而非跟用户输出冗长的语言；这个例子说明，研究 MORL agent 在现实世界中是有对应场景的。

我们的目标是学习一个单一模型，能在所有可能的用户偏好下输出最优策略，并支持快速适应 / 自动推断未知的用户偏好。

1.2 先前方法的问题

• 单策略方法：使用一个 weight \(\boldsymbol \omega\) 来代表人类当前的偏好，去跟多目标 reward 做内积，将多目标加权变成单目标 \(r = \boldsymbol\omega^T \boldsymbol r\)；但这种方法只能学一个固定偏好 \(\boldsymbol\omega\)，无法适应未知偏好。
• 多策略方法：对多个 weight \(\omega\) 分别训练独立策略，然后把这些策略都存下来，作为 Pareto 前沿。缺点是成本高，比如当 reward 维度 m > 3 时，难以学大量策略来遍历整个 weight 空间。
• 现有的 deep MORL 方法：如标量化 Q 学习，它们更新时只用一个 \(\omega\)，无法复用其他 \(\omega\) 探索到的最优轨迹，样本效率低。

本文的动机，是去 fill 现有方法的 gap：既要灵活性（适应任意 \(\omega\)），又要可扩展性（不存一堆策略），还要样本效率（一次探索供所有 \(\omega\) 下的策略更新复用）。

关键是让不同 \(\omega\) 下的学习过程能互相促进而非孤立，而 EQL 通过将经典 RL 的 bellman 更新扩展到向量 reward，并定义凸包更新运算符，巧妙地做到了这一点。

2 Preliminaries: Multi-Objective MDP

2.1 Multi-Objective MDP（MOMDP）

一个 MOMDP 可以表示为一个元组：

\[\langle \mathcal{S}, \mathcal{A}, \mathcal{P}, \boldsymbol{r}, \gamma, \Omega, f_{\omega} \rangle \]

其中：

1. \(\mathcal{S}\): 状态空间。

2. \(\mathcal{A}\): 动作空间。

3. \(\mathcal{P}(s' | s, a)\): 状态转移概率分布，表示在状态 \(s\) 执行动作 \(a\) 后转移到状态 \(s'\) 的概率。

4. \(\boldsymbol{r}(s, a)\): 向量奖励函数。这是与标准 MDP 最核心的区别。MOMDP 的 reward 是一个 \(m\) 维向量，其中 \(m\) 是目标的数量：

   \[\boldsymbol{r}(s, a) = [r_1(s, a), r_2(s, a), \dots, r_m(s, a)]^\intercal \in \mathbb{R}^m \]

   每个分量 \(r_i(s, a)\) 代表在状态 \(s\) 执行动作 \(a\) 后，在第 \(i\) 个目标上获得的即时奖励。

5. \(\gamma\): 折扣因子，\(\gamma \in [0, 1)\)，用于计算累积回报。

6. \(\Omega\): weight 空间，或者称为偏好空间。其中的每个元素 \(\boldsymbol{\omega}\) 是一个 \(m\) 维向量，表示决策者对各个目标的相对重要性权衡。

   \[\boldsymbol{\omega} = [\omega_1, \omega_2, \dots, \omega_m]^\intercal \in \Omega \]

   通常，偏好向量被约束在一个 m-1 维的单纯形上，即 \(\sum_{i=1}^m \omega_i = 1\) 且 \(\omega_i \geq 0\)，但这并非绝对要求。

7. \(f_{\omega}(\cdot)\): 偏好函数。它将向量奖励（或回报）根据 weight \(\boldsymbol{\omega}\) 进行加权，转化为一个标量的 utility。在本文关注的线性设置下，其形式为：

   \[f_{\omega}(\boldsymbol{r}(s, a)) = \boldsymbol{\omega}^\intercal \boldsymbol{r}(s, a) = \sum_{i=1}^m \omega_i r_i(s, a) \]

2.2 向量 reward \(\boldsymbol r\) 和 weight \(\boldsymbol \omega\) 下的策略与值函数

我们用策略 \(\pi(a | s, \boldsymbol\omega)\) 表示在 weight \(\boldsymbol \omega\) 下，状态 \(s\) 下选择动作 \(a\) 的概率分布。

1. 向量 return：策略 \(\pi\) 从状态 \(s\) 开始获得的 expected discounted return \(\hat{\boldsymbol{r}}^\pi\)，是一个 \(m\) 维向量：

   \[\hat{\boldsymbol{r}}^\pi(s) = \mathbb{E}_{\pi, \mathcal{P}} \left[ \sum_{t=0}^{\infty} \gamma^t \boldsymbol{r}(s_t, a_t) \ \middle|\ s_0 = s \right] \in \mathbb{R}^m \]

   \(\boldsymbol{v}^\pi(s) = \hat{\boldsymbol{r}}^\pi(s)\) 被称为向量值函数。

2. 标量化的 utility：在给定 weight \(\boldsymbol{\omega}\) 下，策略 \(\pi\) 的标量化 utility 就是其向量 return 跟 weight \(\boldsymbol{\omega}\) 的内积：

   \[U^\pi(s, \boldsymbol{\omega}) = \boldsymbol{\omega}^\intercal \boldsymbol{v}^\pi(s) = \mathbb{E}_{\pi, \mathcal{P}} \left[ \sum_{t=0}^{\infty} \gamma^t \boldsymbol{\omega}^\intercal \boldsymbol{r}(s_t, a_t) \ \middle|\ s_0 = s \right] \]

   这相当于将原始的 MOMDP 转换为一个奖励函数为标量 \(r_\omega(s, a) = \boldsymbol{\omega}^\intercal \boldsymbol{r}(s, a)\) 的标准 MDP。

2.3 求解目标：帕累托前沿

在单目标 RL 中，最优策略是使标量回报最大化的策略。然而，在 MORL 中，目标是冲突的，所有通常不存在一个在所有目标上都最优的“全能”策略。因此，我们引入以下概念：

帕累托最优：一个策略 \(\pi\) 是帕累托最优的，当

1. 不存在另一个策略 \(\pi'\)，使得在所有目标 \(i\) 上都有 \(v_i^{\pi'}(s) \geq v_i^{\pi}(s)\)，即，不存在其他策略 dominate 它；
2. 并且，至少存在一个策略 \(v_j^{\pi}(s)\)，在一个目标 \(j\) 上，\(v^{\pi}(s)\) 严格大于 \(v_j^{\pi}(s)\)。

所有帕累托最优策略对应的向量 return 集合，构成了帕累托前沿 \(\mathcal{F}^*\)。

对于本文关注的 线性偏好 形式，我们关心帕累托前沿的 凸覆盖集（CCS），它是帕累托前沿的凸子集：

\[\texttt{CCS} := \left\{ \hat{\boldsymbol{r}} \in \mathcal{F}^* \ \middle|\ \exists \boldsymbol{\omega} \in \Omega \; \text{ s.t. } \boldsymbol{\omega}^\intercal \hat{\boldsymbol{r}} \geq \boldsymbol{\omega}^\intercal \hat{\boldsymbol{r}}' , \ \forall \hat{\boldsymbol{r}}' \in \mathcal{F}^* \right\} \]

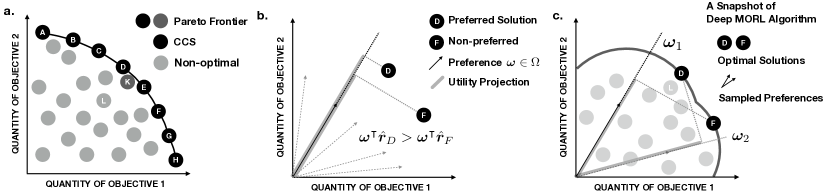
我们解释一下 CCS。如下图 最右的子图所示，帕累托前沿可能是凹的。使用本文的线性 weight 加权多目标方法，没法得到这个 凹 帕累托前沿的全部。具体的，对于前沿上最凹的那个点，因为点 D 和点 F 的向量 return 与凹点的 weight \(w\) 点乘，值反而比凹点的 return 点乘更大，所以 \(w\) 下我们求解的策略，跟点 D / F 处的策略是一样的，而 D F 之间的那一段帕累托前沿，我们求解不到。

3 Method: Envelope Q-Learning

3.1 Q function 以及 Q 空间中的距离度量

首先，论文重新定义了向量 Q function 和衡量两个 Q function 距离的方式。

多目标 Q function：传统的 Q 函数是标量的，而这里定义的是一个向量 Q 函数 \(\boldsymbol{Q}(s, a, \boldsymbol{\omega})\)，它输出一个 \(m\) 维向量，估计在状态 \(s\)、动作 \(a\) 和偏好 \(\boldsymbol{\omega}\) 下的期望向量 discounted return。

\[\boldsymbol{Q}: \mathcal{S} \times \mathcal{A} \times \Omega \rightarrow \mathbb{R}^m \]

整个 Q 空间记为 \(\mathcal{Q} \subseteq (\Omega \rightarrow \mathbb{R}^m)^{\mathcal{S} \times \mathcal{A}}\)。

向量 Q 函数空间中的距离度量：为了在这个空间中进行收敛性分析，我们定义一个伪度量（pseudo-metric），它度量两个向量 Q function 之间的一个标量距离：

\[d(\boldsymbol{Q}, \boldsymbol{Q}') := \sup_{s \in \mathcal{S}, a \in \mathcal{A}, \boldsymbol{\omega} \in \Omega} | \boldsymbol{\omega}^\intercal (\boldsymbol{Q}(s, a, \boldsymbol{\omega}) - \boldsymbol{Q}'(s, a, \boldsymbol{\omega})) | \]

解释：这个度量的值，是两个多目标 Q 函数在 所有状态、动作和 weight 下，其标量化 utility 的最大差异。

它是一个伪度量，因为即使 \(d(\boldsymbol{Q}, \boldsymbol{Q}') = 0\)，\(\boldsymbol{Q}\) 和 \(\boldsymbol{Q}'\) 的向量值也可能在非最优的凹陷处不同，但只要它们对所有 \(\boldsymbol{\omega}\) 的 utility 相同，就被认为是“等价”的。

在接下来，我们将会把 bellman 算子拓展到多目标上，让拓展后的 bellman 算子，对于这个距离定义，是一个压缩映射。

3.2 单目标 bellman 算子的多目标拓展

这是方法的核心，它扩展了经典的单目标 bellman 最优性算子。

首先，我们介绍 Envelope Optimality Filter \(\mathcal{H}\)，这是与传统单目标 Q learning 最根本的区别。标量化方法只对动作 a 取最大值，而我们的的 envelope 方法，同时对动作 a 和 weight w 取最大值。

\[(\mathcal{H}\boldsymbol{Q})(s, \boldsymbol{\omega}) := \arg_{Q} \sup_{a' \in \mathcal{A}, \boldsymbol{\omega}' \in \Omega} \boldsymbol{\omega}^\intercal \boldsymbol{Q}(s, a', \boldsymbol{\omega}') \]

公式解释：

• H 是一个施加于 Q 的 operator，它得到一个 arg Q，这个 Q 是 m 维向量，满足以下条件：它是给定 weight \(\boldsymbol{\omega}\) 下，在下一个状态 \(s'\)，与 \(\boldsymbol{\omega}\) 相乘的 utility 最大的 Q 函数。这代表着，我们要为下一个状态 \(s'\) 找一个最好的 action，使得它在当前 weight \(\boldsymbol{\omega}\) 下的 utility 是最大的。这一步仍然很自然，相当于 \(\arg_Q \sup_a Q(s,a)\)，是经典的 bellman value iteration 思路。
• 然而，H 不仅 sup 了 a，还 sup 了 \(\boldsymbol{\omega}' \in \Omega\)。这一步的含义是，我们为 \(s'\) 找最好的 Q 时，不仅考虑当前策略 \(\pi(\cdot|s',\boldsymbol{\omega})\)，也去考虑其他策略 \(\pi(\cdot|s',\boldsymbol{\omega}')\)，说不定其他 weight \(\boldsymbol{\omega}'\) 下的策略更好呢？所以，最终得到了这样的 H 形式。
• \(\arg_{Q}\) 的含义是，这个算子返回的是使得上述 utility 最大的那个向量 Q 值 \(\boldsymbol{Q}(s', a', \boldsymbol{\omega}')\) 本身，而不是那个最大 utility。

抽象理解：H 不是在寻找一个单一的最优动作，而是在寻找当前 Q 函数所代表的整个解前沿的凸包。它允许算法“借用”在 weight \(\boldsymbol{\omega}'\) 下学到的最优 Q 值，来更新当前 weight \(\boldsymbol{\omega}\) 下的 Q 值。

然后，我们根据上述的 H，定义广义 bellman 最优性算子 \(\mathcal{T}\)：

\[(\mathcal{T}\boldsymbol{Q})(s, a, \boldsymbol{\omega}) := \boldsymbol{r}(s, a) + \gamma \mathbb{E}_{s' \sim \mathcal{P}(\cdot|s,a)} (\mathcal{H}\boldsymbol{Q})(s', \boldsymbol{\omega}) \]

不断让 Q ← TQ，就可以完成多目标下的 value iteration。这个公式的基本思想仍是 \(Q(s,a) \leftarrow r(s,a) + \gamma\sup_{a'} Q(s',a')\)，只不过使用了 H 算子。

3.3 理论保证（收敛性）

论文提供了三个关键定理，确保其方法的正确性：

• 定理1（不动点）：最优的多目标 Q 函数 \(\boldsymbol{Q}^*\) 是 \(\mathcal{T}\) 算子的不动点：\(\boldsymbol{Q}^* = \mathcal{T}\boldsymbol{Q}^*\)。
• 定理2（收缩性）：算子 \(\mathcal{T}\) 在伪度量 \(d\) 下是一个收缩映射：\(d(\mathcal{T}\boldsymbol{Q}, \mathcal{T}\boldsymbol{Q}') \leq \gamma d(\boldsymbol{Q}, \boldsymbol{Q}')\)。
• 定理3（广义巴拿赫不动点定理）：在完备的伪度量空间中，迭代应用 \(\mathcal{T}\) 会收敛到一个与 \(\boldsymbol{Q}^*\) 在度量 \(d\) 下等价的函数。

这些定理跟单目标的 value iteration 非常像。它们保证了，无论初始 Q 函数如何，通过反复应用 \(\mathcal{T}\) 进行更新，最终都能学到对于所有偏好 \(\boldsymbol{\omega}\) 都最优的 Q 函数。

3.4 具体的 loss function

在实践中，我们用一个神经网络 \(\boldsymbol{Q}(s, a, \boldsymbol{\omega}; \theta)\) 来近似 \(\boldsymbol{Q}\)，它的输出是 s、a、w，输出是 m 维的向量 Q 值。

通过最小化以下的 loss function，我们学习参数 \(\theta\)。

首先，更新目标 是 \(\boldsymbol{y} = \boldsymbol{r} + \gamma \arg_{Q} \max_{a', \boldsymbol{\omega}'} \boldsymbol{\omega}^\intercal \boldsymbol{Q}(s', a', \boldsymbol{\omega}'; \theta_{k}^{-})\)，其中 \(\theta_{k}^{-}\) 是目标网络的参数。

主损失 \(L^A\)（均方误差）：试图让 Q 函数的向量预测接近目标。

\[L^{A}(\theta) = \mathbb{E}_{s,a,\boldsymbol{\omega}} \left[ \| \boldsymbol{y} - \boldsymbol{Q}(s, a, \boldsymbol{\omega}; \theta) \|_2^2 \right] \]

这个 loss 确保 Q 函数能准确预测未来的向量回报，然而，优化起来可能很困难，因为解前沿包含大量离散点，导致损失函数可能非常不平滑。

辅助损失 \(L^B\)（效用误差）：直接最小化距离 \(d\)，让 Q 函数预测的标量 utility 接近目标 utility。

\[L^{B}(\theta) = \mathbb{E}_{s,a,\boldsymbol{\omega}} \left[ | \boldsymbol{\omega}^\intercal \boldsymbol{y} - \boldsymbol{\omega}^\intercal \boldsymbol{Q}(s, a, \boldsymbol{\omega}; \theta) | \right] \]

这个损失更平坦，更容易优化，但可能有很多解。

最终损失 \(L\)（homotopy optimization）：

\[L(\theta) = (1 - \lambda) \cdot L^{A}(\theta) + \lambda \cdot L^{B}(\theta) \]

其中 \(\lambda\) 从一个较小的值（如 0）逐渐增加到 1。这代表着，我们先优化 \(L^A\)，再优化 \(L^B\)；先确保 Q 的预测比较接近最有，再沿各个 weight 的方向细致地优化 utility。

（可能跟 DQN 一样，EQL 只适用于离散 action）

4 tricks

上述理论框架本身是优雅的，但要让其在实践中真正有效，论文依赖了几个关键的工程技巧：

1 homotopy 优化：

• 问题：直接优化 \(L^A\) 很难（地形崎岖），而直接优化 \(L^B\) 又太简单（地形平坦，解不唯一），可能导致模型收敛到一个在向量预测上不准确的解。
• 技巧：使用同伦优化，在训练初期主要使用 \(L^A\)，确保 Q 函数的向量预测朝着真实期望回报的方向发展。然后，逐渐引入 \(L^B\)，将优化过程“引导”至一个在 utility 上也最优的区域。

2 hindsight 经验回放：

• 问题：为了学习所有偏好下的策略，需要大量的交互数据。如果为每个偏好都收集数据，样本效率会极低。
• 技巧：从环境中采样一条轨迹（由某个随机偏好 \(\boldsymbol{\omega}_{\text{exec}}\) 生成）后，在更新时，从 replay buffer 取出该转移 \((s, a, \boldsymbol{r}, s')\)，并为其关联上一组随机采样的新 weight \(\{\boldsymbol{\omega}_1, ..., \boldsymbol{\omega}_{N_\omega}\}\)。然后，用这些新 weight 来计算损失并进行更新。实验中，每个转移样本会与 \(N_\omega = 32\) 个额外采样的偏好一起用于更新。
• 效果：一条在特定 weight 下收集的轨迹，可以被“重新解释”并用于更新其他 weight 下的 Q 函数，极大提高了样本效率。

3 对最优性滤波器 \(\mathcal{H}\) 的 mini-batch 近似：

• 问题：理论上，\(\mathcal{H}\) 需要在所有动作和所有 weight 上求极大值，这在连续或大的 weight 空间中是计算上不可行的。
• 技巧：在实践中，不在整个空间上计算，而是在每个训练 mini-batch 中，仅在**当前 batch 内出现的动作和 weight **上近似计算这个极大值。虽然这是一种近似，但实验证明它非常有效，并且随着训练的进行，batch 中的样本会逐渐覆盖最优解，使得近似越来越准确。

5 实验

5.1 task

这篇文章做了 4 个 task：

任务名称	state	action	一步 reward	任务描述
Deep Sea Treasure (DST)	智能体坐标 (x, y)	上、下、左、右	(时间惩罚, 宝藏价值)	在网格世界中导航，权衡时间成本与宝藏价值。
Fruit Tree Navigation (FTN)	当前节点坐标	进入左子树或右子树	(蛋白质, 碳水, 脂肪, 维生素, 矿物质, 水)	在二叉树中从根节点走到叶子节点，根据营养偏好选择最优“水果”。
Task-Oriented Dialog	对话状态（用户目标、历史等）	对话动作（询问、确认、提供信息等）	(对话轮数惩罚, 任务成功奖励)	在餐厅预订系统中，平衡对话成功率和对话简洁性。
Multi-Objective SuperMario	连续 4 帧游戏画面	7 个动作（左、右、跳、跑等组合）	(位置进度, 时间惩罚, 死亡惩罚, 收集硬币, 消灭敌人)	同时优化游戏进度、速度、生存、收集和战斗多个目标。

在学习阶段，agent 需要学习覆盖所有可能 weight 的策略，也就是去学习帕累托前沿。而在测试 / 适应阶段，我们可能直接给定 weight 执行策略，也可能在给定标量奖励的情况下，让 agent 快速推断出隐藏的 weight。

5.2 baselines

论文与三类基线方法进行对比（这是 deepseek 总结的，我没有细看）：

1. MOFQI：基于线性模型的传统多目标 Fitted Q-Iteration。缺点：无法处理高维状态（如游戏图像），可扩展性差。

2. CN+OLS：使用条件神经网络，外层用 Optimistic Linear Support 算法搜索 weight。缺点：在目标数量多（>3）时，OLS 计算成本极高，难以应用。

3. Scalarized：最强的基线，看起来也是最接近 EQL 的方法。使用一个神经网络，输入状态和偏好，输出标量 Q 值。通过标量化奖励（\(r_\omega = \boldsymbol{\omega}^\intercal \boldsymbol{r}\)）进行 Q 学习，并使用了 Hindsight Experience Replay 等技巧。缺点：更新时只考虑当前偏好，无法跨偏好共享信息，样本效率较低。

5.3 metrics

1. 覆盖率 (CR)：

   • 含义：衡量学习阶段找到所有潜在最优策略的能力。
   • 计算：类似于分类问题中的 F1 分数，是准确率（找到的策略中有多少是最优的）和召回率（所有最优策略中找到了多少）的调和平均数。

2. 平均效用 (UT)：在大量随机采样的偏好下，智能体获得的平均标量 utility。是 AE 的一个便捷代理指标。

3. 适应误差 (AE) / 适应质量 (AQ)：在适应阶段，对给定偏好 \(\boldsymbol{\omega}\)，智能体策略的效用与理论最优效用的差距。AE 越小越好，AQ 越大越好（\(AQ = 1/(1+\alpha \cdot AE)\)）。

4. 偏好推断准确率：反推的 ω 与真实 ω 的 L1 距离，越小越好。

5. （其实常用 MORL metrics 还有 hypervolume，但这篇看起来没有用）

5.4 具体实验结果

在四个 task 的所有主要指标上，EQL 均稳定优于或持平所有 baseline。

关键优势：

• 样本效率：在 FTN 任务中，要达到相同的性能，EQL 方法所需的交互数据（\(N_\omega\)）远少于Scalarized 方法。
• 可扩展性：当问题变复杂（如 FTN 树的深度从 5 增加到 7），EQL 的性能下降远小于 Scalarized 方法，表现出更好的鲁棒性和可扩展性。
• 偏好推断：在隐藏偏好测试中，Envelope 方法仅用 15 个回合（FTN） 或 100 个回合（SuperMario）就能较准确地推断出底层 weight，且比 Scalarized 方法更接近真实 weight。

5.5 细节实验设置

关键超参数与Trick：

• Hindsight Experience Replay：每个转移样本会与 \(N_\omega = 32\) 个额外采样的偏好一起用于更新。
• Double Q-learning & 目标网络：用于稳定训练，减少过高估计。
• Prioritized Experience Replay：根据时序差分误差（TD-error）的优先级进行采样，先学 TD-error 大的样本，加速学习。
• 探索策略：使用 \(\epsilon\)-greedy，\(\epsilon\) 从 0.5 线性衰减至 0。

网络结构：

• 向量 Q 网络：所有方法都使用同样架构的网络。使用 4 层全连接网络，输入为 state 向量和 weight 向量的拼接。输出层大小为 \(|\mathcal{A}| \times m\)（Envelope）或 \(|\mathcal{A}|\)（Scalarized）。
• MoA3C (for SuperMario)：使用卷积网络处理图像，后将特征与偏好拼接，再输入全连接层。

6 总结

本文提出的 Envelope Q-Learning 算法，通过定义向量 Q 函数和 envelope 最优算子，将经典 RL 的 bellman 优化拓展到多目标 RL 上，在理论上保证了多目标策略的收敛性。实践上，EQL 使用了homotopy 优化、double Q network、HER、PER 等 trick，加速策略收敛。个人认为，这是一个非常优雅的多目标 RL 框架，为 MORL 提供了强大的理论和算法工具。