递归与分治——实战

例1.整数划分问题

将正整数n表示成一系列正整数之和。

如 p（6）有11种划分：

　　6；

　　5 + 1；

　　4 + 2； 4 + 1 + 1；

　　3 + 3； 3 + 2 + 1； 3+ 1 + 1 + 1；

　　2+ 2 + 2； 2 + 2 + 1 + 1；2 + 1 + 1 + 1 + 1；

　　1 + 1 + 1 + 1 + 1 + 1；

　　

　　从上述可以看出 ：

　　1>对于p(6)来说，其都是不大于6的数字进行相加得到。

　　2>以5开头的有1条数据，以4开头的有2条，以3开头的有3条...，所以得到以m开头的就有6-m条；除了全部是1组成的数据。

　　

　　假设我们将 n 代替 6，在正整数n的所有不同的划分中，将最大正整数n1不大于m的划分个数记为P(n, m）;

　　对于6来说即为P(6, 6);

　　此时我们只需要确定n,m之间的区域规则划分即可。

 

　　1.当n = 1时或者m = 1时只有 P(n, m) = 1;

　　2.当m > n 时，P(n, m) = P(n , n);

　　3.当m = n 时 P(n, m) = 1 + P(n, n - 1);

　　4.当n > m > 1 时 P(n, m) = P(n, m - 1) + P(n - m, m);

 

　　对于第一点来说 指的就是1 + 1 + 1 + ...的情况。

　　对于第二点来说，因为不会存大于n的m组成的正整数之和为n; 

　　对于第三点来说，指的是自身n的这一条数据加上P(n, n - 1)的情况

　　对于第四条来说，假设 n = 6, m = 4；则P(6, 4) = P(6, 3) + P(2, 4)，我们可以看到P(6,3)是指m最大为3的所有数据划分，对于P(6,4)就只剩下了含有最大数为4的划分。

　　此时我们思考一个问题，一定含有4且4一定是小于6的，与4组成的数据划分之和为6，也就是说其他数据之和最大为6 - 4 = 2；

　　对于求含有4的划分数据之和可以转变为求所有之和为2的数据划分，即P(n - m, m)。所以P(n, m) = P(n, n - 1) + P(n - m, m);  

 

　　所以我们可以得到以下的递归式：

　　　　　　　　

 

 

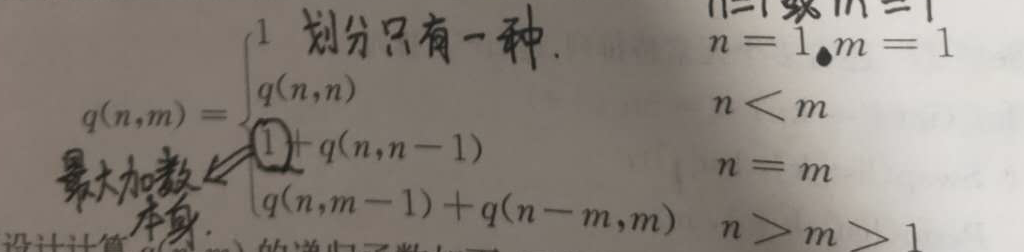
//整数划分问题
private int q(int n, int m) {
        if (n < 1 || m < 1) {
            return 0;
        }
        if (n == 1 || m == 1) {
            return 1;
        }
        if (n < m) {
            return q(n, n);
        }
        if (n == m) {
            return 1 + q(n, n - 1);
        }
        return q(n, m - 1) + q(n - m , m);
    }