第六章学习小结

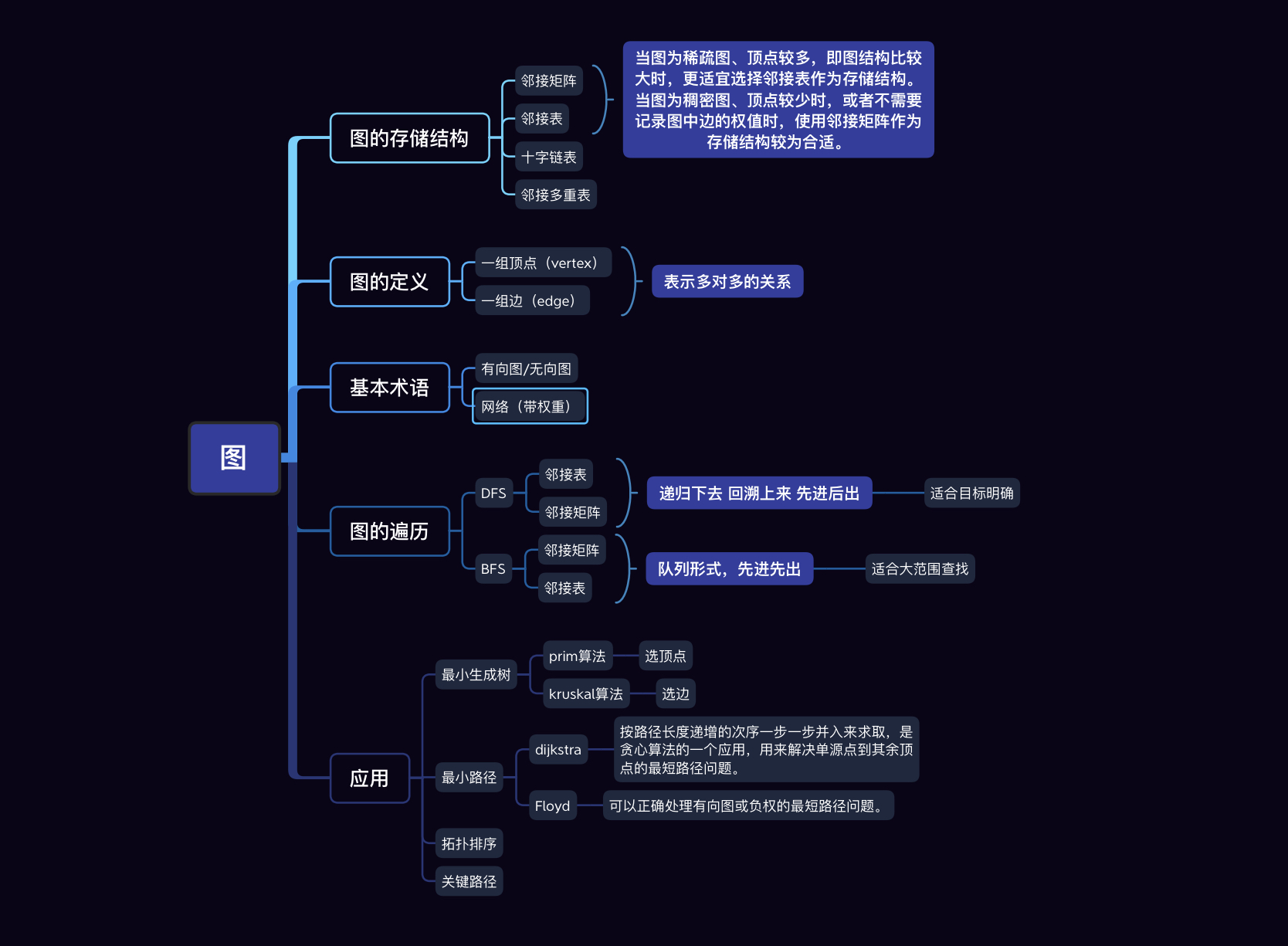
这章我们学了图的相关知识。

其中存储结构主要学了邻接矩阵和邻接表。

typedef struct
 {
     VerTexType vexs[MAX];
     ArcType arcs[MAX][MAX];
     int vexnum, arcnum;
  }AMGraph;//邻接矩阵

typedef struct ArcNode
 {
     int adjvex;
     struct ArcNode *next;
     OtherInfo info;
 }ArcNode;
 typedef struct VNode
 {
     VerTexType data;
     ArcNode *first;
 }VNode, AdjList[MAX];
 typedef struct
 {
     AdjList Vertices;
     int vexnum, arcnum;
 }ALGraph;//邻接表

 

还学习了深度优先搜索（DFS）和广度优先搜索（BFS）

 void DFS( Graph g,int v,int visited[])
  {
     /* 邻接矩阵存储，从顶点v出发，对图g进行深度优先搜索*/
     int i;
     cout << g.vexs[v];
     visited[v]=1; //标识v被访问过
     for(i=0;i<g.vexnum;i++); 
    {
         if( g.arcs[v][i]==1&&visited[i]==0)
         DFS(g,i,visited);//递归调用DFS
     }
 }
  
 void DFSTraverse(Graph g)
 { 
    
     int v;
     int visited[MVNUM];
     for(v=0;v<g.vexnum;v++)
     visited[v]=0; 
     for(v=0;v<g.vexnum;v++)
        if(visited[v]==0) 
           DFS(g,v,visited);
     
 }

void DFS(ALGraph g,int v,int visited[])
  {
      /*从顶点v出发，对图g进行深度优先搜索*/
      ArcNode *p;
      int w;
     cout << g.adjlist[v].data;
      visited[v]=1;//标记 
      p=g.adjlist[v].firstarc; //头指针 
      while(p)
     {
         w=p->adjvex; 
         if(visited[w]==0) 
             DFS(g,w,visited); //递归调用DFS
         p=p->nextarc; //找下一个邻接点
     }
 }
  
 void DFSTraverse(ALGraph g)
 { 
     
     int v;
     int visited[MAX_VERTEX_NUM];
    for(v=0;v<g.vexnum;v++)
         visited[v]=0; //初始化 
    for(v=0;v<g.vexnum;v++)
        if(visited[v]==0) 
             DFS(g,v,visited);     
 }

void BFS(graph& g, int v)//广度优先
 {
     cout << v << " ";
     visited[v] = true;
    queue<int> q;
     q.push(v);
     while (!q.empty())
    {
         int k = q.front();
         q.pop();
         for(int i=0; i<g.vexnum; i++)
             if (visited[i] == false && g.arcs[k][i] == 1)
             {
                cout << i << " ";
                 visited[i] = true;
                 q.push(i);
             }
     }
 }

#include<queue> 
void BFS(Graph G, int v)
{
    visited[v] = true;//标记是否访问     
     queue<int> q;//初始化
    q.push(v);
    
    while(!q.empty())
     {
         int u = q.front();
         q.pop();
         p = G.vertices[u].firstarc;
         while(p != NULL) 
         {
             w = p->adjvex; 
             if(!visited[w])
             {
                 visited[w] = true;
                 q.push(w); 
             }
             p = p->nextarc;     
         }
     }
 }

我们还学了最小生成树prim算法和kruskal算法

 

su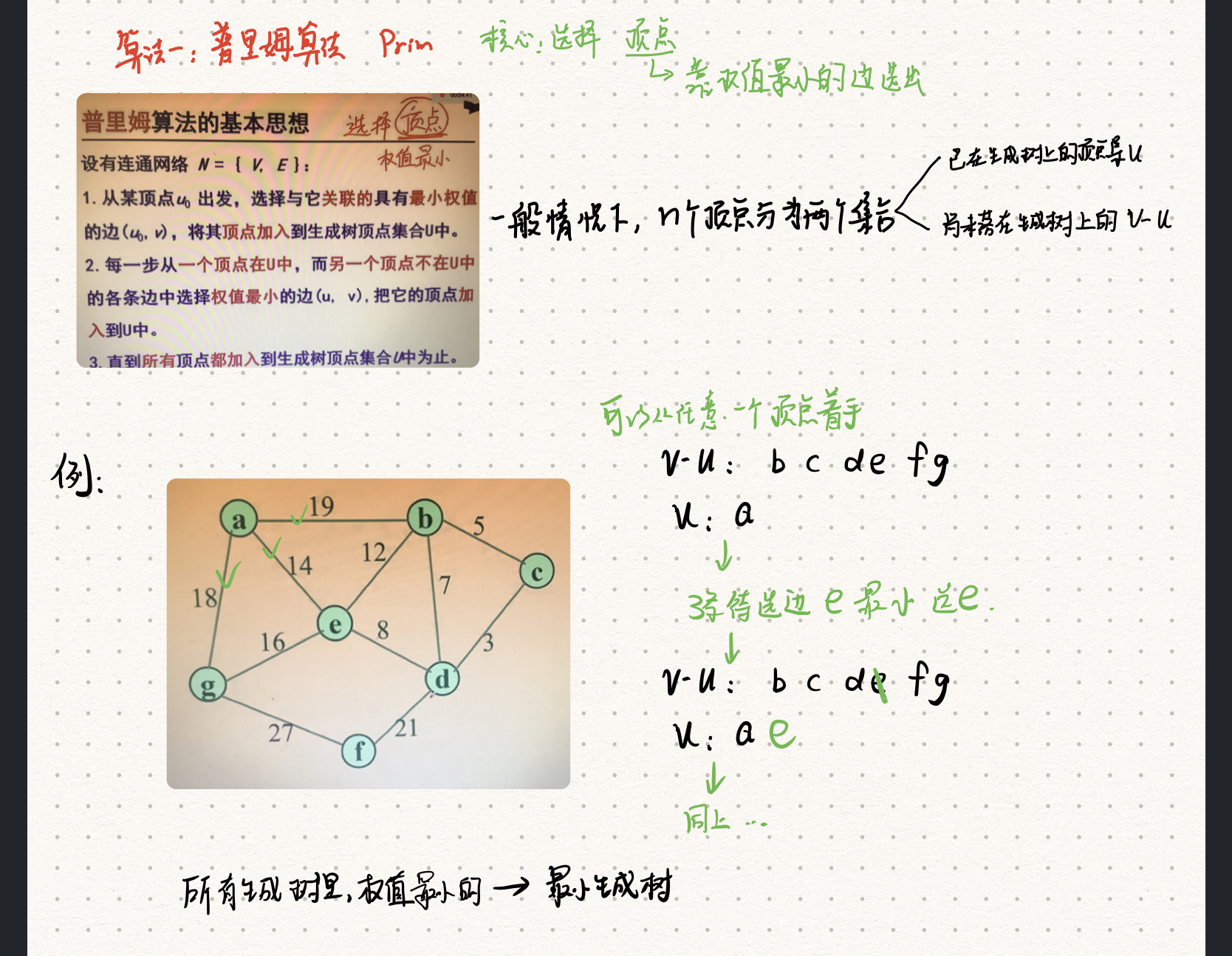

kruskal算法

1. 构造一个只有 n 个顶点，没有边的非连通图 T = { V, Æ }, 每个顶点自成一个连通分量

2. 在 E 中选最小权值的边,若该边的两个顶点落在不同的连通分量上，则加入 T 中；否则舍去，重新选择

3. 重复下去，直到所有顶点在同一连通分量上为止

 

 

 

 

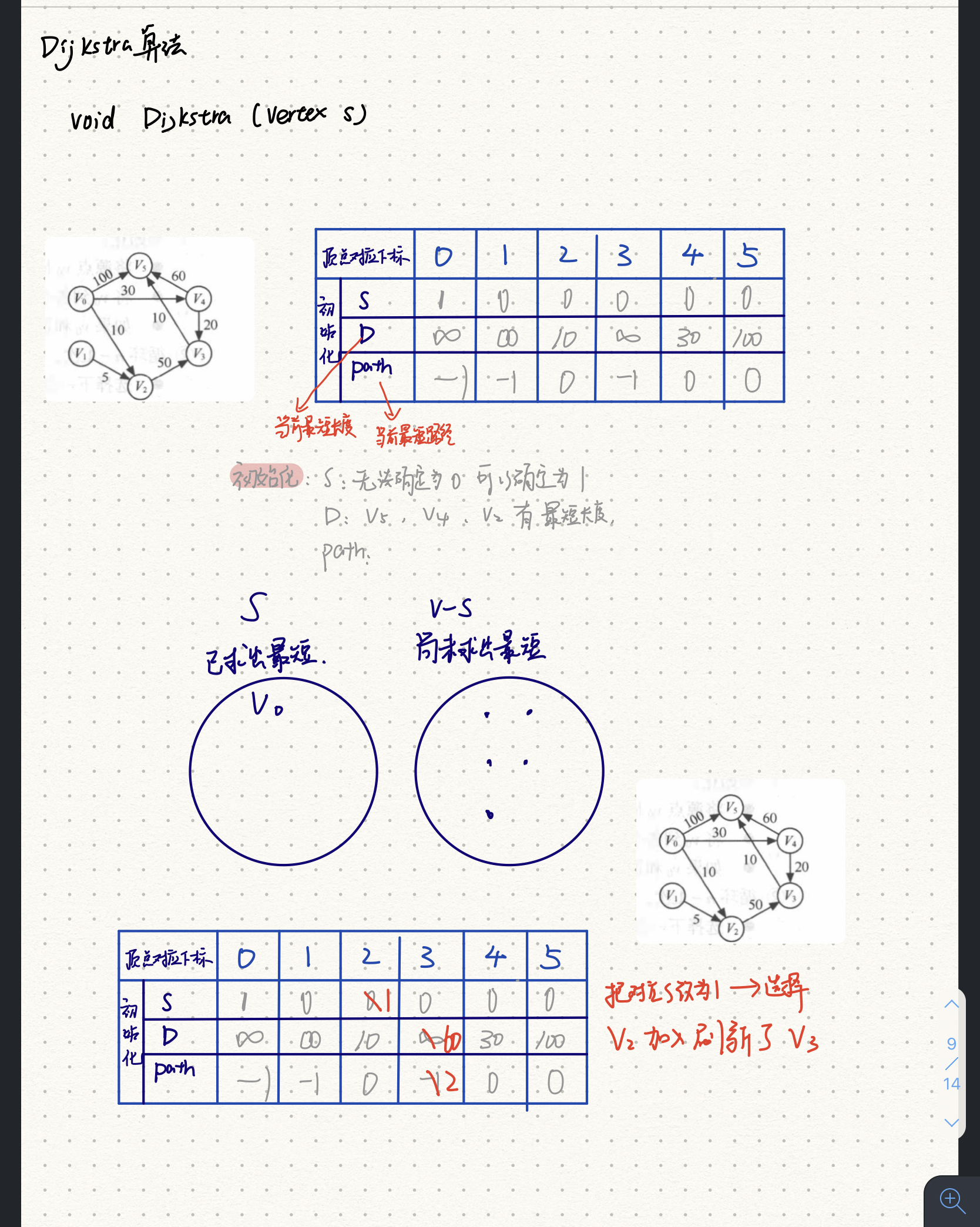
学习心得：这一章真的好难，上完课感觉会了，过一天再看前一天的笔记就不知道是什么了。还是我在数据结构上花的时间太少了，这个东西太繁琐了，一定要多多复习才对。

                 还有就是学习这章一定要仔细，之前的作业一不小心就会出错，还有看代码是也要仔细，一点点的不同就会让结果差之千里。