吴恩达深度学习笔记-4(深层神经网络)
深层神经网络
目前为止我们学习了只有一个单独隐藏层的神经网络的正向传播和反向传播,还有逻辑回归,并且你还学到了向量化,这在随机初始化权重时是很重要。
本周所要做的是把这些理念集合起来,就可以执行你自己的深度神经网络。
复习下前三周的课的内容:
1.逻辑回归,结构如下图左边。一个隐藏层的神经网络,结构下图右边:

注意,神经网络的层数是这么定义的:从左到右,由0开始定义,比如上边右图,\({x}{1}\)、\({x}{2}\)、\({x}_{3}\),这层是第0层,这层左边的隐藏层是第1层,由此类推。如下图左边是两个隐藏层的神经网络,右边是5个隐藏层的神经网络。
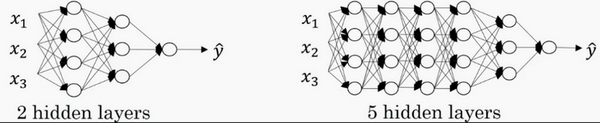
严格上来说逻辑回归也是一个一层的神经网络,而上边右图一个深得多的模型,浅与深仅仅是指一种程度。记住以下要点:
有一个隐藏层的神经网络,就是一个两层神经网络。记住当我们算神经网络的层数时,我们不算输入层,我们只算隐藏层和输出层。
但是在过去的几年中,DLI(深度学习学院 deep learning institute)已经意识到有一些函数,只有非常深的神经网络能学会,而更浅的模型则办不到。尽管对于任何给定的问题很难去提前预测到底需要多深的神经网络,所以先去尝试逻辑回归,尝试一层然后两层隐含层,然后把隐含层的数量看做是另一个可以自由选择大小的超参数,然后再保留交叉验证数据上评估,或者用你的开发集来评估。
我们再看下深度学习的符号定义:
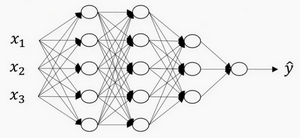
上图是一个四层的神经网络,有三个隐藏层。我们可以看到,第一层(即左边数过去第二层,因为输入层是第0层)有5个神经元数目,第二层5个,第三层3个。
我们用L表示层数,上图:\(L=4\),输入层的索引为“0”,第一个隐藏层\({n}^{[1]}=5\),表示有5个隐藏神经元,同理\({n}^{[2]}=5\),\({n}^{[3]}=3\),\({{n}^{[4]}}\)=\({{n}^{[L]}}=1\)(输出单元为1)。而输入层,\({n}^{[0]}={n}_{x}=3\)。
在不同层所拥有的神经元的数目,对于每层l都用\({a}^{[l]}\)来记作l层激活后结果,我们会在后面看到在正向传播时,最终能你会计算出\({{a}^{[l]}}\)。
通过用激活函数 \(g\) 计算\({z}^{[l]}\),激活函数也被索引为层数\(l\),然后我们用\({w}^{[l]}\)来记作在l层计算\({z}^{[l]}\)值的权重。类似的,\({{z}^{[l]}}\)里的方程\({b}^{[l]}\)也一样。
最后总结下符号约定:
输入的特征记作\(x\),但是\(x\)同样也是0层的激活函数,所以\(x={a}^{[0]}\)。
最后一层的激活函数,所以\({a}^{[L]}\)是等于这个神经网络所预测的输出结果。
前向传播
(略)
第1层,l=1:
第2层,l=2:
第3层,l=3:
第4层,l=4:
如果有m个训练样本,其向量化矩阵形式为:
第1层,l=1:
第2层,l=2:
第3层,l=3:
第4层,l=4:
综上所述,对于第l层,其正向传播过程的\(Z^{[l]}\)和\(A^{[l]}\)可以表示为:
其中l=1,⋯,L
计算过程中的矩阵维度确定
当实现深度神经网络的时候,其中一个我常用的检查代码是否有错的方法就是拿出一张纸过一遍算法中矩阵的维数。
\(w\)的维度是(下一层的维数,前一层的维数),即\({{w}^{[l]}}\): (\({{n}^{[l]}}\),\({{n}^{[l-1]}}\));
\(b\)的维度是(下一层的维数,1),即:
\({{b}^{[l]}}\) : (\({{n}^{[l]}},1)\);
\({{z}^{[l]}}\),\({{a}^{[l]}}\): \(({{n}^{[l]}},1)\);
\({{dw}^{[l]}}\)和\({{w}^{[l]}}\)维度相同,\({{db}^{[l]}}\)和\({{b}^{[l]}}\)维度相同,且\(w\)和\(b\)向量化维度不变,但\(z\),\(a\)以及\(x\)的维度会向量化后发生变化。
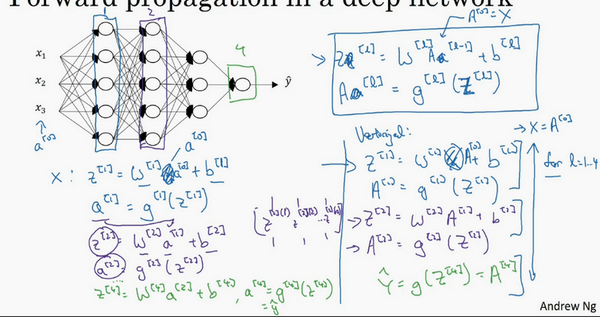
向量化后:
\({Z}^{[l]}\)可以看成由每一个单独的\({Z}^{[l]}\)叠加而得到,\({Z}^{[l]}=({{z}^{[l][1]}},{{z}^{[l][2]}},{{z}^{[l][3]}},…,{{z}^{[l][m]}})\),
\(m\)为训练集大小,所以\({Z}^{[l]}\)的维度不再是\(({{n}^{[l]}},1)\),而是\(({{n}^{[l]}},m)\)。
\({A}^{[l]}\):\(({n}^{[l]},m)\),\({A}^{[0]} = X =({n}^{[l]},m)\)
在你做深度神经网络的反向传播时,一定要确认所有的矩阵维数是前后一致的,可以大大提高代码通过率。下一节我们讲为什么深层的网络在很多问题上比浅层的好。
为什么要加深层次?
我们都知道神经网络能处理很多问题,而且效果显著。其强大能力主要源自神经网络足够“深”,也就是说网络层数越多,神经网络就更加复杂和深入,学习也更加准确。接下来,我们从几个例子入手,看一下为什么深度网络能够如此强大。
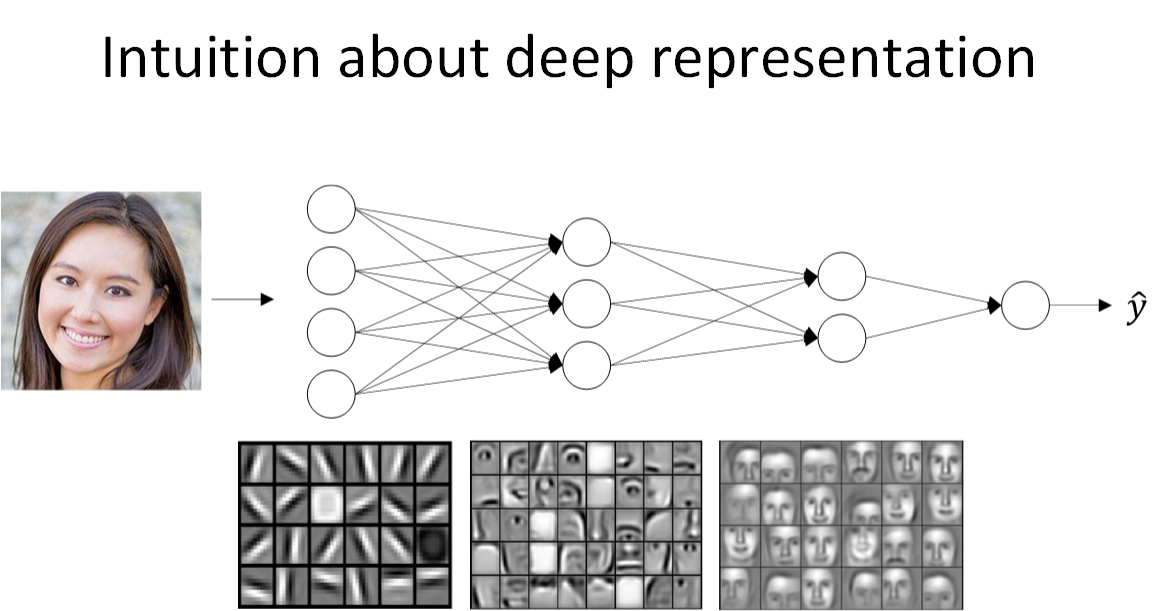
先来看人脸识别的例子,如下图所示。经过训练,神经网络第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘,即边缘检测。这样每个神经元得到的是一些边缘信息。神经网络第二层所做的事情就是将前一层的边缘进行组合,组合成人脸一些局部特征,比如眼睛、鼻子、嘴巴等。再往后面,就将这些局部特征组合起来,融合成人脸的模样。可以看出,随着层数由浅到深,神经网络提取的特征也是从边缘到局部特征到整体,由简单到复杂。可见,如果隐藏层足够多,那么能够提取的特征就越丰富、越复杂,模型的准确率就会越高。
语音识别模型也是这个道理。浅层的神经元能够检测一些简单的音调,然后较深的神经元能够检测出基本的音素,更深的神经元就能够检测出单词信息。如果网络够深,还能对短语、句子进行检测。记住一点,神经网络从左到右,神经元提取的特征从简单到复杂。特征复杂度与神经网络层数成正相关。特征越来越复杂,功能也越来越强大。
除了从提取特征复杂度的角度来说明深层网络的优势之外,深层网络还有另外一个优点,就是能够减少神经元个数,从而减少计算量。例如下面这个例子,使用电路理论,计算逻辑输出:
其中,⊕表示异或操作。对于这个逻辑运算,如果使用深度网络,深度网络的结构是每层将前一层的两两单元进行异或,最后到一个输出,如下图左边所示。这样,整个深度网络的层数是\(log_2(n)\),不包含输入层。总共使用的神经元个数为:
可见,输入个数是n,这种深层网络所需的神经元个数仅仅是n-1个。
如果不用深层网络,仅仅使用单个隐藏层,那么需要的神经元个数将是指数级别那么大。
比较下来,处理同一逻辑问题,深层网络所需的神经元个数比浅层网络要少很多。这也是深层神经网络的优点之一。
所以深度神经网络的这许多隐藏层中,较早的前几层能学习一些低层次的简单特征,等到后几层,就能把简单的特征结合起来,去探测更加复杂的东西。比如你录在音频里的单词、词组或是句子,然后就能运行语音识别了。同时我们所计算的之前的几层,也就是相对简单的输入函数,比如图像单元的边缘什么的。到网络中的深层时,你实际上就能做很多复杂的事,比如探测面部或是探测单词、短语或是句子。
有些人喜欢把深度神经网络和人类大脑做类比,这些神经科学家觉得人的大脑也是先探测简单的东西,比如你眼睛看得到的边缘,然后组合起来才能探测复杂的物体,比如脸。这种深度学习和人类大脑的比较,有时候比较危险。但是不可否认的是,我们对大脑运作机制的认识很有价值,有可能大脑就是先从简单的东西,比如边缘着手,再组合成一个完整的复杂物体,这类简单到复杂的过程,同样也是其他一些深度学习的灵感来源,之后的视频我们也会继续聊聊人类或是生物学理解的大脑。
Small:隐藏单元的数量相对较少
Deep:隐藏层数目比较多
深层的网络隐藏单元数量相对较少,隐藏层数目较多,如果浅层的网络想要达到同样的计算结果则需要指数级增长的单元数量才能达到。
除了这些原因,“深度学习”这个名字挺唬人的,这些概念以前都统称为有很多隐藏层的神经网络,但是深度学习听起来多高大上,太深奥了,这个词流传出去以后,这是神经网络的重新包装或是多隐藏层神经网络的重新包装,激发了大众的想象力。抛开这些公关概念重新包装不谈,深度网络确实效果不错,有时候人们还是会按照字面意思钻牛角尖,非要用很多隐层。但是开始解决一个新问题时,尽量先选择层数少的神经网络模型,这也符合奥卡姆剃刀定律(Occam’s Razor)。对于比较复杂的问题,再使用较深的神经网络模型。
构建深度NN的块
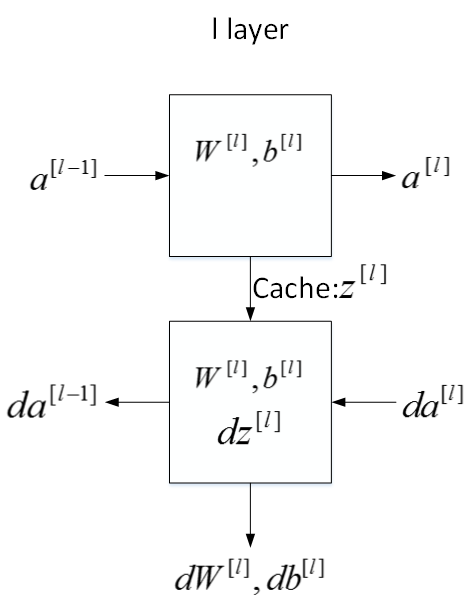
下面用流程块图来解释神经网络正向传播和反向传播过程。如下图所示,对于第l层来说,正向传播过程中:
输入:\(a^{[l-1]}\)
输出:\(a^{[l]}\)
参数:\(W^{[l]},b^{[l]}\)
缓存变量:\(z^{[l]}\)
反向传播过程中:
输入:\(da^{[l]}\)
输出:\(da^{[l-1]},dW^{[l]},db^{[l]}\)
参数:\(W^{[l]},b^{[l]}\)
刚才这是第l层的流程块图,对于神经网络所有层,整体的流程块图正向传播过程和反向传播过程如下所示:
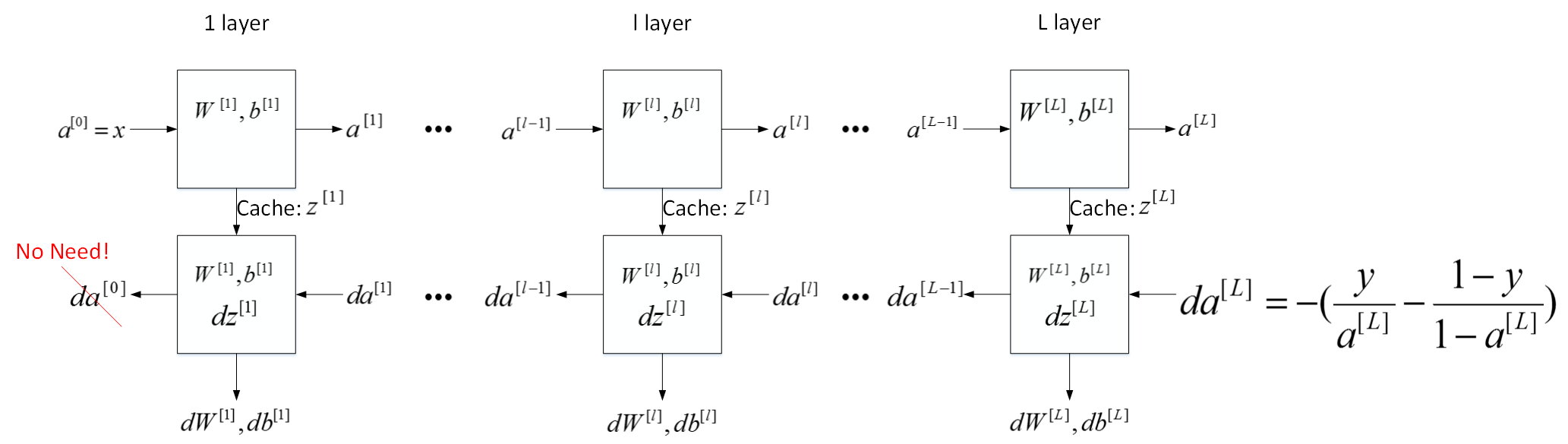
前向传播与反向传播
我们继续接着上一部分流程块图的内容,推导神经网络正向传播过程和反向传播过程的具体表达式。
首先是正向传播过程,令层数为第l层,输入是\(a^{[l-1]}\),输出是\(a^[l]\),缓存变量是\(z^[l]\)。其表达式如下:
m个训练样本,向量化形式为:
然后是反向传播过程,输入是\(da^{[l]}\),输出是\(da^{[l-1]},dw^{[l]},db^{[l]}\)。其表达式如下:
由上述第四个表达式可得\(da^{[l]}=W^{[l+1]T}\cdot dz^{[l+1]}\),将\(da^{[l]}\)代入第一个表达式中可以得到:
该式非常重要,反映了\(dz^{[l+1]}\)与\(dz^{[l]}\)的递推关系。
m个训练样本,向量化形式为:
参数与超参数
该部分介绍神经网络中的参数(parameters)和超参数(hyperparameters)的概念。
神经网络中的参数就是我们熟悉的\(W^[l]\)和\(b^[l]\)。而超参数则是例如学习速率\(α\),训练迭代次数N,神经网络层数L,各层神经元个数\(n^[l]\),激活函数\(g(z)\)等。之所以叫做超参数的原因是它们决定了参数\(W^[l]\)和\(b^[l]\)的值。在后面的第二门课我们还将学习其它的超参数,这里先不讨论。
如何设置最优的超参数是一个比较困难的、需要经验知识的问题。通常的做法是选择超参数一定范围内的值,分别代入神经网络进行训练,测试cost function随着迭代次数增加的变化,根据结果选择cost function最小时对应的超参数值。前面学习机器学习的时候学过所谓的一些方法来检测学习系统是否高效工作。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号