吴恩达深度学习笔记-2(编程基础)
神经网络的编程基础
逻辑回归
(省略学过的部分,只整理有些值得记录的地方,或者没学过的知识)
深度学习中的符号约定和之前学的机器学习当中的有些不同。
在深度学习中,逻辑回归的参数设为\(w\in{R^{n}}\),其输出值为\(\hat y=sigmoid(w^T+b)\),这个\(b\)类似于\(\theta_0\),那么对应而言\(w\in{R^{n}}\)就类似于\(\begin{bmatrix}{\theta_1}\\\\...\\\\{\theta_n}\end{bmatrix}\)
在深度学习中,有一个损失函数(loss function or error function),就比如线性回归的损失函数\(l=\frac{1}{2}{({\hat y}-y)}^2\),损失函数是针对单个训练样本而定义的。而之前讲的代价函数(成本函数),是针对全体训练样本而定义的,也就是说在损失函数前面加上求和,就变成了代价函数。
梯度下降
(省略)
导数
(省略)
计算图(Computation Graph)
(省略)
计算图中的导数计算
(省略)
反向传播
单个样本
深度学习中的反向传播和之前在机器学习中学的反向传播有形式上面的区别,但是深层原理是相通的,都是通过考虑权重对于整体输出结果误差的影响。特别记录在此。
假设样本只有两个特征\({{x}_{1}}\)和\({{x}_{2}}\)
有参数\({{w}_{1}}\)、\({{w}_{2}}\) 和\(b\)
因此\(z\)的计算公式为: \(z={{w}_{1}}{{x}_{1}}+{{w}_{2}}{{x}_{2}}+b\)
回想一下逻辑回归的公式定义: \(\hat{y}=a=\sigma (z)\) 其中\(z={{w}^{T}}x+b\) \(\sigma \left( z \right)=\frac{1}{1+{{e}^{-z}}}\)
损失函数: \(L( {{{\hat{y}}}^{(i)}},{{y}^{(i)}})=-{{y}^{(i)}}\log {{\hat{y}}^{(i)}}-(1-{{y}^{(i)}})\log (1-{{\hat{y}}^{(i)}})\)
代价函数: \(J\left( w,b \right)=\frac{1}{m}\sum\nolimits_{i}^{m}{L( {{{\hat{y}}}^{(i)}},{{y}^{(i)}})}\)
假设现在只考虑单个样本的情况,单个样本的代价函数定义如下:
\(L(a,y)=-(y\log (a)+(1-y)\log (1-a))\) 其中\(a\)是逻辑回归的输出,\(y\)是样本的标签值。
这里先复习下梯度下降法,\(w\)和\(b\)的修正量可以表达如下:
现在画出表示这个计算的计算图。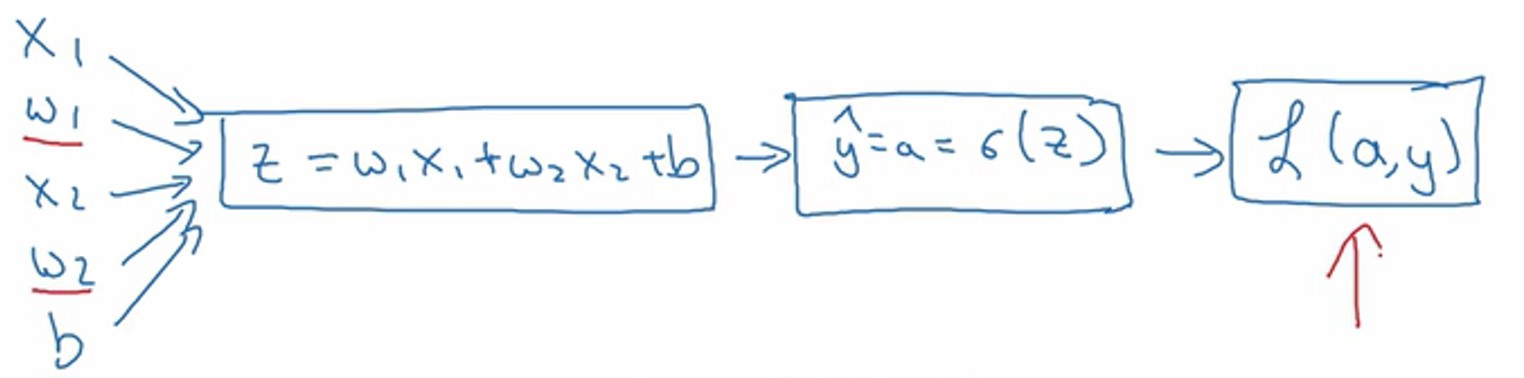
为了使得逻辑回归中代价函数\(L(a,y)\)最小化,我们需要做的是修改参数\(w\)和\(b\)的值。反向传播就是起到这么一个作用。
因为我们想要计算出的代价函数\(L(a,y)\)对参数\(w_1,w_2\)的偏导数
首先我们需要反向计算出代价函数\(L(a,y)\)关于\(a\)的偏导数
通过求导得到: \(\frac{\partial L(a,y)}{\partial a}=\frac{-y}{a}+\frac{(1-y)}{(1-a)}\)
再反向前进一步:\(\frac{\partial L}{\partial z}=a-y\)
根据链式法则有:\(\frac{\partial L(a,y)}{\partial z}=\frac{\partial L}{\partial z}=(\frac{\partial L}{\partial a})\cdot (\frac{\partial a}{\partial z})\)
并且\(\frac{\partial a}{\partial z}={(\frac{1}{1+e^{-z}})'}=\frac{e^{-z}}{(1+e^{-z})^2}=a\cdot (1-a)\), 而 \(\frac{\partial L}{\partial a}=(-\frac{y}{a}+\frac{(1-y)}{(1-a)})\)
因此将这两项相乘,得到:
再进行反向前进最后一步,也就是计算\(w_1,w_2\)和\(b\)变化对代价函数\(L\)的影响,有:
以上就是关于单个样本实例的梯度下降算法中参数更新一次的步骤。
多个样本
容易得到多个样本的偏导数如下:
将梯度下降表示到伪代码中,如下:
J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
z(i) = wx(i)+b;
a(i) = sigmoid(z(i));
J += -[y(i)log(a(i))+(1-y(i))log(1-a(i));
dz(i) = a(i)-y(i);
dw1 += x1(i)dz(i);
dw2 += x2(i)dz(i);
db += dz(i);
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db
for循环是非常慢的,所以需要引入向量化。
向量化
在逻辑回归中,需要去计算\(z={{w}^{T}}x+b\),\(w\)、\(x\)都是列向量。
假设,\(w\in {{\mathbb{R}}^{{{n}}}}\) , \(x\in{{\mathbb{R}}^{{{n}}}}\)
如果想使用非向量化方法去计算\({{w}^{T}}x\),需要用如下方式(python):
z=0
for i in range(n_x):
z += w[i]*x[i]
z += b
这是一个非向量化的实现,作为一个对比,向量化实现将会非常直接计算\({{w}^{T}}x\),代码如下:
z=np.dot(w,x)+b
PS:dot()返回的是两个数组的点积(dot product),如果处理的是一维数组(或者说向量),则得到的是两数组(向量)的內积;如果是二维数组(矩阵)之间的运算,则得到的是矩阵积
LR with 向量化
回顾逻辑回归的前向传播步骤。假设有 \(m\) 个训练样本,每个样本具有两个特征\(w_1,w_2\),令\(w=\begin{bmatrix}w_1\\\\w_2\end{bmatrix}\)
对第一个样本进行预测,需要这样计算 \(z\), \(z^{(1)}=w^{T}x^{(1)}+b\) 。然后计算激活函数 \(a^{(1)}=\sigma (z^{(1)})\) ,计算第一个样本的预测值\(y\) 。
然后对第二个样本进行预测,计算 \(z^{(2)}=w^{T}x^{(2)}+b\) , \(a^{(2)}=\sigma (z^{(2)})\) 。
然后对第三个样本进行预测,计算 \(z^{(3)}=w^{T}x^{(3)}+b\) , \(a^{(3)}=\sigma (z^{(3)})\) ,依次类推。
如果有\(m\)个训练样本,就需要这样做\(m\)次。
首先,令设计矩阵 \(X=\begin{bmatrix}x_2^1&&\cdots&&x_2^m\\\\x_1^1&&\cdots&&x_1^m\end{bmatrix}=\begin{bmatrix}x^1&&\cdots&&x^m\end{bmatrix}\)作为训练输入,这是一个 \(n\)行\(m\)列的矩阵。
容易得到\(w^T{X}=\begin{bmatrix}w_1&&w_2\end{bmatrix}\begin{bmatrix}x^1&&\cdots&&x^m\end{bmatrix}=\begin{bmatrix}w^T{x^1}&&&\cdots&&w^T{x^m}\end{bmatrix}\)
类似于Octave\MATLAB中学过的向量化,在python中是这样表示输出值的:
Z = np.dot(w.T,X) + b
等同于\(\begin{bmatrix}{w^T}{x^1}+b&&\cdots&&{w^T}{x^m}+b\end{bmatrix}=\begin{bmatrix}z^1&&\cdots&&z^m\end{bmatrix}\)
上面的代码中b是一个实数,但是当b与向量相加时,python会自动将b扩展为一个向量,这一特性称为python的广播。
梯度下降 with 向量化
令\(dz^{(1)}=a^{(1)}-y^{(1)}\),......,\(dz^{(m)}=a^{(m)}-y^{(m)}\)。
定义m维行向量\(dZ=[dz^{(1)} ,dz^{(2)} ... dz^{(m)}]\) ,所有的 \(dz\) 变量横向排列
再定义m维行向量\(A=a^{(1)},a^{(2)} ... a^{(m)}]\),和m维行向量\(Y=[y^{(1)} y^{(2)} ... y^{(m)}]\)
由此,可以计算 \(dZ=A-Y=[a^{(1)}-y^{(1)} ... a^{(m)}-y^{(m)}]=[dz^{(1)} ...dz^{(m)}]\)
定义向量\(db=\frac{\partial L(a,y)}{\partial b}\),不难发现$$db=\frac{1}{m}\sum_{i=1}{m}dz$$,之前的内容中,所有的\(dz^{i)}\)已经组成一个行向量\(dZ\)了,所以在Python中,容易想到\(db=\frac{1}{m}np.sum(dZ)\);
接下来定义\(dw=\frac{\partial L(a,y)}{\partial w}\),有\(dw=\frac{1}{m}XdZ^{T}\)其中,\(X\) 是一个行向量。因此展开后 $$dw=\frac{1}{m}(x{(1)}dz+x{(2)}dz+...+x{m}dz)$$ 。
因此可以仅用两行代码进行反向传播:$$db=\frac{1}{m}*np.sum(dZ)$$, $$dw=\frac{1}{m}XdZ^{T}$$。
那么整个前向传播与后向传播整合后的计算过程向量化表示如下:
\(Z = w^{T}X + b = np.dot( w.T,X)+b\)
\(A = \sigma( Z )\)
\(dZ = A - Y\)
\({{dw} = \frac{1}{m}Xdz^{T}\ }\)
\(db= \frac{1}{m}*np.sum( dZ)\)
\(w: = w - a*dw\)
\(b: = b - a*db\)
Python的广播
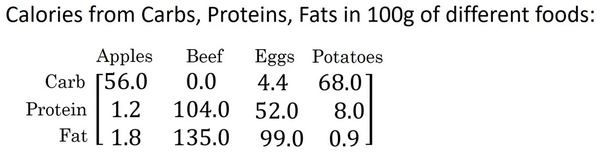
这是一个不同食物(每100g)中不同营养成分的卡路里含量表格,表格为3行4列,列表示不同的食物种类,从左至右依次为苹果,牛肉,鸡蛋,土豆。行表示不同的营养成分,从上到下依次为碳水化合物,蛋白质,脂肪。
现在想要计算不同食物中不同营养成分中的卡路里百分比。
计算苹果中的碳水化合物卡路里百分比含量,首先计算苹果(100g)中三种营养成分卡路里总和56+1.2+1.8 = 59,然后用56/59 = 94.9%算出结果。
可以看出苹果中的卡路里大部分来自于碳水化合物,而牛肉则不同。
对于其他食物,计算方法类似。首先,按列求和,计算每种食物中(100g)三种营养成分总和,然后分别用不用营养成分的卡路里数量除以总和,计算百分比。
那么,能否不使用for循环完成这样的一个计算过程呢?
假设上图的表格是一个4行3列的矩阵\(A\),记为 \(A_{3\times 4}\),接下来我们要使用Python的numpy库完成这样的计算。使用两行代码完成,第一行代码对每一列进行求和,第二行代码分别计算每种食物每种营养成分的百分比。
在jupyter notebook中输入如下代码,按shift+Enter运行,输出如下。
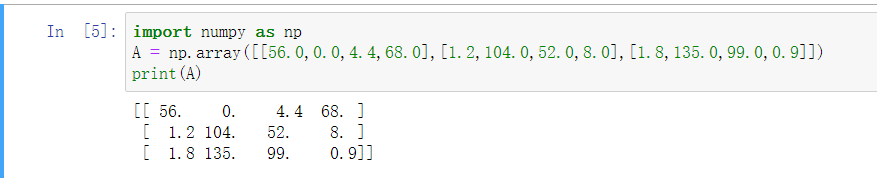
下面使用如下代码计算每列的和,可以看到输出是每种食物(100g)的卡路里总和。

其中sum的参数axis=0表示求和运算按列执行,之后会详细解释。
接下来计算百分比,这条指令将 \(3\times 4\)的矩阵\(A\)除以一个\(1 \times 4\)的矩阵,得到了一个 \(3 \times 4\)的结果矩阵,这个结果矩阵就是我们要求的百分比含量。
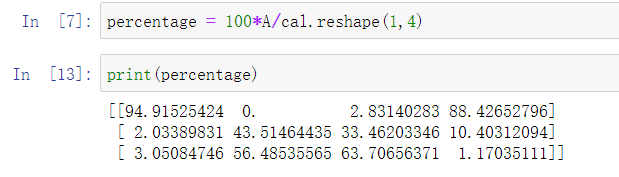
下面再来解释一下A.sum(axis = 0)中的参数axis。axis用来指明将要进行的运算是沿着哪个轴执行,在numpy中,0轴是垂直的,也就是列,而1轴是水平的,也就是行。
而第二个A/cal.reshape(1,4)指令则调用了numpy中的广播机制。这里使用 \(3 \times 4\)的矩阵\(A\)除以 \(1 \times 4\)的矩阵\(cal\)。技术上来讲,其实并不需要再将矩阵\(cal\) reshape(重塑)成 \(1 \times 4\),因为矩阵\(cal\)本身已经是 \(1 \times 4\)了。但是当我们写代码时不确定矩阵维度的时候,通常会对矩阵进行重塑来确保得到我们想要的列向量或行向量。重塑操作reshape是一个常量时间的操作,时间复杂度是\(O(1)\),它的调用代价极低。
那么一个 \(3 \times 4\) 的矩阵是怎么和 \(1 \times 4\)的矩阵做除法的呢?让我们来看一些更多的广播的例子。

在numpy中,当一个 \(4 \times 1\)的列向量与一个常数做加法时,实际上会将常数扩展为一个 \(4 \times 1\)的列向量,然后两者做逐元素加法。结果就是右边的这个向量。这种广播机制对于行向量和列向量均可以使用。
再看下一个例子。
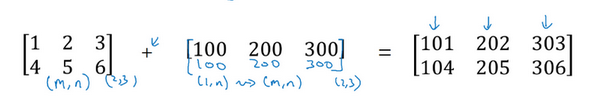
用一个 \(2 \times 3\)的矩阵和一个 \(1 \times 3\) 的矩阵相加,其泛化形式是 \(m \times n\) 的矩阵和 \(1 \times n\)的矩阵相加。在执行加法操作时,其实是将 \(1 \times n\) 的矩阵复制成为 \(m \times n\) 的矩阵,然后两者做逐元素加法得到结果。针对这个具体例子,相当于在矩阵的第一列加100,第二列加200,第三列加300。这就是在前一张幻灯片中计算卡路里百分比的广播机制,只不过这里是除法操作(广播机制与执行的运算种类无关)。
下面是最后一个例子
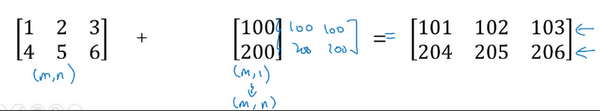
这里相当于是一个 \(m \times n\) 的矩阵加上一个 \(m \times 1\) 的矩阵。在进行运算时,会先将 \(m \times 1\) 矩阵水平复制 \(n\) 次,变成一个 \(m \times n\) 的矩阵,然后再执行逐元素加法。
广播机制的一般原则如下:

m*n的矩阵与行向量或列向量进行四则运算,会自动将行列向量扩展为能够符合数学运算要求的矩阵。
行列向量与实数进行四则运算,会自动将实数扩展为对应维度的行列向量。
Python中的向量注意事项
Python的特性允许你使用广播(broadcasting)功能,这是Python的numpy程序语言库中最灵活的地方。这是程序语言的优点,也是缺点。优点的原因在于它们创造出语言表达的灵活性,Python语言巨大的灵活性使得人们仅仅通过一行代码就能做很多事情。但是这也是缺点,由于广播机制巨大的灵活性,有时候由于对于广播的特点以及广播的工作原理这些细节不熟悉,就可能会产生很细微或者看起来很奇怪的bug。例如,如果将一个列向量添加到一个行向量中,按照常理它会报出维度不匹配或类型错误之类的错误,但是实际上会得到一个行向量和列向量的求和。
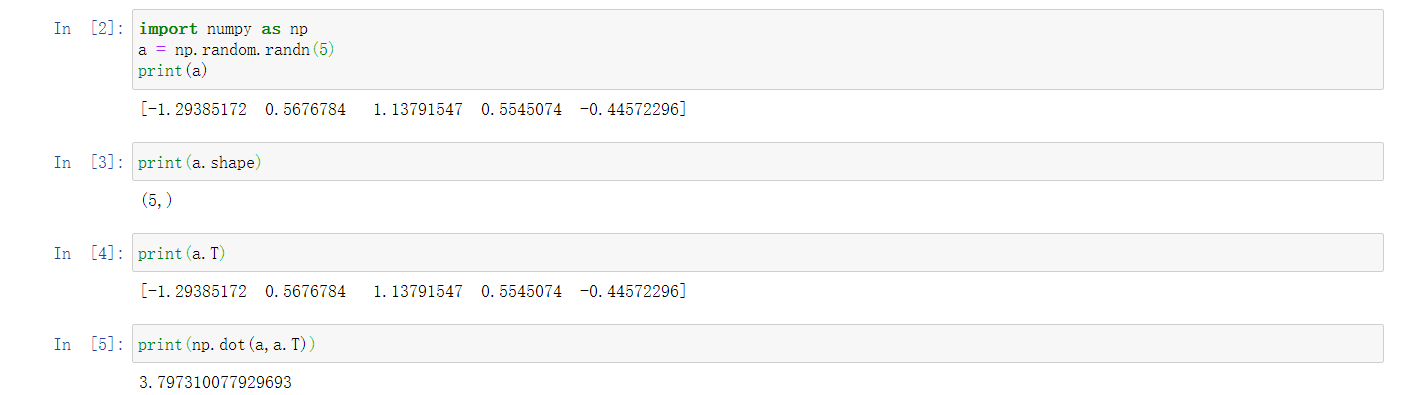
为了演示Python-numpy的一个容易被忽略的效果,特别是怎样在Python-numpy中构造向量,需要举一个例子。首先设置\(a=np.random.randn(5)\),这样会生成存储在数组 \(a\) 中的5个高斯随机数变量。之后输出 \(a\),从屏幕上可以得知,此时 \(a\) 的shape(形状)是一个\((5,)\)的结构。这在Python中被称作一个一维数组。它既不是一个行向量也不是一个列向量,这也导致它有一些不是很直观的效果。举个例子,如果我输出一个转置阵,最终结果它会和\(a\)看起来一样,所以\(a\)和\(a\)的转置阵最终结果看起来一样。而如果我输出\(a\)和\(a\)的转置阵的内积,你可能会想:\(a\)乘以\(a\)的转置返回给你的可能会是一个矩阵。但是如果这样做,只会得到一个数。
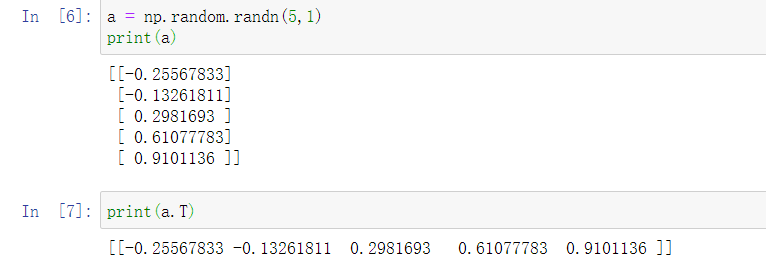
所以在编写神经网络时,不要使用shape为 (5,)、(n,) 或者其他一维数组的数据结构。相反,如果设置 \(a\) 为\((5,1)\),那么这就将置于5行1列向量中。在先前的操作里 \(a\) 和 \(a\) 的转置看起来一样,而现在这样的 \(a\) 变成一个新的 \(a\) 的转置,并且它是一个行向量。请注意一个细微的差别,在这种数据结构中,当我们输出 \(a\) 的转置时有两对方括号,而之前只有一对方括号,所以这就是1行5列的矩阵和一维数组的差别。

如果你输出 \(a\) 和 \(a\) 的转置的乘积,然后会返回给一个向量的外积,所以这两个向量的外积返回的是一个矩阵。
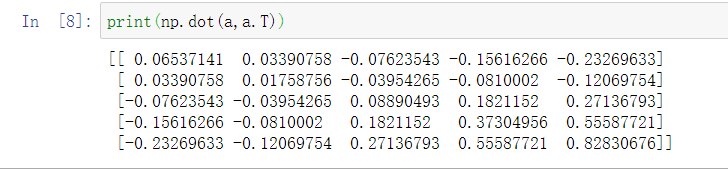
就我们刚才看到的,再进一步说明。首先我们刚刚运行的命令是这个 \((a=np.random.randn(5))\),它生成了一个数据结构\(a\),其中\(a.shape\)是\((5,)\)。这被称作 \(a\) 的一维数组,同时这也是一个非常有趣的数据结构。它不像行向量和列向量那样表现的很规整,这使得它会带来一些不明显的影响。所以在执行逻辑回归和编写神经网络时,最好避免使用这些一维数组。
相反,如果你每次创建一个数组,你都得让它成为一个列向量,产生一个\((5,1)\)向量或者你让它成为一个行向量,那么你的向量的行为可能会更容易被理解。所以在这种情况下,\(a.shape\)等同于\((5,1)\)。这种表现很像 \(a\),但是实际上却是一个列向量。同时这也是为什么当它是一个列向量的时候,你能认为这是矩阵\((5,1)\);同时这里 \(a.shape\) 将要变成\((1,5)\),这就像行向量一样。所以当你需要一个向量时,我会说用这个或那个(column vector or row vector),但绝不会是一维数组。
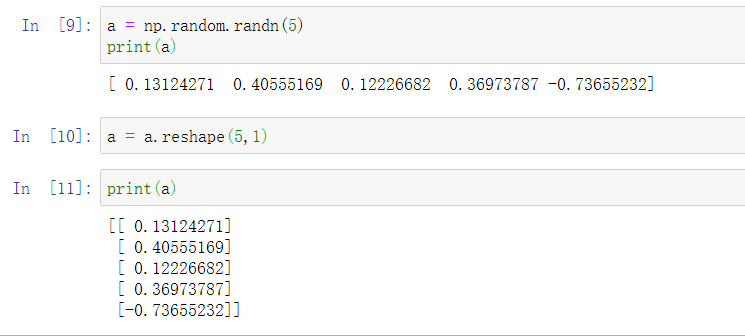
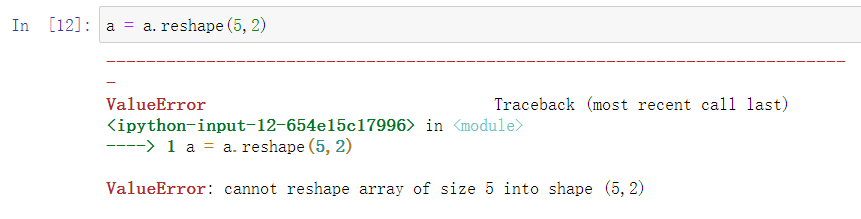
可以使用reshape命令使a转变为规整的向量。但只能是向量,如果是如下的想转为矩阵,则会报值的错误,因为没有正确的元素值。
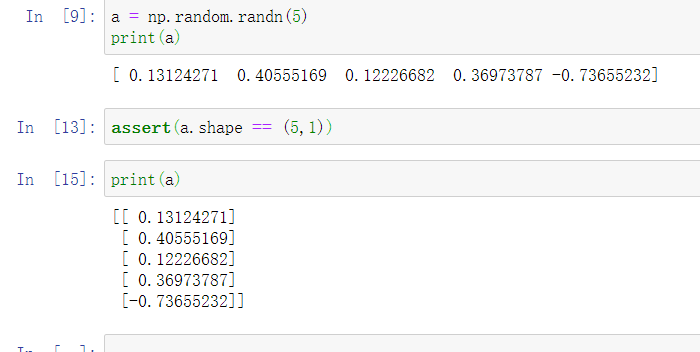
也可以通过assert命令来确保是向量。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号