吴恩达机器学习笔记-17(大规模机器学习)
大规模机器学习
所谓大规模机器学习,即是处理大数据集的方法。近年来机器学习技术飞速发展,其重要原因是现在有了海量的数据来训练算法。这一章学习能够处理海量数据的算法。
大规模机器学习有其特有的问题,具体来说是计算代价的问题。
假设现有一个样本m=100000000的数据集,这对于现代机器学习问题来说,这个数量级是很贴合实际情况的。
假设要用这个数据集去训练一个线性回归或者逻辑回归模型,训练过程中用到了梯度下降:
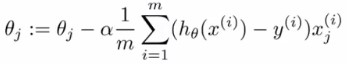
100000000次的迭代,计算代价显然非常之大。那么在用这个完整的数据集之前,不妨想想能否用这个数据集的一个子集来训练,比方说从中随机抽取1000个样本,组成一个子数据集,如果这个子数据集训练出来的模型效果也非常不错,那么就没有必要使用100000000个数据去训练。
考虑前面学过的学习曲线(learning curves),可以帮助我们判断是否有必要使用海量的数据集。
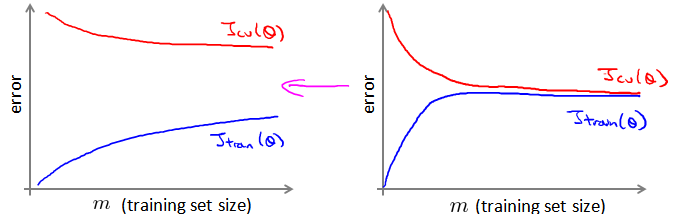
随机梯度下降
如果我们一定需要一个大规模的训练集,我们可以尝试使用随机梯度下降法来代替一般的梯度下降法(批量梯度下降)。
考虑之前学过的线性回归当中的普通梯度下降:

(右边是代价函数的图形)
对于这样一个梯度下降算法而言,在每次更新参数值的时候都会对m个样本求和,所以业内也常称之为批量梯度下降。如果m特别大,那么这个计算代价就会十分大,因为每次更新都会对m个实数求和
尝试使用随机梯度下降法来代替批量梯度下降法。
在随机梯度下降法中,新定义cost函数为一个单一训练实例的代价:
随机梯度下降算法为:首先对训练集随机“洗牌”,然后:
Repeat (通常迭代1-10次){
for \(i = 1:m\){
\(\theta:={\theta}{j}-\alpha\left( {h}{\theta}\left({x}^{(i)}\right)-{y}^{(i)} \right){{x}_{j}}^{(i)}\)
(j从0到n迭代)
}}
容易得到其中的\({(h_\theta(x^i))-y^i}x^i_j=\frac{\partial{cost(\theta,{(x^i,y^i)})}}{\partial\theta_j}\)
随机梯度下降算法在每一次计算之后便更新参数 \({{\theta }}\) ,这个计算是针对单个训练样本而言,而不需要首先将所有的训练集求和。在梯度下降算法还没有完成一次迭代时,随机梯度下降算法便已经走出了很远。
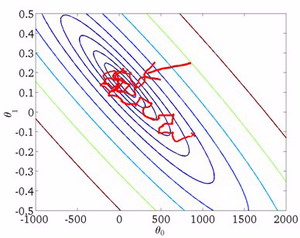
但是这样的算法存在的问题是,不是每一步都是朝着”正确”的方向迈出的。因此算法虽然会逐渐走向全局最小值的位置,但是可能无法站到那个最小值的那一点,而是在最小值点附近徘徊。
小批量梯度下降
小批量梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法,每计算常数\(b\)次训练实例,便更新一次参数 \({{\theta }}\)
小批量梯度下降某些时候可能比随机梯度下降更快。
回顾接触过的梯度下降算法:
- 批量梯度下降:每次迭代都要使用m个样本
- 随机梯度下降:每次迭代都只使用1个样本
- 小批量梯度下降:每次迭代使用b个样本,其中的b是被称作“小批量尺寸”的参数。通常情况下会令b=10,其常用的可选范围往往在2到100之间。
假设b=10,那么将得到训练集中的10个样本\({(x^i,y^i)},\cdots,{(x^i{+9},y^{i+9})}\)
更新过程应该为:
\(\theta:={\theta}{j}-\alpha\frac{1}{10}\sum\limits{k=i}^{i+9}\left( {h}{\theta}\left({x}^{(k)}\right)-{y}^{(k)} \right){{x}{j}}^{(k)}\)
这样一次迭代之后,将增加i的取值,令i=i+10,然后再取10个样本,这样一次一次进行下去。
具体过程,用伪代码表示如下:
b=1,m=1000
for \(i = 1,11,21,31,...,991\){
\(\theta:={\theta}{j}-\alpha\frac{1}{10}\sum\limits{k=i}^{i+9}\left( {h}{\theta}\left({x}^{(k)}\right)-{y}^{(k)} \right){{x}{j}}^{(k)}\)
(for \(j=0,...,n\))
} }
通常我们会令 \(b\) 在 2-100 之间。这样做的好处在于,我们可以用向量化的方式来循环 \(b\)个训练实例,如果我们用的线性代数函数库比较好,能够支持平行处理,那么算法的总体表现将不受影响(与随机梯度下降相同)。
随机梯度下降收敛
这一节学习关于随机梯度下降中,对于算法的调试以及学习速率\(\alpha\)的选取。
在批量梯度下降中,我们可以把\(J_{train}(\theta)\)绘制成有关于迭代次数的函数(以迭代次数为横轴,函数值为纵轴),根据图表来判断梯度下降是否收敛。
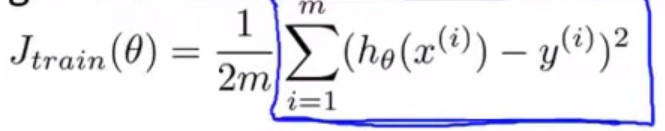
但是如果样本特别庞大, 这个方法就不可行了,因为每求一次代价函数值,就要求m个实数的和,计算代价高,运算速度慢
而在随机梯度下降中:
- 在每一次更新 \({{\theta }}\) 之前都计算一次\(cost\left( \theta, \left( {x}^{(i)} , {y}^{(i)} \right) \right) = \frac{1}{2}\left( {h}_{\theta}\left({x}^{(i)}\right)-{y}^{{(i)}} \right)^{2}\)
- 然后每\(x\)次迭代后,求出这\(x\)次对训练实例计算代价的平均值,然后绘制这些平均值与\(x\)次迭代的次数之间的函数图表。

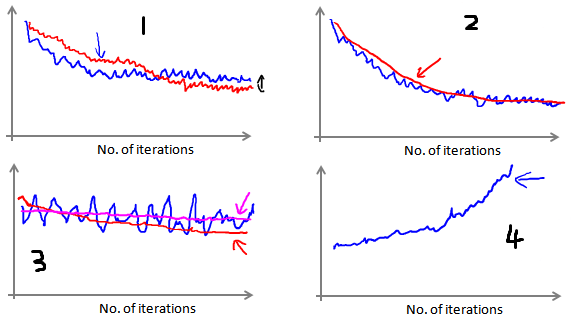
在图1中,可能会得到如蓝色线所示的曲线,此时减小学习速率\(α\),可能会得到红色线,下降更慢,也许会收敛到一个更好的值,但是在实际应用当中,这两种区别是可以忽略不计的。
在图2中,增大每组样本中的样本数量,比如说一组样本从1000个增大到5000个,也许会使曲线更加平滑。
在图3中,可能会得到一个颠簸不平但是不会明显减少的函数图像(如上面左下图中蓝线所示)。我们可以增加\(α\)来使得函数更加平缓,也许便能看出下降的趋势了(如上面左下图中红线所示);或者可能函数图表仍然是颠簸不平且不下降的(如洋红色线所示),那么我们的模型本身可能存在一些错误。
在图4中,可能根本得不到一个呈现收敛趋势的曲线,那么此时需要减小学习速率\(α\)。
在随机梯度下降中,参数\(\theta\)会从某个点开始,然后曲折地向全局最优解收敛,但是并不是每次都能够准确收敛到最优值,有可能最后会在最优解附近徘徊。
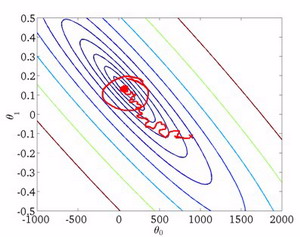
那么最后得到的只是一个全局最小值的接近值,而不是真正的全局最小值。
在大多数随机梯度下降算法的例子当中,学习速率\(α\)都是一个常数,如果出现了这样徘徊的情况,可以考虑让学习速率随迭代次数的增加而缓慢逐渐减小,令\(\alpha=\frac{常数1}{迭代次数+常数2}\)
在线学习(online learning)
在线学习机制可以模型化一些问题。就是说,有连续的一波数据或者连续的数据流,想用算法从中学习的这类问题。
现如今,有许多大型网站或者许多大型网络公司,使用不同版本的在线学习机制算法,从大批涌入又离开网站的用户身上进行学习。特别要提及的是,如果有一个由连续的用户流引发的连续的数据流进入自己的网站,我们能做的是使用一个在线学习机制,从数据流中学习用户的偏好,然后使用这些信息来优化一些关于网站的决策。
假设我们提供一个运输服务,并且有一个网站,用户来咨询有关把包裹从A地运到B地的服务。用户登录我们的网站,然后告诉我们,他们想从哪里寄出包裹,以及包裹要寄到哪里去,也就是发出地与目的地,然后我们的网站开出运输包裹的的服务价格,类似于现在的在线寄件服务。用户根据开出的价格,也许会选择我们的服务,也许不会选择我们的服务。如果选择了,那么就是一个正类(y=1),反之是负类(y=0)。
所以我们会想要用一个学习算法,来优化我们提供的价格,使用户更容易接受它。
假设我们获取了描述用户特点的特征,例如用户快递的发出地,目的地,以及我们的报价,要做的就是,用学习算法来预测用户选择我们提供的快递服务的几率(\(p(y=1|x;\theta)\)),根据这个几率来优化我们的报价。这里可以用神经网络、逻辑回归或者其他的一些分类问题的算法,这里将以逻辑回归作为例子来讲解。
现在假定有一个正在运作的网站,在线学习算法要做的就是:
一直重复迭代 (只要网站在运行) {
获取有关当前登录用户的数据对\(\left(x,y\right)\)
用数据更新\(\theta\)
\(\theta:={\theta}{j}-\alpha\left( {h}{\theta}\left({x}\right)-{y} \right){{x}_{j}}\) (for \(j=0:n\)) }
在线学习没有固定的数据集这一概念,取而代之的是不断更新的数据流。
获取一个样本,用这个样本进行学习,然后丢弃这个样本,不再使用它,这就是为什么一次只处理一个样本。
因为有一个连续不断的数据流输入进学习系统当中,所以可以说能够获取的数据是无限的,那么或许就没必要多次使用一个样本。如果只有少量的用户,当然最好还是用一个固定的数据集。
在线学习的好处在于,算法可以很好的适应用户的倾向性,可以针对用户群的当前行为不断地更新模型以适应最新的用户群。
另一种在线学习的例子是商品搜索:
用户搜索“安卓 手机 1080p 摄像头”,有100部手机在数据库当中,网站被设计为当用户键入搜索命令,会返回10部最合适的手机给用户,网站提供方就会希望有学习算法来使得能在100部手机中找到哪10部手机是应该反馈给用户的,是最佳的回应。
对于每部手机,以及一个给定的用户搜索命令,可以构建一个特征向量x,包含了手机的特点,用户的搜索与这部手机的类似程度有多高等等,如果用户点击了链接则是正类(y=1),反之为负类(y=0)。
通过学习算法来计算用户点击的概率\(p(y=1|x;\theta)\),这种问题其实被称之为,点击率预测学习问题(predicted click-through rate,CTR)
从100部手机中,选择10部用户最有可能点击的手机,这就是一个非常合理的方法。
由于要返回10个数据,那么这样一来,每一个用户访问网站,都会得到10个数据样本(10个(x,y)数据对)。因为对于这10部我们选择要展示给用户的手机,从每一部手机得到一个特征向量x,对于这10部手机中的每一个,还会得到对应地y的取值,这个取值由用户是否点击而决定。
然后用在线学习算法,对这10个样本利用梯度下降也好,其他算法也好,更新参数\(\theta\),之后就可以丢弃掉这些样本。
其他一些应用例子有:新闻定向推荐,商品推荐等等。
在线学习算法与随机梯度下降算法非常类似,唯一的区别的是,在线学习不会使用一个固定的数据集,要做的是获取一个用户样本,从那个样本中学习,然后丢弃那个样本并继续下去。如果对某一种应用有一个连续的数据流,这样的算法可能会非常值得考虑。
在线学习其实更像是一种思想,利用现代网络技术的特点,高效收集数据,进行机器学习。
MapReduce和数据并行
MapReduce和数据并行对于大规模机器学习问题而言是非常重要的概念。之前提到,如果我们用批量梯度下降算法来求解大规模数据集的最优解,我们需要对整个训练集进行循环,计算偏导数和代价,再求和,计算代价非常大。如果我们能够将我们的数据集分配给不多台计算机,让每一台计算机处理数据集的一个子集,然后我们将计所的结果汇总在求和。这样的方法叫做MapReduce。
有这样一个例子,现有样本400个,考虑批量梯度下降:
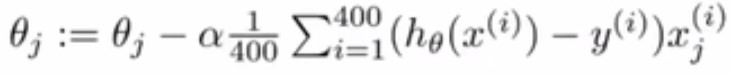
假设有4台计算机,如果要使用MapReduce思想,会将数据集(400个样本)分为4份,每份100个。
第一台计算机要做的就是计算\(temp^1_j=\sum^100_{i=1}{(h_\theta(x^i)-y^i)}x^i_j\)
第二台计算机要做的就是计算\(temp^2_j=\sum^200_{i=101}{(h_\theta(x^i)-y^i)}x^i_j\)
第三台计算机要做的就是计算\(temp^3_j=\sum^300_{i=201}{(h_\theta(x^i)-y^i)}x^i_j\)
第四台计算机要做的就是计算\(temp^4_j=\sum^400_{i=301}{(h_\theta(x^i)-y^i)}x^i_j\)
最后将这四个中间值重新放到一起:
要进行并行计算,要做的就是把训练集均匀或者尽量均匀地根据计算机数量分为n份,最后将n个结果传送给一个中心服务器将结果汇总。
总的来说,只要学习算法可以表示成一系列的求和,或者表示成在训练集上对函数的求和形式,那么MapReduce思想就是适用的。
多核处理器的单机MapReduce
现在的MapReduce其实是可以单机运行的,因为现在很多计算机都是多核处理器。只需要把训练集分成n份,发给n个核心,再把每个部分加起来得到和,把MapReduce看成是单机中的不同核心的并行处理,而不是多台机器并行,这样的好处在于不用担心通信传输问题,因为在于中心服务器的通信传输过程当中,不可避免地会有延迟,甚至会出现其他网络安全问题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号