吴恩达机器学习笔记-13(聚类)
聚类
无监督学习使用的是无标签的数据,研究的是数据之间隐藏的内在结构。
K-Means算法(K均值聚类算法)
因此,我们希望有一种算法能够自动地将这些数据,分成有紧密关系的子集(簇,cluster)。
K-Means算法是现在最为广泛运用的聚类算法。下面通过图像具体说明执行过程:
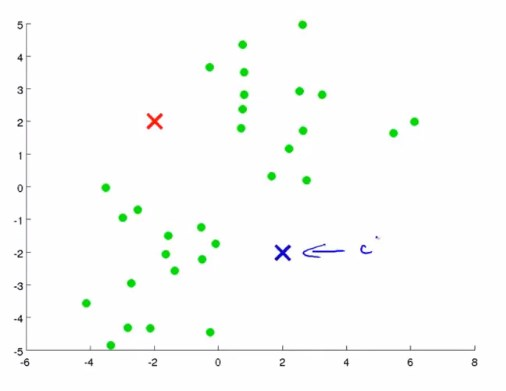
有这样一个数据集,首先随机指定两个聚类中心,如图所示。
K-Means算法是一个迭代算法,一次迭代中要做的事只有两件:1. 簇分配。2. 移动中心
第一件事情簇分配,就是指,对每个样本,也就是图中的绿点。根据每个绿点是离红色中心更近还是离蓝色中心更近,然后将绿点分配给最近的中心。
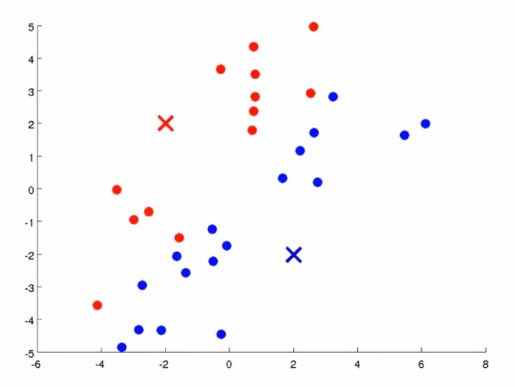
第二件事情是,移动聚类中心,也就是红色蓝色的叉。要做的就是,找出所有红色的点,算出红点的均值,然后将红中心移动到均值的位置(这个均值是一个向量),对蓝点做类似操作。
然后继续进行迭代,直到中心不再移动。
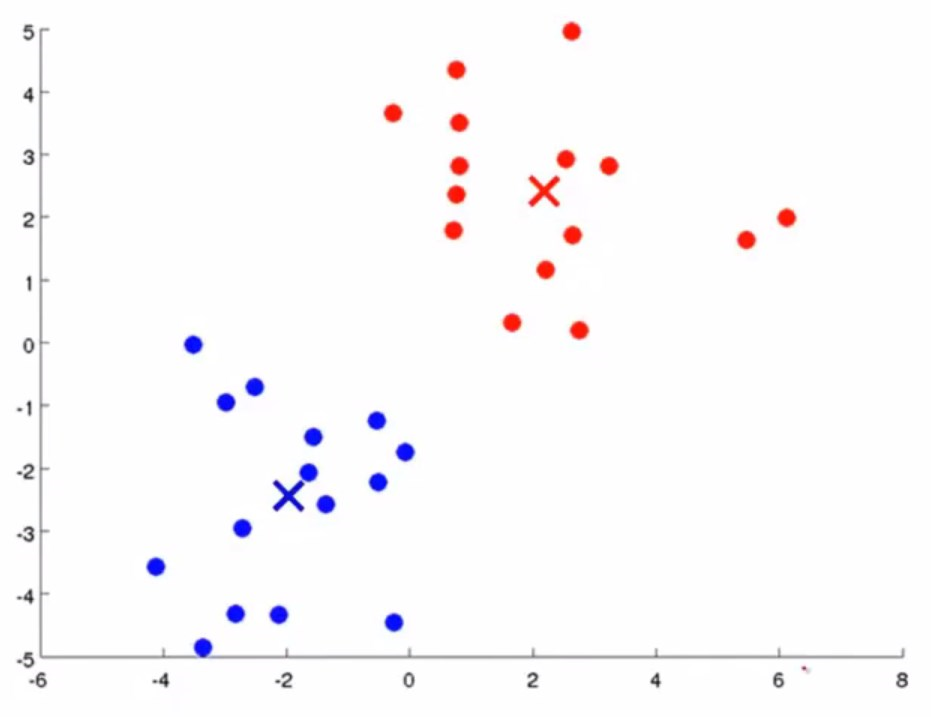
首先,我们需要确定我们希望在数据集中分出K个簇,输入m个样本\({x^1,...,x^m}\)
在K-Means算法中,\(x^i\)是一个n维向量。(按照惯例,其中\(x^i_0=1\))
那么从伪代码的角度讲:
随机初始化K个聚类中心\(\mu_1,...,\mu_K\)(每个都是n维向量)
REPEAT{
for i = 1 to m
\(c^i := 离x^i最近的聚类中心的索引(索引值从1 to K)\)
for k = 1 to K
\(\mu_k:=分配给簇k的 所有点的均值\)
}
第二步那里的\(c^i\),本意指的是样本和中心之间的最小欧氏距离,也就是范数\(||x^i-\mu_{k}||\)。但是按照惯例,我们会令\(c^i=min{(||x^i-\mu_{k}||)}^2\)
最后一步的所谓均值,其实也就是分配给簇k的所有点相加求均值(注意那些点都是向量,所以是几个向量相加求的均值)
对于本身分离性不明显的数据集,K-Means也可以解决,譬如下面这个例子:
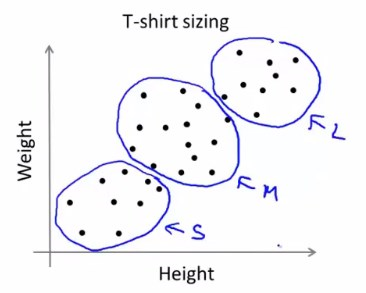
对于一个T恤制造商来说,需要分类这样一个由身高体重组成的数据集,运用K-Means算法可以仍然可以分成三簇。
K-Means的优化目标函数(代价函数)
之前学习的各种监督学习算法,都有其各自的优化目标函数(也可以说是代价函数)。通过优化这个函数,求得参数\(\theta\),使得模型趋于最优。
类似地,K-Means算法也有他自己的优化目标函数。
首先给出如下定义:
\(c^i = 样本x^i当前所属的簇的索引(索引值从1 to K)\)(譬如,如果\(x^i\)属于簇5,那么\(c^i=5\))
\(\mu_k = 聚类中心k\)
\(\mu_{c^i} = 样本x^i所属的簇的聚类中心\)
那么可以给出K-Means算法的优化目标函数(也可以叫做失真代价函数或者K-Means的失真):
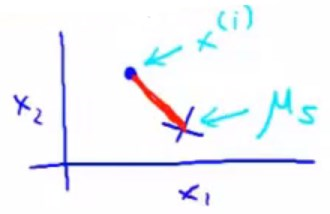
容易发现,在K-Means的迭代过程中,其实就在对函数进行最小化处理
REPEAT{
1 for i = 1 to m
2 \(c^i := 离x^i最近的聚类中心的索引(索引值从1 to K)\)
3 for k = 1 to K
4 \(\mu_k:=分配给簇k的所有点的均值\)
}
对于第1、2步而言,就是在用参数\(c^i\)对函数进行最小化,直观上来说,将\(x^i\)分配给离它最近的簇,自然会使得它到簇中心的距离平方最小。
对于第3、4步而言,就是在用参数\(\mu_k\)对函数进行最小化,因为从直观上来说,中心最终会离各自的簇越来越近,所以距离平方会越来越小。
避免局部最优以及聚类中心初始化
在进行K-Means迭代之前,需要做的是聚类中心的初始化。
一般来说聚类中心数K<样本数m,然后随机选择K个训练样本,令\(\mu_1,...,\mu_K\)分别等于这K个样本,就完成了聚类中心的初始化。
那么容易想到,因为随机化结果的不同,K-Means最终也许会得到不同的结果。
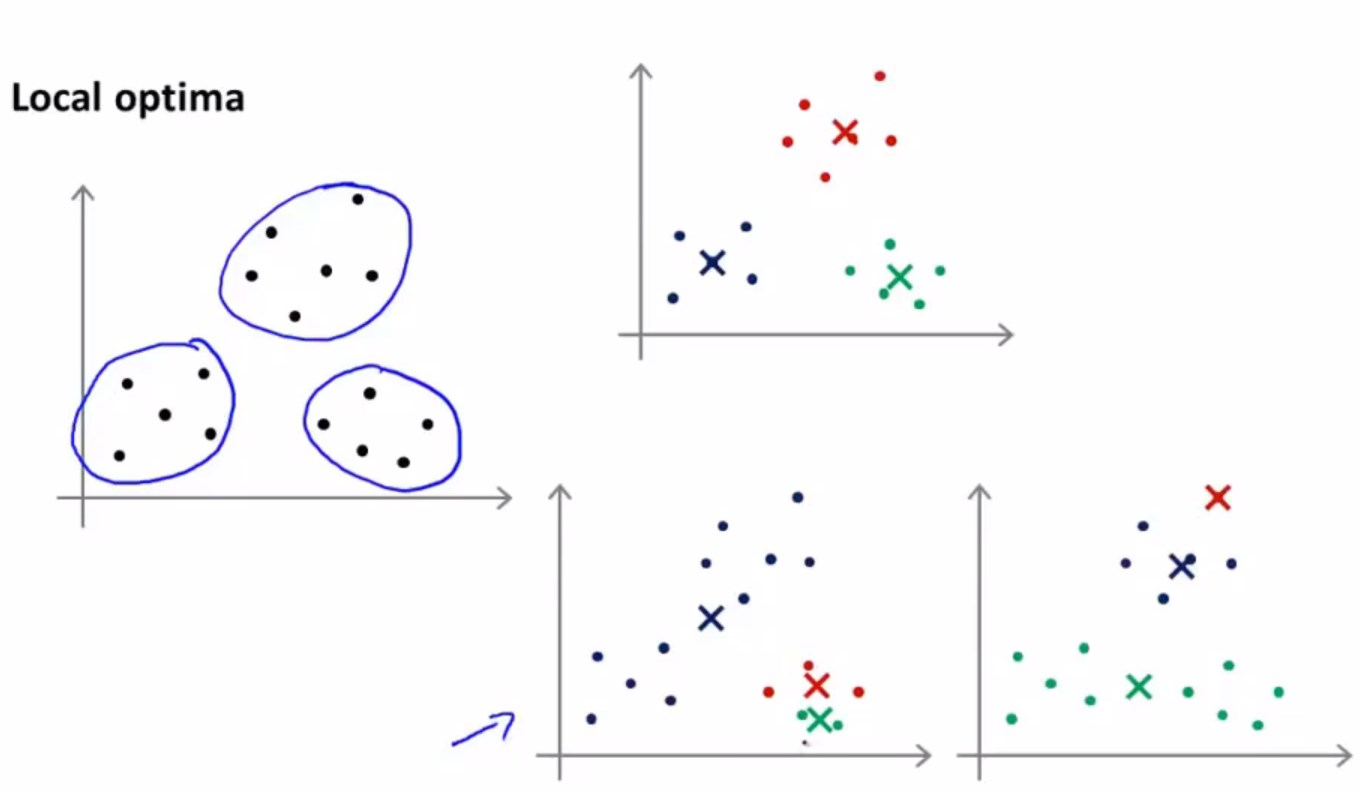
右上角的聚类结果,显而易见应该是最好的,是一个全局最优解或者说更好的局部最优解。
而右下角的两个结果,只能算是局部最优解,而且能够明显看出来,其聚类结果并不是最好的,
考虑到这是因为初始化不同而导致的不同结果,也许会想到在算法之外再嵌套一个迭代,进行多次初始化,最终选择代价函数值相对最小那个结果,经验上讲,就是全局最优解。
for i = 1 to 100(经验上来说一般是在50到1000次之间){
随机初始化聚类中心
运行K-Means算法获得\(c^1,...,c^m,\mu_1,...,\mu_K\)
计算代价函数(失真函数)\(J(c^1,...,c^m,\mu_1,...,\mu_K)\)最小值
}
最后从这100种当中选择代价最小的那一个即可。
事实证明,在运行K-Means算法时,如果用的聚类数K比较小(2-10之间),那么多次随机初始化能保证最后找到更好的聚类结果。
但是如果K特别大的话,多次随机初始化的作用就会非常小。
选择最佳的聚类数量K
聚类数量的确定没有一个明确的方法,往往是通过个人的经验与感觉去确定。通常会多尝试几次后,看哪一个选择的结果更符合实际,更符合聚类要服务的后续目的(如通过聚类进行市场分析)。
考虑这样一个例子:
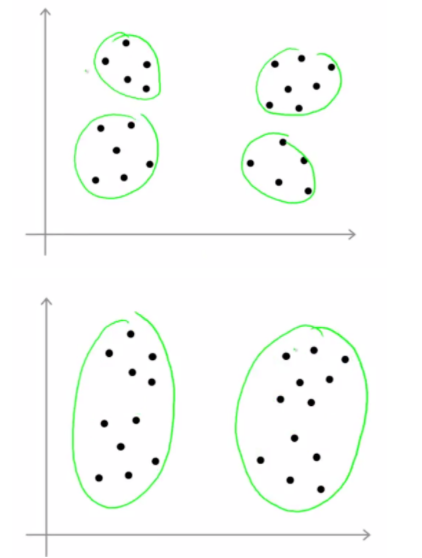
看起来两种聚类都是可行的,但是由于K的不同,最终结果出现了较大的区别。
通常情况下,可以采用一个方法,肘部法则(Elbow method)

如果通过选择不同的K值,最后得到了左边这样比较有棱有角的曲线,那么就选择位于“肘部”的那个K值就好。
但是大多数情况下,得到的是像右边那样更加模糊的一个曲线,所以肘部法则是一个值得尝试的方法,但是不具有普适性。
以T恤市场为例子:
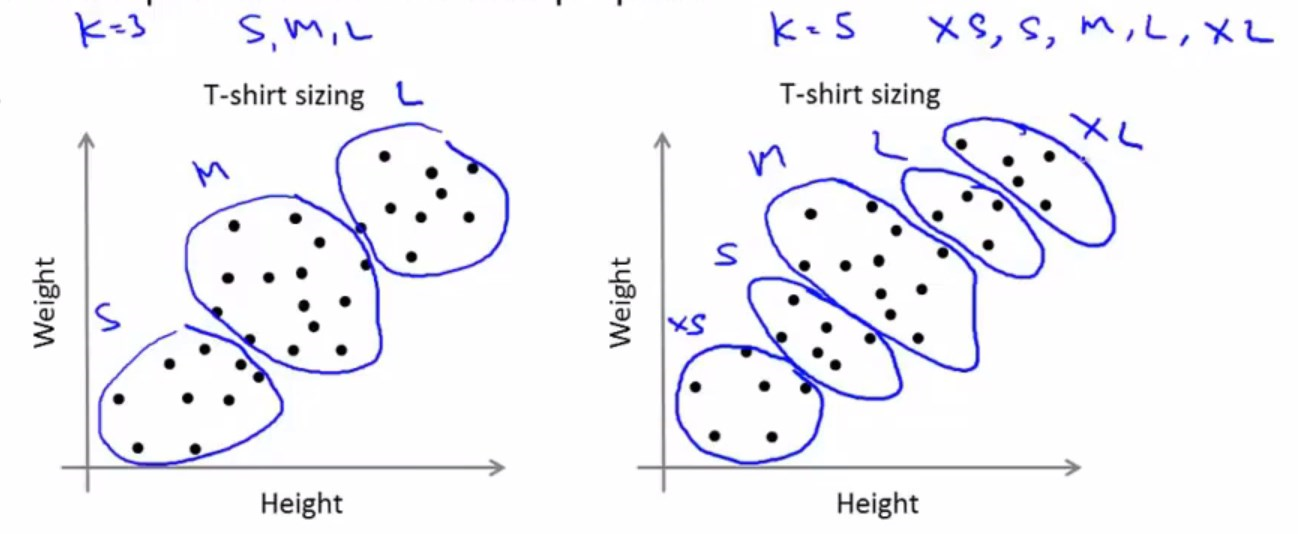
不同的K值选取,最终会聚出不同的类,考虑如果有3个尺码,和如果有5个尺码,哪个更符合市场需求,哪个更能让顾客满意,哪个更能够获取最大的利润。要考虑聚类要服务的后续目的,才能更好确定K值的选取。
轮廓系数
轮廓系数可以评判聚类好坏,通过结合簇内相似度(类内聚合度)和簇间不相似度(类间分离度)来得出。
首先给出如下定义:
\(a_i\) = 样本\(x^{i}\)与同簇内其他样本的平均距离,该值越小,说明样本\(x^i\)越应该被聚到该簇中,故可将\(a_i\)称为簇内相似度
\(b_{ij}\) = 样本\(x^{i}\)与其他簇\(C_1,...,C_K\)中所有样本的平均距离
\(b_i =min(b_{i1},...,b_{iK})\), \(b_i\)称为簇间不相似度,其值越大,说明样本\(x^i\)越不该被聚到其他任何一个簇中
那么可以给出样本\(x^i\)的轮廓系数\(s_i\)的定义:
也可以表示成:
\(s_i\)越接近1,说明样本\(x^i\)聚类越合理。
\(s_i\)越接近-1,说明样本\(x^i\)越应该聚到其他类。
\(s_i\)越接近0,说明样本\(x^i\)应该处在簇的边界上。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号