吴恩达机器学习笔记-12（支持向量机）

目录

• 支持向量机（Support Vector Machines SVM）
  • 代价函数
    • 代价函数的一些小变化
  • 假设函数
  • 大间隔分类器
    • 直观理解
    • 大间隔的数学原理
      • 内积
      • 特征与参数的内积
      • 选择大间隔的原因
  • 核函数（Kernel）
    • 核函数起作用的具体过程
    • 对于参数的选择
  • SVM的应用
    • 核函数的选择
    • 多分类问题
    • SVM与LR（logistics regression）

支持向量机（Support Vector Machines SVM）

支持向量机是一个二分类模型。比起逻辑回归和神经网络，SVM在学习某些复杂的非线性方程时能够提供一种更为清晰和更为强大的方式。

首先回顾一下之前所学过的逻辑回归的假设函数：
\(h_\theta(x)=g(z)=g(\theta^T{x})=\frac{1}{1+e^{-\theta^T{x}}}\)

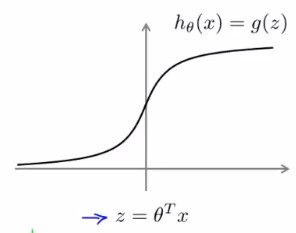
有样本y=1，为了将样本正确地分类我们会希望\(h_\theta(x)≈1\)，此时\(\theta^T{x}>>0\)
有样本y=0，为了将样本正确地分类我们会希望\(h_\theta(x)≈0\)，此时\(\theta^T{x}<<0\)

考虑之前学习逻辑回归时新令的Cost函数：

\[Cost(h_\theta{(x)},y)=-(y{\log}h_\theta{(x)}+(1-y)\log(1-h_\theta{(x)})) \]

将\(h_\theta{(x)}=\frac{1}{1+e^{-\theta^T{x}}}\)代进去，有：

\[Cost(h_\theta{(x)},y)=-y\log\frac{1}{1+e^{-\theta^T{x}}}-(1-y)\log(1-\frac{1}{1+e^{-\theta^T{x}}}) \]

代价函数

现在考虑两种情况，给出支持向量机的代价函数。

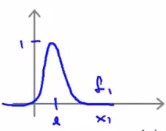
1. y=1（\(z=\theta^T{x}>>0\)）时：
   
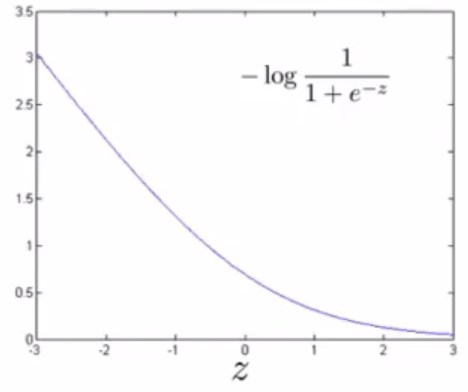
   （这是图片中函数的图像）

对这个函数图像做少量修改。

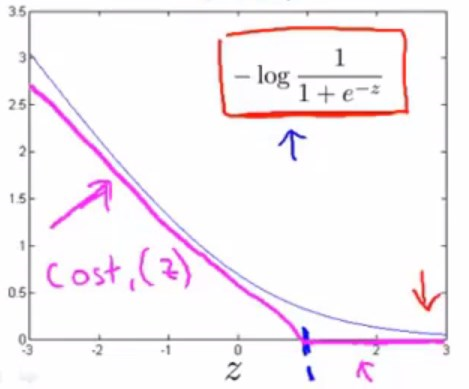
（紫色的是一个分段函数，两段均为直线，左边段的斜率不必在意，并不重要）
能看出来新的代价函数，和原有的代价函数，其实是近似的。
令这一部分紫色的函数为\(Cost_1(z)\)

1. y=0（\(z=\theta^T{x}<<0\)）时：
   
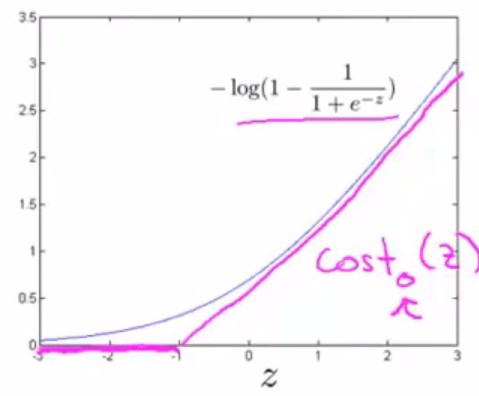
   作同样的处理。
   令这一部分紫色的函数为\(Cost_0(z)\)

代价函数的一些小变化

那么就可以初步得到SVM的最小化目标或者说代价函数为：

\[J(θ)=[\sum^{m}_{i=1}{y^i}Cost_1(\theta^T{x^i})+(1-y^i)Cost_0(\theta^T{x^i})]+\frac{\lambda}{2}\sum^n_{i=0}\theta_j^2 \]

看起来好像不太一样，因为去掉了常数\(\frac{1}{m}\)。这是因为在使用SVM时，遵循的惯例和逻辑回归有些不太一样。
去掉常数\(\frac{1}{m}\)，也并不影响求使函数最小的参数\(\theta\)。比如：\(10{(u-5)}^2+10\)，常数10并不会影响，当u=5时使得函数最小，这一结果。

我们对这个函数做如下指代：

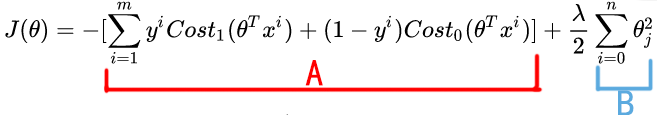
即有\(J(\theta)=A+\lambda{B}\)。欲求该式子的最小值，首先考虑的应该是选择正则化参数\(\lambda\)，以便能够权衡到底是最小化A，还是保持\(\lambda\)比较小（即更多注重B项）
按照惯例，对于SVM，我们会选择一个不同的参数，\(J(\theta)=CA+B\)，这个式子和之前的那个式子作用的等价的，因为仍然相当于是通过控制AB的权重，去求得函数最小值。

最终得到SVM的一个最小化目标或者说代价函数为：

\[J(θ)=C[\sum^{m}_{i=1}{y^i}Cost_1(\theta^T{x^i})+(1-y^i)Cost_0(\theta^T{x^i})]+\frac{1}{2}\sum^n_{i=0}\theta_j^2 \]

假设函数

SVM的假设函数并不会输出一个概率，而是输出1或0，进行的是一个更为直接的预测：

\[h_\theta(x)=\begin{cases} 1 &若\theta^x\ge0 \\\\0& 其他\end{cases} \]

大间隔分类器

SVM的目的是最大化分类间隔，间隔是指分离决策边界与离之最近的训练样本点之间的距离。

直观理解

首先回顾SVM的代价函数及其函数图像：

\[J(θ)=C[\sum^{m}_{i=1}{y^i}Cost_1(\theta^T{x^i})+(1-y^i)Cost_0(\theta^T{x^i})]+\frac{1}{2}\sum^n_{i=0}\theta_j^2 \]

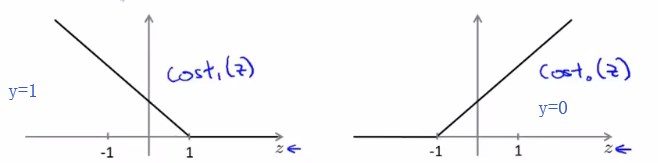
在SVM中，如果样本标签y=1，为了正确分类，我们希望\(\theta^Tx\ge{1}\)（在逻辑回归中只需要\(\ge0\)）。
在SVM中，如果样本标签y=0，为了正确分类，我们希望\(\theta^Tx\leq{-1}\)（在逻辑回归中只需要\(\lt0\)）。
与逻辑回归的这个区别，给SVM制造了一个安全因子或者安全间距。
为了更好地理解这个所谓安全间距，我们先假设一个较大的C值，C=100000。

当C非常大的时候，为了最小化代价函数，我们会希望能使\([\sum^{m}_{i=1}{y^i}Cost_1(\theta^T{x^i})+(1-y^i)Cost_0(\theta^T{x^i})]\)尽可能地趋近于0

若样本标签\(y^i=1\)，欲使\(Cost_1(\theta^T{x^i})=0\)，只需要使\(\theta^T{x^i}\ge1\)
若样本标签\(y^i=0\)，欲使\(Cost_0(\theta^T{x^i})=0\)，只需要使\(\theta^T{x^i}\le{-1}\)

那么最小化目标可以改写为：\(C\times0+\frac{1}{2}\sum^n_{i=1}\theta_j^2\)
当满足以下条件时上式成立

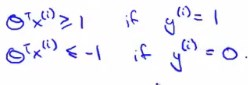
这样可以得到一个非常有趣的决策边界（图中黑线）

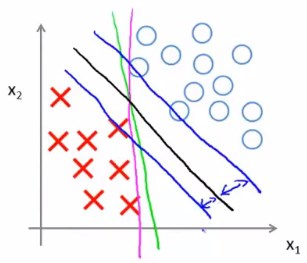
SVM的决策边界比起紫线和绿线，距离正负样本的间距更大，这个间距称为SVM的间距。
这使得SVM具有鲁棒性，在分类的时候SVM会尽量用大的间距去分离样本。
因此SVM又称为大间距分类器。

现在考虑另外一个数据集

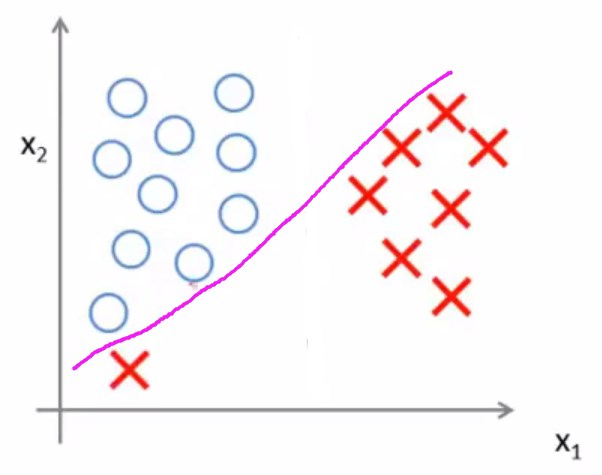
如果C非常大的话，那么SVM会对离群值（异常值）非常敏感，因为SVM总是尝试用大间距把样本分开，最终会导致得出的决策边界不具有较强的泛化性。

如果C比较小，那么会容易得出正常的决策边界

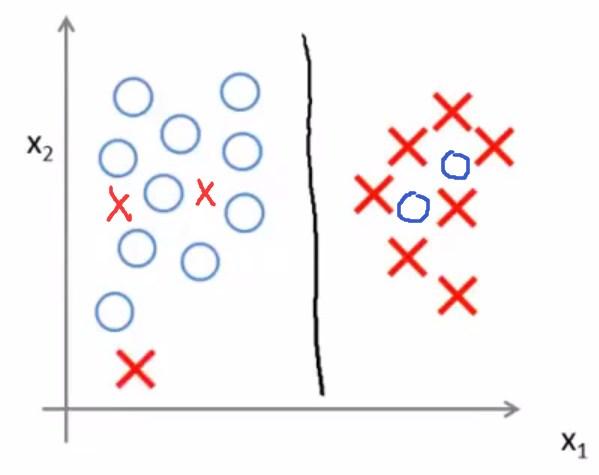
即使样本并不是线性可分的，SVM依然可以做得很好。
这里的参数\(C\)，其实起到的就是正则化的作用。

大间隔的数学原理

内积

温习一下线性代数中向量的内积。

假设有这样两个向量：
\(u=\begin{bmatrix}u_1\\\\u_2\end{bmatrix}\)\(v=\begin{bmatrix}v_1\\\\v_2\end{bmatrix}\)
该二向量的内积表示为：\(u^Tv\)

将u表示在坐标系中：

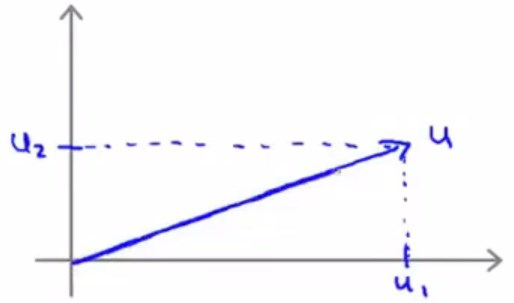
引入向量u的范数，其范数的几何意义就是向量u的长度，根据上图，容易由勾股定理得出\(||u||=\sqrt{u_1^2+u_2^2}\)

再将向量v表示在同一个坐标系中：

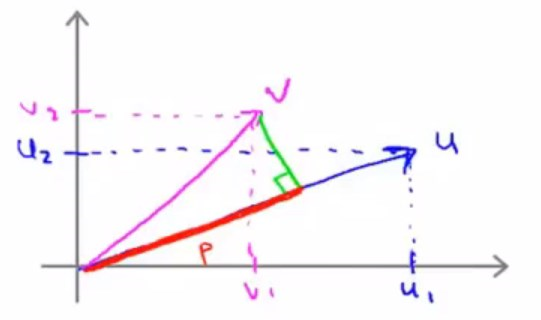
取向量v在向量u上的投影，也就是红色线段部分（定义变量p为v在u上投影的长度或者值）。

此时给出内积的定义为：\(u^Tv=p\cdot{||u||}\)
其实根据矩阵运算法则，也就是\(u^Tv=p\cdot{||u||}=u_1{v_1}+u_2{v_2}=v^Tu\)
需要注意的是p是一个实数，是有符号的，可正可负。

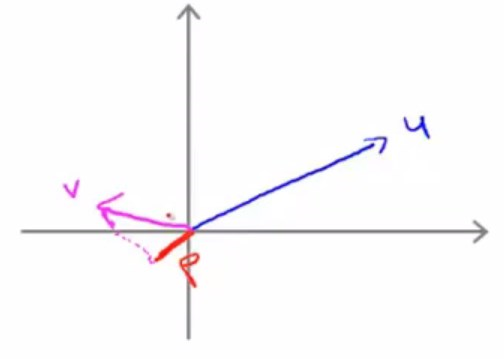
这种情况下，p就是负的。

特征与参数的内积

为了便于理解，做一个简化，令\(\theta_0=0\)，根据之前所学，\(\theta_0=0\)会使线性决策边界经过原点。
再令n=2，也就是特征数为2，这样一来就只有两个特征值\(x_1^i和x_2^i\)。
那么SVM的代价函数可以表示为\(\frac{1}{2}{(\theta_1^2+\theta_2^2)}\)
当满足以下条件时上式成立

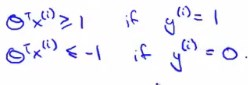
容易发现\(\frac{1}{2}{(\theta_1^2+\theta_2^2)}=\frac{1}{2}{(\sqrt{\theta_1^2+\theta_2^2})}^2\)
根据前面对于范数的定义，就能得出\(\sqrt{\theta_1^2+\theta_2^2}=||\theta||\)（\(\theta_0=0\)，所以这里可以不写出来）
那么代价函数其实就是\(\frac{1}{2}{||\theta||}^2\)

考虑一个单一的样本，即数据集中只有一个样本，该样本具有特征向量\(x=\begin{bmatrix}x_1\\\\x_2\end{bmatrix}\)
将特征向量和参数向量表示在同一坐标系中：

再根据内积的定义，那么可以得出\(\theta^Tx^{(i)}=p^{(i)}\cdot{||\theta||}=\theta_1x_1^{(i)}+\theta_2x_2^{(i)}\)

选择大间隔的原因

首先需要明确一个结论，参数向量\(\theta\)是与决策边界正交的。
因为决策边界其实就是假设函数模型在坐标系上面的表示，以上一小节的参数向量为例。
有决策边界\(\theta_1{x_1}+\theta_2{x_2}=0\)，那么决策边界的斜率就应该是\(k_1=-\frac{\theta_1}{\theta_2}\)，而参数向量\(\theta\)画出来后的斜率应该是\(k_2=\frac{\theta_2}{\theta_1}\)，显然\(k_1\times{k_2}=-1\)，所以参数向量和决策边界是正交的。

为了便于理解，还是沿用上一节的例子：

画出坐标系：

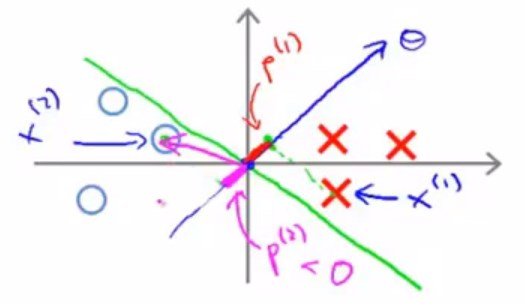
考虑如图中绿线所示的一个决策边界以及如图中这样一个数据集。
红色和紫色分别表示两个样本的特征向量在参数向量上的投影，可以看出来其值并不大。
对于正样本来说，由前面\(p^{(i)}\cdot{||\theta||}\ge1\)可以知道，较小的\(p^{(i)}\)，将会导致较大\(||\theta||\)。
类似地，对于负样本来说，由前面\(p^{(i)}\cdot{||\theta||}\leq{-1}\)可以知道，较小的\(p^{(i)}\)，同样将会导致较大\(||\theta||\)。
但是对于代价函数\(\frac{1}{2}{||\theta||}^2\)而言，要求其最小值，就是试图找到一组参数\(\theta_j\)使其向量的范数最小，产生了矛盾，所以这样一个决策边界，是不合适的。

下面考虑这样一个决策边界

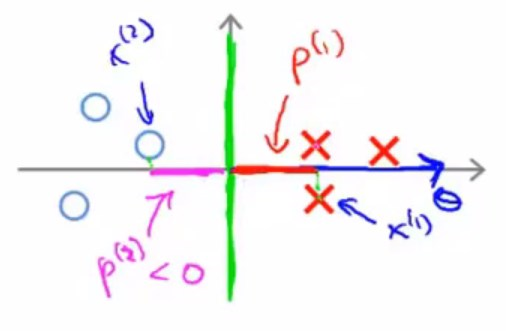
可以看出来\(p^i\)的值变大了，那么相应地\(||\theta||\)会变得更小，这就是为什么SVM总是会选择大间隔，为什么SVM也被称为大间隔分类器。另外，所谓间隔的值，其实就是\(p^i\)的值。

以上结论是可以推广到\(\theta_0\neq0\)的情况下的。

核函数（Kernel）

为了使支持向量机能够应用在复杂的非线性分类上面，需要引入核函数这个概念。

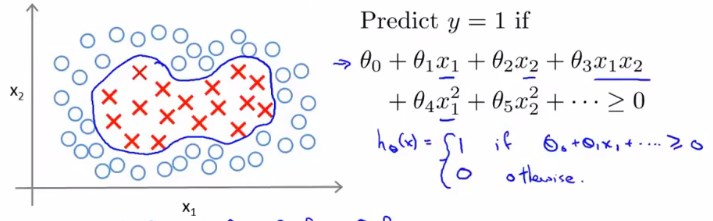
以上图为例。
考虑到实际问题中特征的复杂程度，我们需要思考能否找到更好的特征。
那么我们引入新的特征\(f_i\)来指代x。
即，\(\theta_0+\theta_1{f_1}+\theta_2{f_2}+......\)，其中\(f_1=x_1，f_2=x_2，f_3=x_1{x_2}，f_4={x_1}^2，f_5={x_2}^2，....\)
用这些f来指代原有的高次项，构造出了新的特征。
现在就需要知道，这些f具体指的是什么。

我们先人为地指定出三个点\(l^1，l^2，l^3\)（或者说三个核）。

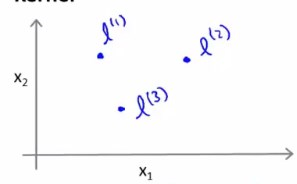
对于给定的x，我们令\(f_1=similarity(x,l^1)=e^{-\frac{{||x-l^1||}^2}{2\sigma^2}}\)（这个指数函数，其实就是高斯核函数）
（similarity指的是两个向量的相似度，这个相似度度量有很多种，核函数是其中一种。）

\(f_2=similarity(x,l^2)=e^{-\frac{{||x-l^2||}^2}{2\sigma^2}}\)
\(f_3=similarity(x,l^3)=e^{-\frac{{||x-l^3||}^2}{2\sigma^2}}\)

下面具体看下核函数做了什么。
对于\(f_1=similarity(x,l^1)=e^{-\frac{{||x-l^1||}^2}{2\sigma^2}}=e^{-\frac{\sum^n_{j=1}{(x_j-l_j^1)}^2}{2\sigma^2}}\)而言
如果\(x\approx{l^1}\)，即两者距离很近，那么\(f_1{\approx}1\)
如果\(x>>{l^1}\quad{or}\quad {x<<{l^1}}\)，即两者距离很远，那么\(f_1{\approx}0\)
在上面那个坐标系当中，新指定了三个标记点（核），每个标记点可以新定义一个特征

下面直观地来看看\(\sigma\)的一个作用：

（\(x_1，x_2\)表示的是向量x的两个元素。）

假设已经通过最小化代价函数求出了参数\(\theta\)们。

假设有这样一个x，距离\(l^1\)很近，距离\(l^2和l^3\)很远，那么\(f_1\approx1，f_2\approx0，f_3\approx0\)，最后\(\theta_0+\theta_1{f_1}+\theta_2{f_2}+\theta_3{f_3}{\approx}0.5\ge0\)
所以对于这个x，我们预测y=1。

样本多了之后，就可以看出来这个模型的决策边界是一个比较复杂的非线性函数。

核函数起作用的具体过程

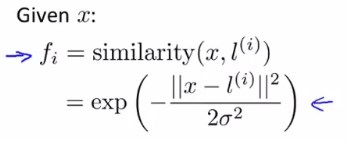
既然要靠标记点\(l^i\)来发挥核函数的作用，那么就涉及到一个如何选取标记点的问题。

一般情况下，我们会选择样本所在的位置作为标记点，这样会得到m个标记点

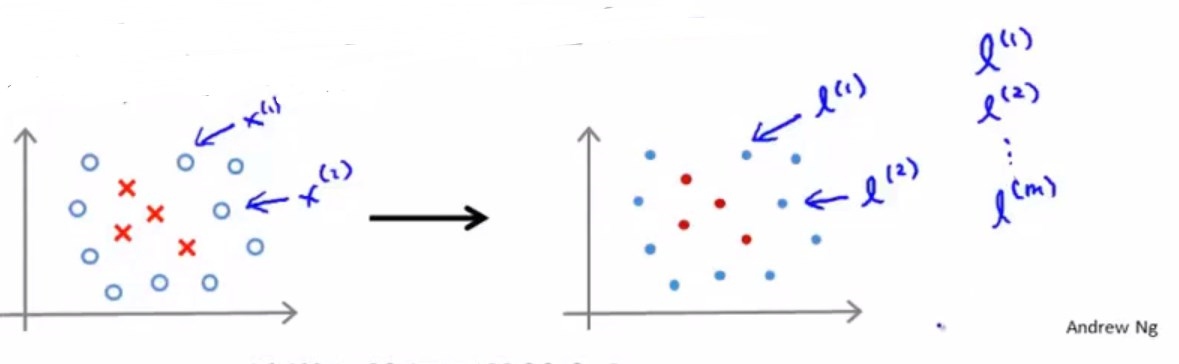
这种选取方式比较好，因为说明SVM的特征函数其实是在描述样本和其他样本的距离。

对于给定的样本

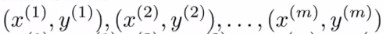
选取m个标记点

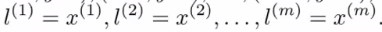
那么就有：

\[f_1^i=similarity(x^i,l^1)=e^{-\frac{{||x-l^1||}^2}{2\sigma^2}} \]

\[f_2^i=similarity(x^i,l^2) \]

\[.... \]

\[f_i^{i}=similarity(x^i,l^i)=e^{-\frac{0}{2\sigma^2}}\quad\text{衡量的是与自身的距离，所以相似度为1} \]

\[...... \]

\[f_m^i=similarity(x^i,l^m) \]

类似向量\(x^i\)，我们新令向量\(f^i=\begin{bmatrix}f_0^i\\\\f_1^i\\\\...\\\\f_m^i\end{bmatrix}\quad{f_0}^i{=1}\)，这是一个m+1维向量。
因为这是一个新特征，所以我们会在\(\theta^T{f}\ge0\)时，预测y=1。在\(\theta^T{f}\leq0\)时，预测y=0。

那么使用高斯核的SVM的代价函数需要做一些修改：

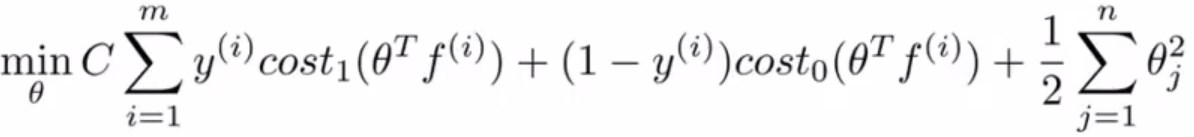
上面的n其实就等于m，因为新定义的特征f，有m个。

对于参数的选择

SVM中的参数C其实类似于参数\(\frac{1}{\lambda}\)。
因此，过大的C，会导致过拟合（低偏差，高方差）。
而过小的C，会导致欠拟合（高偏差，低方差）。

对于高斯核函数中的参数\(\sigma\)，过大的\(\sigma\)，会使特征f变化非常平缓，导致欠拟合（高偏差，低方差）。

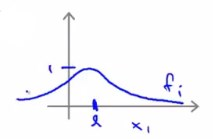
而过小的\(\sigma\)，会使特征f变化更加剧烈，导致过拟合（低偏差，高方差）。

SVM的应用

SVM有很多现成的软件包可供使用，我们只需要调用就就行，因为这些较低层的问题相对来说是比较复杂的。

核函数的选择

在应用SVM时，除了考虑参数C的选择，也要考虑核函数的选择。
一般来说，高斯核函数和线性核函数用得最多。（线性核函数就是指不使用核函数，因为不使用核函数的时候会得到一个线性的决策边界，故也称线性核函数）

当相对而言，m较小，n较大时，会更适合线性核函数（无核）。因为此时如果尝试进行复杂的非线性分类，而样本又不够，就非常容易过拟合。
当相对而言，m较大，n较小时，会更适合高斯核函数，需要选择参数\(\sigma\)
使用高斯核函数时，一些SVM包会需要程序员提供核函数的实现，也就是核函数的数学表示。在实现核函数之前，需要进行特征缩放。因为核函数计算中，分子部分等于两向量各特征差的平方和。如果特征值的尺度相差太大，将导致整个结果几乎只受值较大的特征影响。

除了线性核函数和高斯核函数，还有其他核函数可供使用，只要满足莫塞尔定理，也就是确保各种软件包，能用数值优化技巧来快速地计算出参数\(\theta\)

多分类问题

如果SVM包支持多分类问题，那么直接调用就可以了。
如果不支持，就运用（one vs all）一对多思想，将一个大类分解为多个小类，对每个小类再进行分类。

SVM与LR（logistics regression）

如果，相对而言，m很小，n很大。通常使用逻辑回归或者线性核SVM
如果，相对而言，m适中，n较小。使用高斯核SVM会比较好。
如果，相对而言，m很大，n很小。此时最好构建更多特征，然后使用LR或线性核SVM。

诚然，对于这些情况，一个设计好的神经网络都可以取得较好的效果。但是有时神经网络训练得会很慢。那么相比之下，一个封装好的SVM包，可以高效完成训练。一个好的SVM包总是会找到一个局部最优解或者其近似值。