吴恩达机器学习笔记-11(机器学习系统设计)
机器学习系统设计
常见的思想
在设计复杂的机器学习系统时可能会遇到一系列不同的问题。
以垃圾邮件分类为例子,下面会学习一些关于构建机器学习系统的知识。
假设垃圾邮件的训练集对于垃圾邮件和非垃圾邮件已经有了数字表示的标签。
即分类标签:y=1表示垃圾邮件,y=0表示非垃圾邮件。
显然这是一个监督学习问题。
为了应用监督学习算法,首先要想的是如何表示邮件的特征向量x。
在垃圾邮件分类问题中,我们会用从垃圾邮件和非垃圾邮件中选出的100个单词作为特征。

将这些单词按照字典顺序排列,下标为j(\(j=1,2,...,100\))
然后将\(x_1,x_2,...,x_j\)组合成为一个向量,就得到了特征向量x。
一般在实际工作中,在训练集中会选择出现频率最高的n个单词(n通常在10000到50000个之间),然后作为特征向量x。
为了降低误差,通常会采用以下方法:
- 收集更多的数据(如,采用蜜罐)
- 根据邮件路由信息构建更为复杂的特征向量(譬如,从邮件头中根据路由信息来构建特征,因为垃圾邮件通常会在这些地方有异常)
- 根据邮件体构建更为复杂的特征向量
- 设计更复杂的算法检测有意的错别字(比如英文邮件中的“m0rtgage”、“med1cine”、“w4tches”。或者中文邮件中的“浙筘”等等,有意而为的错误)
误差分析
手动地去观察在交叉验证集当中被错误分类的样本。通过查看这些错误,观察这些错误之间有什么共同的特征和规律,这样重复多次之后,就会启发应该从哪些地方进行改进。
以邮件分类为例子。
现假设在交叉验证集中有500个样本,即\(m_{CV}=500\)
算法误分类了100封邮件。
误差分析要做的就是,手动核查这100封邮件或者说100个错误,根据:
- 邮件类型
- 能帮助改进算法的线索或者特征
进行分类。
假设这些邮件中,有如下类别:
- 制药相关 12封
- 售卖假货 4封
- 盗取密码 53封
- 其他 31封
说明算法在对钓鱼邮件进行分类时表现得总是很差。
假设这些邮件中,有这样一些常见的垃圾邮件特征:
- 故意错别字(误拼写) 5封
- 异常邮件路由 16封
- 异常标点符号 32封
说明不必花太多时间去构建关于错别字或者误拼写的特征,而应该花时间去思考如何构建有关标点符号的特征。
总之,误差分析是一种手动检查算法所出现的失误的过程。
数值评估的重要性
改进学习算法的另一个技巧是,保证自己对学习算法有一个数值估计的方法。也就是说,如果在改进学习算法时,能够返回一个数值评价指标,来估计算法执行的效果,将会对改进算法很有帮助。
只需要对不同的方法都返回一个数值评价指标(如误差率),就可以简单明了地判断某方法对于改进算法是否有帮助。
不对称性分类的误差评估
以肿瘤分类为例,训练一个逻辑回归模型,y=1表示恶性肿瘤,y=0表示其他。
最终发现,用测试集进行检验后,有1%的错误率(99%会做出正确判断,99%情况都是正确的),看起来十分不错。
但是如果我们发现在测试集中只有0.5%的患者是真正患有癌症的,那么这个1%的错误率就显得不那么低了。
举个具体的例子,再看这样三行代码(并非一个机器学习算法,因为只处理y=0):

这三行代码忽略了输入值x,预测且只预测y=0的,即总是预测没有人得恶性肿瘤,那么在上面那个测试集当中验证的话,就只会有0.5%的错误率,甚至比1%更低。
我们把这种正例和负例数量形成极端对比的情况(比如上面这个例子中,只有0.5%的正例,99.5%全为负例)称作偏斜类(skewed classes)。
这种情况下,只预测某一类,会得到非常好的结果。
这两个例子结合起来,是为了说明,仅仅用分类误差或者分类精确度来作为评估度量,在实际情况下是不合适的。
查准率和召回率(precision&recall)
此时就需要引入新的概念,查准率和召回率。
假设我们正在用测试集来评估一个二分类模型。对于测试集中的样本,其实际的值会等于0或1(负类或者正类)。经学习算法预测出的值也会等于0或1(负类或正类)。
那么可以画出以下表格
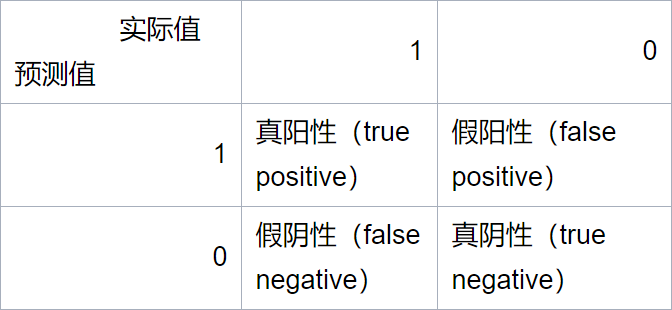
那么我们给出如下定义:
\(查准率(precision)=\frac{真阳性}{预测阳性}=\frac{真阳性}{真阳性+假阳性}\)
\(召回率(recall)=\frac{真阳性}{实际阳性}=\frac{真阳性}{真阳性+假阴性}\)
总之,对于偏斜类(skewed classes),查准率和召回率是比较好的评估度量值。
查准率和召回率的权衡
继续沿用前面的癌症分类例子,y=1表示病人患癌症,y=0表示其他。
使用之前学过的逻辑回归模型:
\(0{\leq}h_\theta(x){\leq}1\)
\(y=1\qquad if\quad{h_\theta(x)}\ge{0.5}\)
\(y=0\qquad if\quad{h_\theta(x)}\leq{0.5}\)
考虑这样的实际情况:预测病人患有癌症,会对病人的心理造成冲击,而且之后的治疗会漫长且痛苦。
出于所谓的人道主义,那么我们也许会希望只在非常确信的情况下,告诉病人患有癌症。
此时,将预测阈值调高:
\(y=1\qquad if\quad{h_\theta(x)}\ge{0.7}\)
\(y=0\qquad if\quad{h_\theta(x)}\leq{0.7}\)
这样我们会在我们确信他有\(\ge70%\)的概率情况下告诉他患有癌症,即预测y=1。
此时会有较高的查准率(因为你准备告诉的病人里面会有更大比例的人确实患有癌症,这就是为什么称为查准率 precision)和较低的召回率。
如果将阈值再调高:
\(y=1\qquad if\quad{h_\theta(x)}\ge{0.9}\)
\(y=0\qquad if\quad{h_\theta(x)}\leq{0.9}\)
这样我们会在我们确信他有\(\ge90%\)的概率情况下告诉他患有癌症,即预测y=1。
现在考虑另外一种不同的实际情况:假设我们希望避免漏掉患有癌症的人,也就是说我们希望避免假阴性。
具体地说,如果一个病人确实患有癌症,而由于学习算法的纰漏导致我们没有告诉他,或者说没有判断出他患有癌症。这显然会导致非常严重的后果,因为延误了治疗时机。
此时,理应将阈值调到一个较低的值
\(y=1\qquad if\quad{h_\theta(x)}\ge{0.3}\)
\(y=0\qquad if\quad{h_\theta(x)}\leq{0.3}\)
这样我们会在我们确信他有\(\ge30%\)的概率情况下告诉他患有癌症,即预测y=1。
宁可杀错一百也不放过一个。
这样会有较高的召回率,和较低的查准率。
可以将查准率和召回率表现到函数图像中。
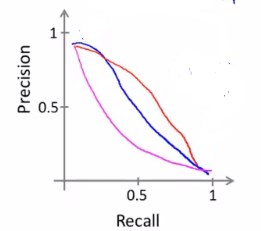
根据回归模型的不同,曲线会有一些区别。
\(F_1\)值(F值)
由于需要权衡召回率和查准率来找到回归模型的阈值,那么自然会想到,有没有办法自动选取阈值?
此时引入概念\(F_1值(F值)\),一般会直接称作F值。
假设我们有三个不同的算法,具有不同的召回率和查准率:
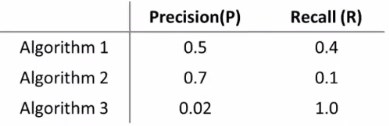
(召回率为1说明算法不管什么情况总是预测y=1)
如何权衡查准率和召回率呢?
不妨考虑取其二的平均值:\(\frac{P+R}{2}\)
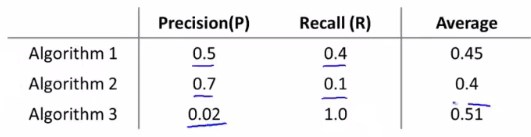
分析三个算法的查准率和召回率,能看出算法1整体比算法2更好,且其平均值比算法2的更大。那么平均值越大就是越好吗?并非如此。
且看算法3,平均值比算法1更大, 但是观察他的召回率,可以看出这是一种非常极端的情况。
以上种种说明取平均值并不是最合适的权衡P和R的方法。
此时引入\(F_1值\):\(2{\frac{PR}{P+R}}\)

观察F值的定义,会发现不管是P或者R等于0时,都会使F值为0。
当P和R的值越大时,就越能使F值变大,因此我们会选择F值最大的那个算法,或者说那些个PR值。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号