Loading

吴恩达机器学习笔记-8（正则化）

目录

过拟合问题

在学习正则化之前，我们需要先了解这样几个概念。

以线性回归为例

以房屋售价的线性回归模型为例子
image
能够看出这个假设函数并没有很好地拟合数据集，因此称之为欠拟合，也叫高偏差（bias）。

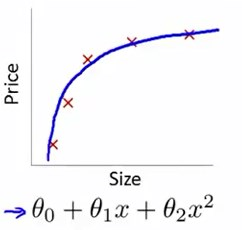
image
如果加一个二次多项式项，得出的假设函数图像能够与数据集进行较好的拟合。

倘若再极端一些，我们加入更高次的多项式项
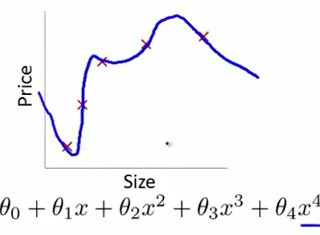
image
看起来似乎做到了最好的拟合，毕竟经过了每个训练样本，但这条线扭曲异常，上下波动，所以并不会认为这是一个预测房价的好模型。
或者说太过贴近于训练数据的特征，在训练集上表现非常优秀，近乎完美的预测/区分了所有的数据，但是在新的测试集上却表现平平。
我们称之为过度拟合、过拟合（overfitting）或者高方差（variance）。

以逻辑回归为例

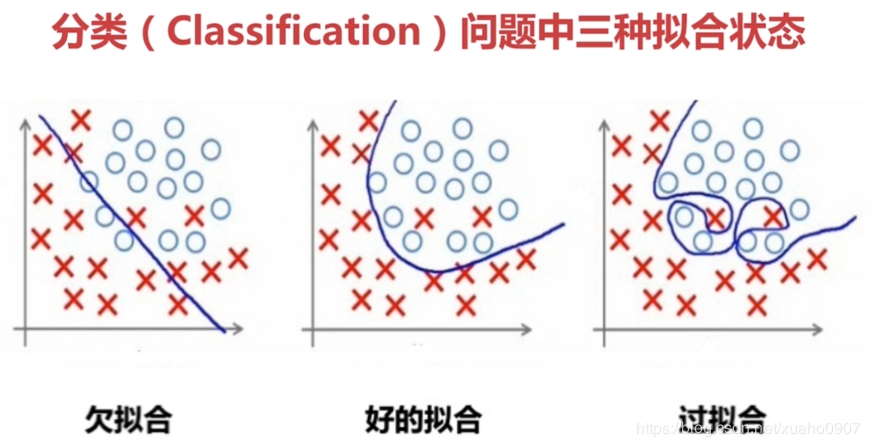
image
从左到右训练出的假设函数分别为：

  1. \(h_\theta(x)=g(\theta_0+\theta_1{x_1}+\theta_2{x_2})\)
  2. \(h_\theta(x)=g(\theta_0+\theta_1{x_1}+\theta_2{x_2}+\theta_3{x_1}^2+\theta_4{x_2}^2+\theta_5{x_1}{x_2})\)
  3. \(h_\theta(x)=g(\theta_0+\theta_1{x_1}+\theta_2{x_1}^2+\theta_3{x_1}^2{x_2}+\theta_4{x_1}^2{x_2}^2+\theta_5{x_1}^2{x_2}^2)+\theta_6{x_1}^3{x_2}+...)\)

一般来说，过度拟合会在含有太多的特征（变量）时发生，这时训练出的假设函数总能很好地拟合训练数据，代价函数值可能会很低，甚至接近0。但是无法泛化（泛化：假设模型能够应用到新样本中的能力）到新的数据样本中。

解决过拟合

有这样几个方法：

  1. 减少特征数量
    • 手动保留应当留下的特征
    • 模型选择算法
  2. 正则化
    • 保留所有特征，但是减少特征的数量级或者参数\(\theta_j\)的值
    • 正则化在很多特征变量对目标值只有很小影响的情况下非常有用。毕竟不希望舍弃掉有用的特征值。

正则化

以房屋售价的线性回归模型为例子。
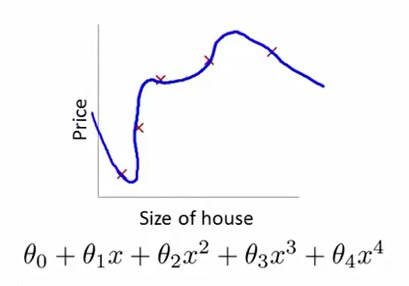
image
我们有这样一个数据集，及其假设函数。
考虑之前学的代价函数\(J(θ)=\frac{1}{m} \sum^{m}_{i=1}{\frac{1}{2}}{(h_θ(x_i)-y_i)^2}\)
我们现在修改一下代价函数，加上两个正则化项（regularizer）或惩罚项（penalize term）
\(J(θ)=\frac{1}{m} \sum^{m}_{i=1}{\frac{1}{2}}{(h_θ(x_i)-y_i)^2}+1000\theta^2_3+1000\theta_4^2\)（1000是任意指定的比较大的系数）
我们需要最小化\(J(\theta)\)的值，就要使\(\theta_3，\theta_4\)的值尽量小，接近于0。
那么假设函数就会近似为一个二次函数，过拟合也就解决了。

一般来说，如果参数\(\theta_j \qquad j=0,1,...,n\)的值比较小，我们往往可以得到一个更简单的假设函数，就不容易发生过拟合。

详解正则化

以房屋售价为例
我们有100个特征，101个参数\(\theta\)
image
我们不知道该去正则化哪个或哪些参数\(\theta\)。
所以在通常的正则化步骤中，我们会将代价函数修改如下：
\(J(θ)=\frac{1}{2m} \sum^{m}_{i=1}{(h_θ(x_i)-y_i)^2}+{\lambda\}sum^n_{j=1}\theta_j^2\)
其中\({\lambda\}sum^n_{i=1}\theta_j^2\)就是所谓的正则化项，需要注意的是，约定不对\(\theta_0\)进行正则化。
经过对最小化代价函数的过程，减少参数\(\theta_j\)的值。

再看\(J(θ)=\frac{1}{2m} \sum^{m}_{i=1}{(h_θ(x_i)-y_i)^2}+{\lambda\}sum^n_{i=1}\theta_j^2\)
参数\(\lambda\)即正则化参数，它的作用是控制\(\sum^{m}_{i=1}{(h_θ(x_i)-y_i)^2}\)与\(sum^n_{i=1}\theta_j^2\)之间的平衡关系。从而避免过度拟合。

不禁会想，如果参数\(\lambda\)的值过分大，譬如\(\lambda=10^{10}\)，会出现什么情况？
这样会使从\(\theta_1 to \theta_n\)的每个参数值最终都非常小，使得假设函数近似为\(h_\theta(x)=\theta_0\)，形成一条直线，去拟合数据集，这就造成了欠拟合。

正则化线性回归

根据前面所学，有正规化代价函数\(J(θ)=\frac{1}{2m} \sum^{m}_{i=1}{(h_θ(x_i)-y_i)^2}+{\lambda\}sum^n_{i=1}\theta_j^2\)

梯度下降

回顾之前所学，有参数更新方程如下：

\[θ_0 := θ_0 - α\frac{1}{m} \sum_{i=1}^m(h_\theta{(x^i)}-y^i)x^i_0 \qquad {\text{j=0}} \]

\[θ_j := θ_j - α\frac{1}{m} \sum_{i=1}^m(h_\theta{(x^i)}-y^i)x^i_j \qquad {\text{j=1,2,3,...,n}} \]

（因为正则化不对\(\theta_0\)操作，所以单独把\(\theta_0\)的情况拿出来）

那么引入正则化之后，将对参数更新方程作如下修改

\[θ_j := θ_j - α\frac{1}{m} \sum_{i=1}^m(h_\theta{(x^i)}-y^i)x^i_j+\frac{\lambda}{m}\theta_j \qquad {\text{j=1,2,3,...,n}} \]

（其实就是对引入了正则化后的代价函数求的偏导）

可以改写为如下形式：

\[θ_j := θ_j(1 - α\frac{\lambda}{m})-\alpha\frac{1}{m} \sum_{i=1}^m(h_\theta{(x^i)}-y^i)x^i_j \qquad {\text{j=1,2,3,...,n}} \]

可以发现\(1 - α\frac{\lambda}{m}\)是一个比1略小的数，因为\(\alpha\)通常较小而m通常较大，那么更新的结果就是将\(\theta_j\)向0的方向缩小了一点点，使得\(\theta_j\)变小了一点点，具体点说就是缩小了\(\theta_j\)的平方范数
而\(\alpha\frac{1}{m} \sum_{i=1}^m(h_\theta{(x^i)}-y^i)x^i_j\)这一部分与正则化前的更新方程是一模一样的，所以当我们进行线性回归的正则化时，就只是把\(\theta_j\)缩小一点点，然后进行同样的更新操作。

正规方程

回顾之前所学，构建m\times{n+1}$阶设计矩阵

\[X=\begin{bmatrix}{(x^{(1)})}^T\\\\...\\\\{(x^{(1)})}^T\end{bmatrix} \]

正规方程的公式为:

\[\theta=(X^TX)^{-1}X^Ty \]

引入正则化后，公式变为：
image
其中的对角阵为\({n+1}\times{n+1}\)阶

不可逆时

根据前面所学，当样本数m<特征数n时，\(X^TX\)是不可逆的。
引入正则化后，如果正则化参数\(\lambda\)严格>0，则
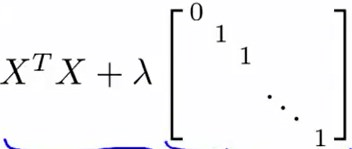
image
该项是必然可逆的。

正则化逻辑回归

类似于线性回归，我们正则化逻辑回归的代价函数如下：

\[J(θ)={-}{\frac{1}{m}}[\sum^{m}_{i=1}{y^i}\log(h_\theta{(x^i)}+(1-y^i)\log(1-h_\theta{(x^i)})]+\frac{\lambda}{2m}\sum^n_j\theta_j^2 \qquad j=1,2,...,n \]

梯度下降

类似于线性回归：

\[θ_0 := θ_0 - α\frac{1}{m} \sum_{i=1}^m(h_\theta{(x^i)}-y^i)x^i_0 \qquad {\text{j=0}} \]

\[θ_j := θ_j - α\frac{1}{m} \sum_{i=1}^m(h_\theta{(x^i)}-y^i)x^i_j+\frac{\lambda}{m}\theta_j \qquad {\text{j=1,2,3,...,n}} \]

（因为正则化不对\(\theta_0\)操作，所以单独把\(\theta_0\)的情况拿出来）
（其实就是对引入了正则化后的代价函数求的偏导
）

高级优化

image

posted @ 2021-06-09 10:49  mmmhongyu  阅读(230)  评论(0)    收藏  举报