吴恩达机器学习笔记-7(逻辑回归)
逻辑回归
前面有学到过,可以按照任务的种类,将任务分为回归任务和分类任务。
这两者的区别在于,输入变量与输出变量均为连续变量的预测问题是回归问题,输出变量为有限个离散变量的预测问题成为分类问题。
譬如,我们要预测的结果是一个数,通过房屋面积来预测房屋的售价,房屋的售价可能会有无数多种,有卖几百万的,有卖几十万的。预测结果是一个确定的数,而是哪个数则有无数种可能。这样的预测结果表现在函数图像上是连续的,所以称这类问题为回归问题。
譬如,我们要预测一个肿瘤是否为恶性肿瘤,邮件是否为垃圾邮件。这种问题的预测结果只有几个或多个有限的值。在函数图像上是离散的。我们可以将这些值归为不同的类,预测对象究竟属于哪个类,故称为分类问题。
更深一步讲,如果一个分类问题的结果只有“是”或“不是”两种可能,那么我们可以将“是”的结果称为正例,而“不是”的结果称为负例。
需要注意的是,通常或从直觉上讲,负例总是表示缺少某样东西的意思。
尝试用线性回归解决分类问题
逻辑回归,是用于分类问题的经典算法,从字面上的意思来看,也许是用回归的方法来做分类问题。
由之前所学,我们可以尝试用线性回归模型去解决分类问题。
以根据肿瘤尺寸来预测肿瘤是否恶性为例子。
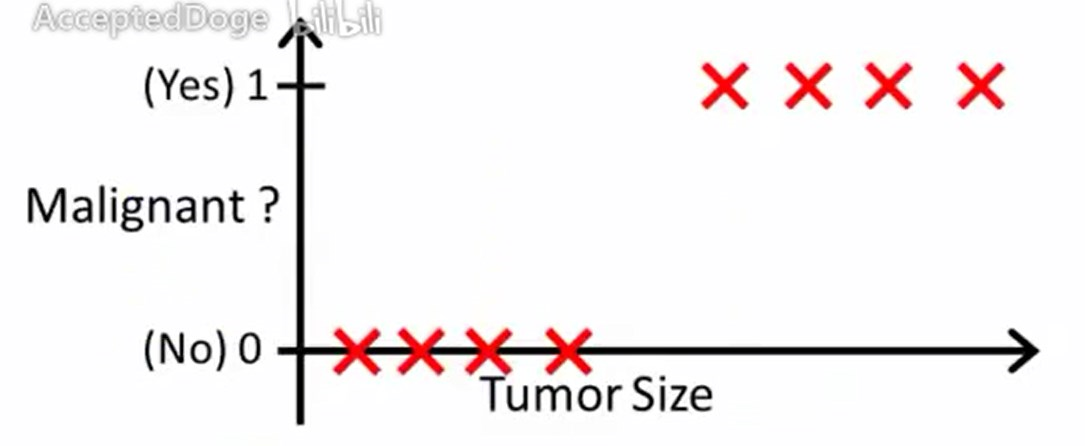
我们有这样一个训练集。
运用线性回归模型,首先要得到一个假设函数,去尽量拟合这些样本。
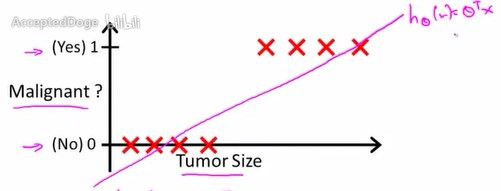
假设函数为\(h_\theta(x)=\theta^T{x}\)
我们可以将分类器输出阈值设为0.5

那么容易看出,假设函数值大于等于0.5的样本,就预测其y值为1,即恶性肿瘤。
假设函数值小于0.5,就预测y值为0,即良性肿瘤。
如此一来,通过线性回归加阈值设定,就把一个简单的二分类问题转换为了回归问题。
但是很多时候,训练集并不能简单地用线性回归模型去拟合。
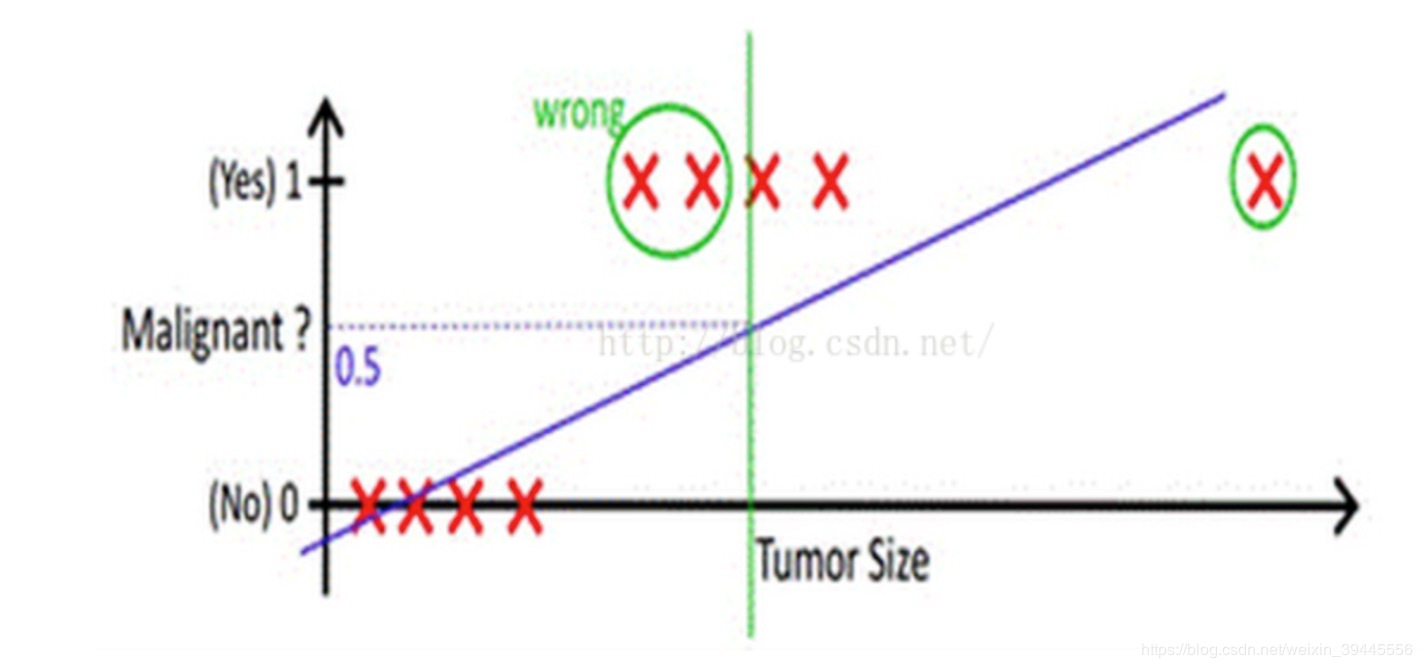
现在假设有一个超大尺寸的肿瘤在训练集中,加入我们用线性回归模型去拟合,并且阈值还是取0.5。
容易看出,有两个正例被错误的分类到负例当中。说明用线性函数去拟合并取阈值的办法行不通了。行不通的原因是函数图像过于直,容易受到训练集中的离群值(异常值)的影响。
那么我们接下来应该考虑两件事
- 用一个不那么直的函数去拟合
- 选定正确的阈值
Sigmoid函数
我们有提到,希望假设函数输出值在0到1之间,这样才能起到用回归模型去解决分类问题的作用。
那么需要引进一个统计学中非常特别的函数。
Sigmoid函数(Logistic函数):\(g(z)=\frac{1}{1+e^{-z}}\)其中z是实数。
函数图像如下:
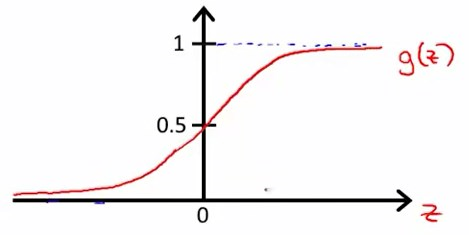
无限趋近于0,同时无限趋近于1。
可以看出,\(0\leq{g(z)}\leq1\),完全符合我们对值域的要求。考虑到z是实数,而线性回归模型中假设函数\(h_\theta(x)=\theta^T{x}\)中的\(\theta^T{x}\)也是实数,所以我们可以构建一个新的假设函数为$$h_\theta(x)=g(z)=g(\thetaT{x})=\frac{1}{1+e{-\theta^T{x}}}$$
到了这里,就又回到了回归问题,我们需要寻找一个参数\(\theta\)使得假设函数尽可能地拟合训练集。
新假设函数详解
由上面可知,新的假设函数为
统计学中,将这个假设函数值定义为,是对于新输入样本x,y=1的概率的估值。
譬如,有特征向量
此时有某患者的样本x输入,得到\(h_\theta(x)=0.7\),那么对于该患者而言y=1的概率为0.7,或者说该患者肿瘤是恶性的可能为为70%。
更加具体或者说更加符合统计学概念地表示假设函数的话,应该如下:
是一个条件概率,指的是给定参数\(\theta\),对于某个特征为x的病人,y=1的概率。
因为\(y=0 or 1\),所以\(P(y=1|x;{\theta})+P(y=0|x;{\theta})=1\),那么容易求得\(P(y=0|x;{\theta})=1-P(y=1|x;{\theta})\)
决策边界(decision boundary)
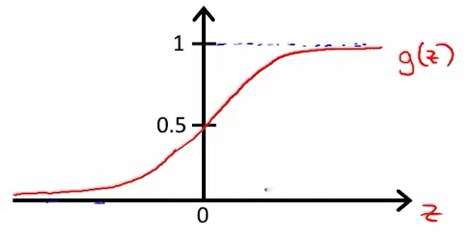
回顾Sigmoid函数图像。
我们可以看到,
当\({z}\ge0\)时,\({g(z)}\ge{0.5}\)。即当\(\theta^T{x}\ge{0}\)时,\(h_\theta(x)=g(\theta^T{x})\ge0.5\),此时预测y=1。
当\({z}\leq0\)时,\({g(z)}\ge{0.5}\)。即当\(\theta^T{x}<{0}\)时,\(h_\theta(x)=g(\theta^T{x})<0.5\),此时预测y=0。
线性决策边界
现在假设有这样一个数据集
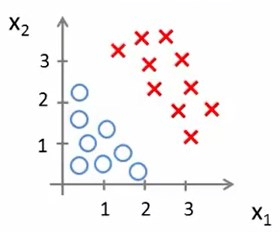
并且假设我们的假设函数是\(h_\theta(x)=g(\theta_0+\theta_1{x_1}+\theta_2{x_2})\)
假定此时已经找到了在此例中最佳的参数\(\theta_0={-3} \theta_1={1} \theta_2={1}\)
那么\(\theta=\begin{bmatrix}-3\\\\1\\\\1\end{bmatrix}\)
即\(\theta^T{x}=-3+x_1+x_2\)
根据前面所讲,当\(\theta^T{x}=-3+x_1+x_2\ge{0}\)时,预测y=1。
容易注意到\(x_1+x_2=3\)的函数图像应该如下:
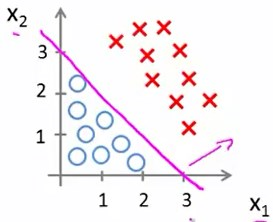
那么在此例中,这条直线上方,即\(-3+x_1+x_2\ge{0}\)时,预测y=1.
这条直线下方,即\(-3+x_1+x_2\leq{0}\)时,预测y=0.
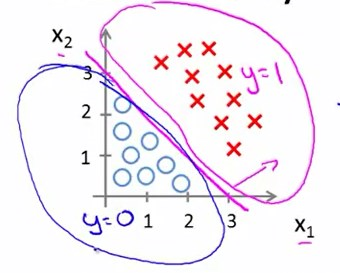
我们将这条直线称为决策边界,也就是说在这条线的两边是不同的类,不同的决策。
决策边界是假设函数的一个属性,而无关数据集。
非线性决策边界
假设我们有这样一个数据集,这显然需要非线性的函数才能最佳拟合。
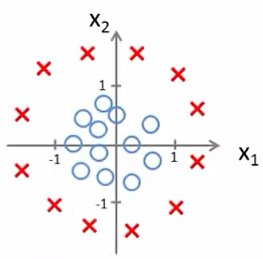
多项式回归那里有学到,可以添加额外的高次多项式项,来使函数图像发生变化
假设函数是\(h_\theta(x)=g(\theta_0+\theta_1{x_1}+\theta_2{x_2}+\theta_3{x_1^{2}}+\theta_4{x_2^{2}})\)
假定此时已经找到了在此例中最佳的参数\(\theta_0={-1} \theta_1={0} \theta_2={0} \theta_3={1} \theta_4={1}\)
那么\(\theta=\begin{bmatrix} -1\\\\0\\\\0\\\\1\\\\1 \end{bmatrix}\)
即\(\theta^T{x}=-1+x_1^2+x_2^2\)
根据前面所讲,当\(\theta^T{x}=-1+x_1^2+x_2^2\ge{0}\)时,预测y=1。
容易注意到\(-1+x_1^2+x_2^2=0\)的函数图像应该如下:
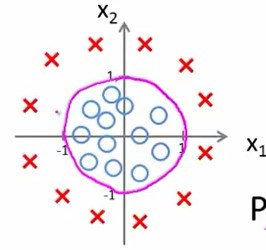
那么在此例中,这个圆外部,即\(-1+x_1^2+x_2^2\ge{0}\)时,预测y=1.
这个圆内部,即\(-1+x_1^2+x_2^2\leq{0}\)时,预测y=0.
同理,我们可以用更复杂的模型生成复杂的决策边界去拟合更为复杂的数据集。
代价函数
之前推导线性回归模型时,我们用到了这样的代价函数\(J(θ)=\frac{1}{m} \sum^{m}_{i=1}{\frac{1}{2}}{(h_θ(x_i)-y_i)^2}\)
为了便于理解逻辑回归的代价函数,我们新令Cost函数\(Cost(h_\theta{x},y)={\frac{1}{2}}{(h_θ(x)-y)^2}\),也就是说\(J(θ)=\frac{1}{m} \sum^{m}_{i=1}Cost(h_\theta{(x)},y)\)
下面是逻辑回归的Cost函数
容易作出y在两种情况下的函数图像:
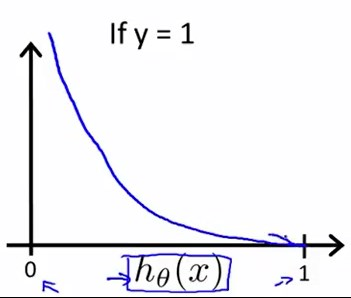
当y=1时,且\(h_\theta{(x)}=1\),此时\(Cost=0\)
当y=1时,且\(h_\theta{(x)}→0\),此时\(Cost→\infty\)
具体点,可以这样理解,倘若病人患有恶性肿瘤,而学习算法预测出并非恶性肿瘤,那么我们就要严厉地惩罚学习算法,学习算法就会付出很大很大的代价。
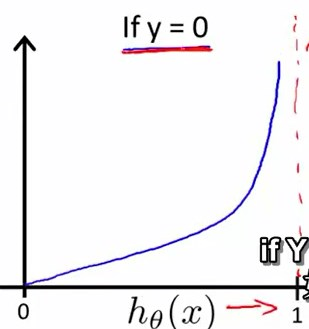
当y=0时,且\(h_\theta{(x)}=0\),此时Cost=0
当y=0时,且\(h_\theta{(x)}→1\),此时\(Cost→\infty\)
同理,也很好理解,不再赘述。
简化代价函数
为了便于利用梯度下降算法来求出参数\(\theta\),我们需要将\(Cost(h_\theta{(x)},y)=\begin{cases} -\log(h_\theta{(x)}& \text{if y=1}\\\\-\log(1-h_\theta{(x)}) &\text{if y=0} \end{cases}\)简化为一行,如下:
显然简化后的函数在\(y=0 or 1\)的情况下与简化前的分段函数是完全等价的。
那么终于可以得出完整的逻辑回归代价函数如下:
逻辑回归的梯度下降
逻辑回归的假设函数为\(h_\theta(x)=g(z)=g(\theta^T{x})=\frac{1}{1+e^{-\theta^T{x}}}=P(y=1|x;{\theta})\),其值为一个概率。
根据之前学过的梯度下降,我们容易得到梯度下降模板如下:
其中\(\frac{∂J(θ)}{∂θ_j}=\frac{1}{m} \sum_{i=1}^m(h_\theta{(x^i)}-y^i)x^i_j \qquad {\text{j=0,1,2,3,...,n}}\)
\(\theta\)可以表示为\(\theta=\begin{bmatrix}\theta_0\\\\{\theta_1}\\\\{\theta_2}\\\\...\\\\{\theta_n}\end{bmatrix}\)
我们发现求导之后的式子和线性回归中的那个式子一模一样,但由于假设函数的不同,两者其实是完全不同的。
优化
除了用梯度下降算法计算参数\(\theta\),还有其他更为高效的算法:
- 共轭梯度法
- BFGS(变尺度法)
- L-BFGS(限制变尺度法)
这三个算法有共同的特点:
|优点|缺点|
|---|---|
|无需手动选择\(\alpha\)|更为复杂|
|通常比梯度下降快得多|---|
由于过于复杂,所以我们可以不必理解清楚这些算法实现的细节,而仅仅只需要掌握其用法。
假设我们有这样一个问题:
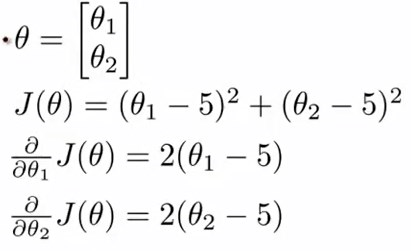
在Octave\matlab中的代码如下:

因为有两个需要计算的偏导,所以用一个\(2\times{1}\)的向量来存储值。
gradient(1)是关于\(\theta_0\)的偏导数的值,因为octave\matlab的下标是从1开始,后面的以此类推。
接着调用内置优化函数fminunc

调用这个函数需要配置options,在options中‘GradObj’表示梯度目标参数。‘on’表示设置梯度目标参数为打开,默认情况下是关闭的。‘MaxIter’表示优化结束前的最大迭代次数。‘100’表示最大迭代次数为100次。
第二行initialTheta表示给出一个参数\(\theta\)的初始猜测值。
第四行中的‘@’符号表示指向costFunction函数的指针。
多类别分类问题(Multiclass Classification)
所谓多类别分类问题,如,将邮件归档到工作、朋友、家人、爱好不同的文件夹中,这样就有了4个类别,我们分别用y=1、y=2、y=3、y=4来表示。
再如有患者因为鼻塞就医,他的诊断结果可能有如下3中类别:没病(y=1)、感冒(y=2)、流感(y=3)。
再如天气分类问题,晴天(y=1)、多云(y=2)、雨(y=3)、雪(y=4)。
以上都是多类别分类问题,y的值可以任意指定,不必纠结。
前面谈到的肿瘤预测问题,其实是一个二分类问题
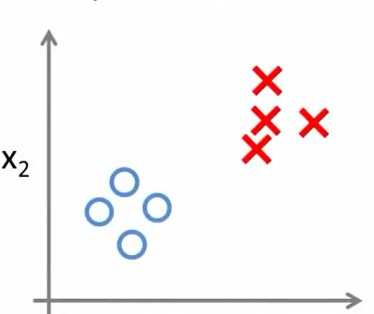
显然,多类别分类问题应当如此表示:
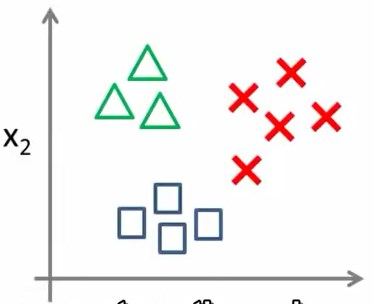
一对多(一对余)思想(one-vs-all or one-vs-rest)
我们将上面的三分类问题,处理为多个二分类问题。
我们需要创建一个新的训练集
我们将方形和叉形的样本看作一类,三角形看作另一类
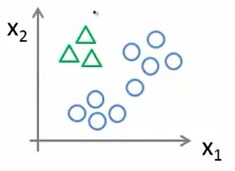
我们把圆形设为负例(negative),三角形设为正例(positive),那么由前面所学,圆形的值应为0,三角形的值应为1,这样就得到一个决策边界
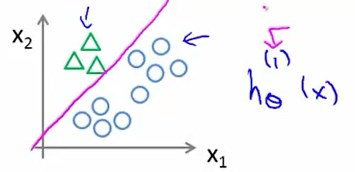
假设函数\(h_{\theta}(x)^{(1)}\)中的1表示类别1。
同理有类别2
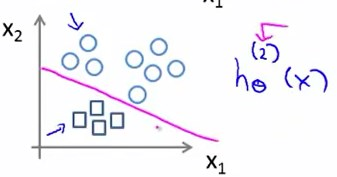
方块为正例,圆形为负例。
类别3
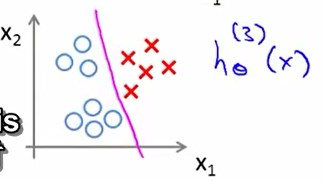
叉形为正例,圆形为负例。
那么相应地,假设函数应改为\(h_\theta^{(i)}(x)=P(y=i|x;{\theta})\qquad(i=1,2,3)\)
将欲预测样本分别输入三个分类器中,取预测值最大的那个分类器。因为前面有讲到预测值\(h_\theta(x)\)是概率,如果预测值最大,说明该分类器是可信度最高,效果最好的那个。那么就可以完成一次分类,两次分类之后就可以解决该三分类问题。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号