吴恩达机器学习笔记-2(一元线性回归)
单元线性回归模型
当您要根据单个输入值x预测单个输出值y时,使用单变量线性回归。 我们在这里进行有监督的学习,因此这意味着我们已经对输入/输出因果关系应该有所了解。
在监督学习中,我们有一个数据集,这个数据集被称为训练集。
以住房价格为例:
算法的任务是从这个数据集(训练集)中学习如何预测房价
| 面积(x) | 单价(y) |
|---|---|
| 2104 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
| …… | …… |
| **\(m\):训练样本数,在表格中表现为行数 | |
| \(x\):输入变量/特征 | |
| \(y\):输出变量/要预测的目标变量 | |
| \((x,y)\):表示一个训练样本 | |
| \((x^i,y^i)\):表示特定的训练样本,i表示第几行,如\(x^1 = 2104\)** |
监督学习的目标是,给定一个训练集,去生成(学习)一个函数h,这个函数h(x)是对应于y值的“好”预测函数,这个函数按照惯例被称为假设函数(hypothesis)
流程图如下:
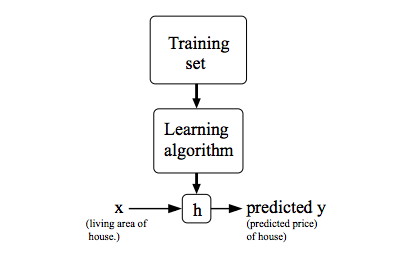
- 向学习算法中输入训练集,得到预测函数h。
- 向预测函数h中输入变量x,得到变量y
当我们试图预测的目标变量(y)是连续的,则称这个问题为回归问题。
当y只能取少量的离散值时(例如,若给定房屋面积,我们想预测一房屋是别墅还是公寓),则称之为分类问题
在设计学习算法时,我们需要考虑的一个问题是,如何表示预测函数h?
我们以如下方式表示:
\(\theta_i\):模型参数
要做的就是如何选择模型参数,使得预测函数更加拟合训练集中的样本
下图说明了不同取值对函数图像的影响
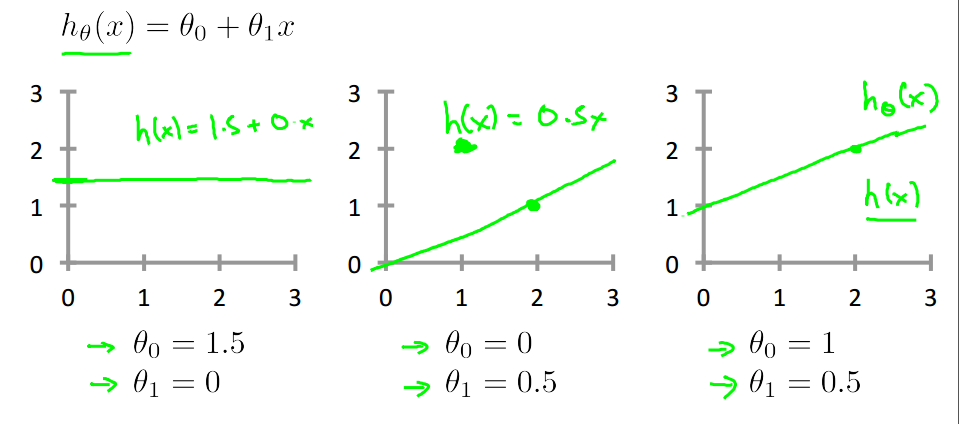
在线性回归中,我们有一个数据集,如下图:
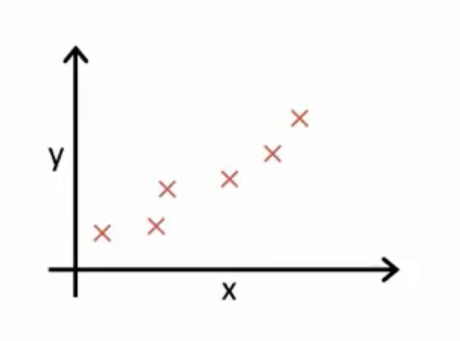
我们要做的就是得出\(θ_0\) \(θ_1\)的值,使得预测函数h表示的直线尽可能地拟合这些个样本
前面提到了训练集中有x和y,x是输入的特征,y是要预测的目标值。
既然要求尽可能拟合,那么我们就需要选择合适的\(θ_0\) \(θ_1\)使得h(x)和y的差值最小
因为有m个样本,所以要对这个差值求和,那么有:
\(h_θ(x_i)\):预测函数h的值
\(y_i\):训练集中给出的实际值
\((x_i,y_i)\):表示特定的训练样本
乘\(\frac{1}{m}\)是为了避免样本数量对值的影响
此函数\(J(θ_0,θ_1)\)称为“平方误差函数”或“均方误差”。为了便于计算梯度下降,平均值减半(乘\(\frac{1}{2}\)),因为平方函数的导数项将抵消\(\frac{1}{2}\)项,便于求导
此时就把问题变成了,找到能使预测值和真实值的差值的平方的和最小,的\(θ_0,θ_1\)的值
令\(θ_0 = 0\)的特殊情况
为了更好地理解代价函数
我们将预测函数h简化为
即令\(θ_0 = 0\),相当于预测函数必定经过原点
如下图:
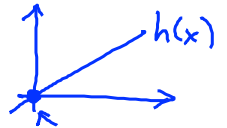
那么代价函数变为:
即求此函数的最小值
对于给定的\(θ_1\),函数h是一个关于x的函数
相比之下,代价函数J是一个关于\(θ_1\)的函数
先假定\(θ_1=1\)
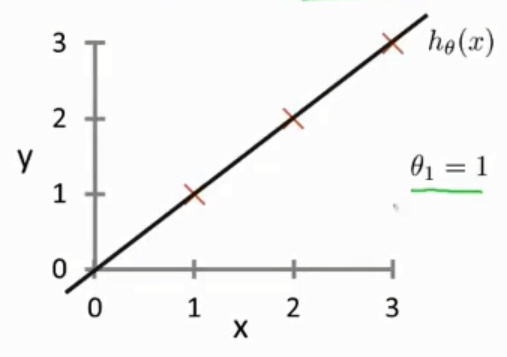
那么此时\(h(x_1) = 1, h(x_2) = 2, h(x_3) = 3\)
又根据样本,\(y_1 = 1, y_2 = 2, y_3 = 3\)
根据代价函数的表达式,容易得出
再假定\(θ_1=0.5\)

那么此时\(h(x_1) = 0.5, h(x_2) = 1, h(x_3) = 1.5\)
又根据样本,\(y_1 = 1, y_2 = 2, y_3 = 3\)
根据代价函数的表达式,容易得出
当经过一系列的取值计算后,可以得出代价函数J的图像是符合其表达式的一个二次函数
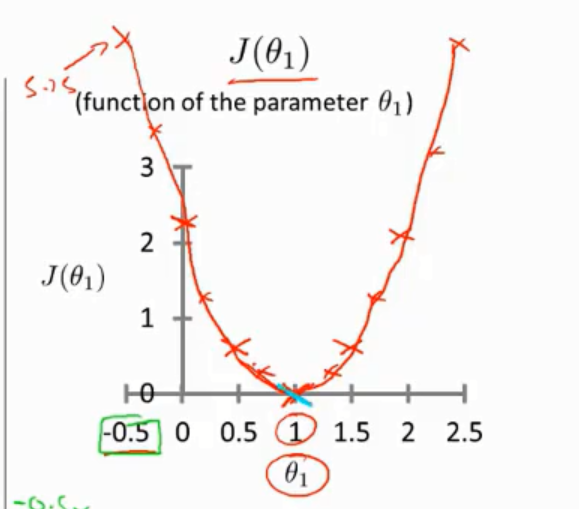
那么在这个例子中,\(θ_1 = 1\)是我们要求的全局最小值
线性回归模型中的一般情况
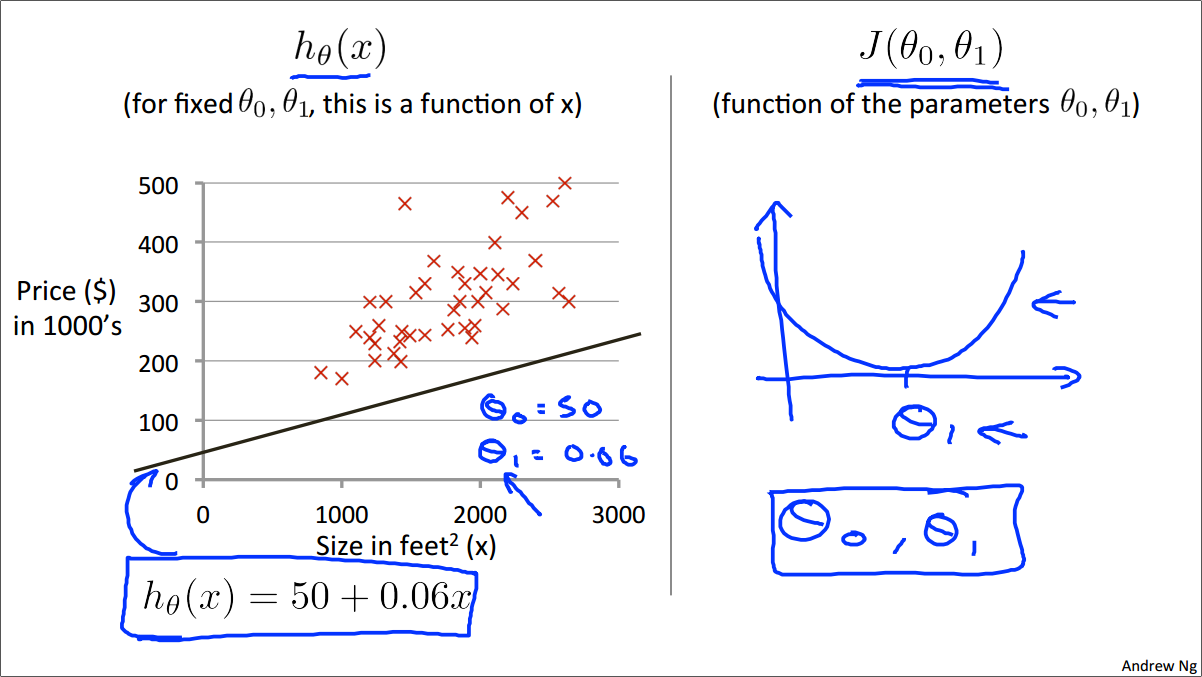
在这个例子中,\(θ_0 = 50, θ_1 = 0.06\)
预测函数h为
\(h_θ(x) = 50 + 0.06x\)
此时得到的代价函数图像应该是一个立体图
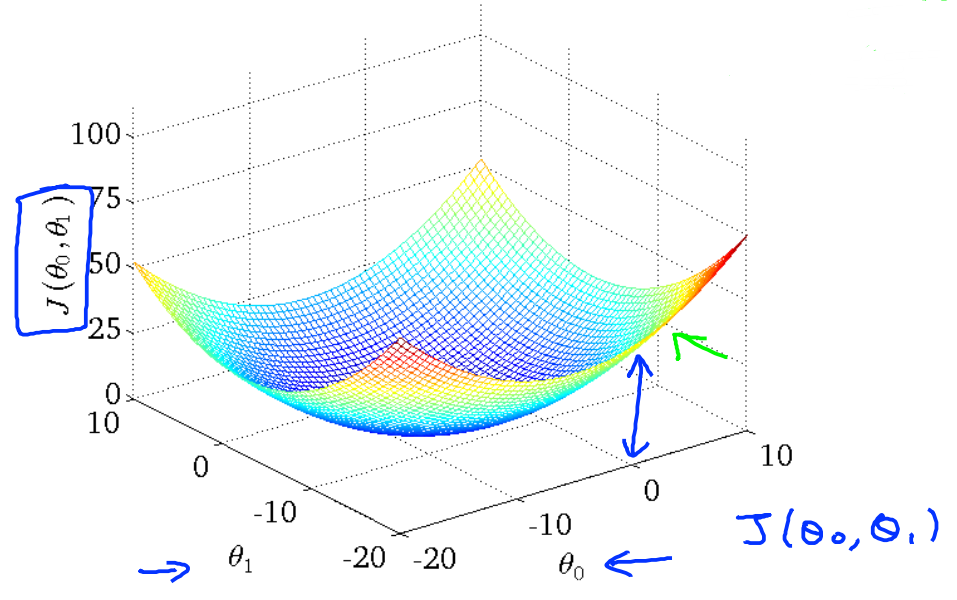
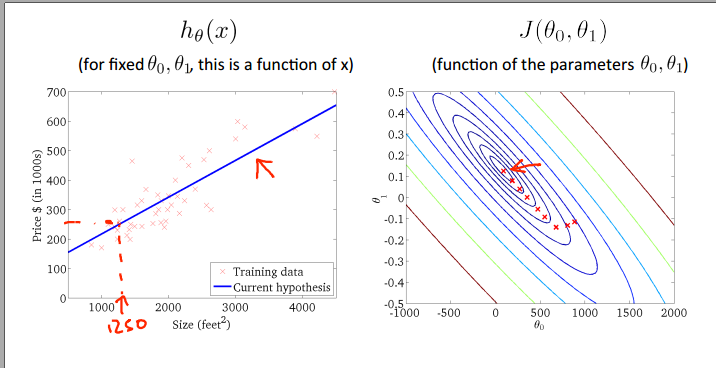
也可以用等高线图来表示
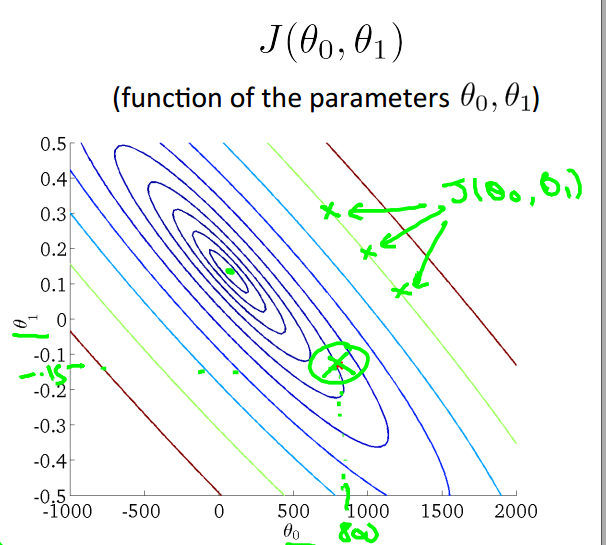
等高线图中椭圆边上的每一个点都代表相同值的\(J(θ_0, θ_1)\)
那么容易想到,最小值就是这些椭圆共同的中心点
取等高线图中不同的点,可以得到不同的预测函数图像
图1:

图2:
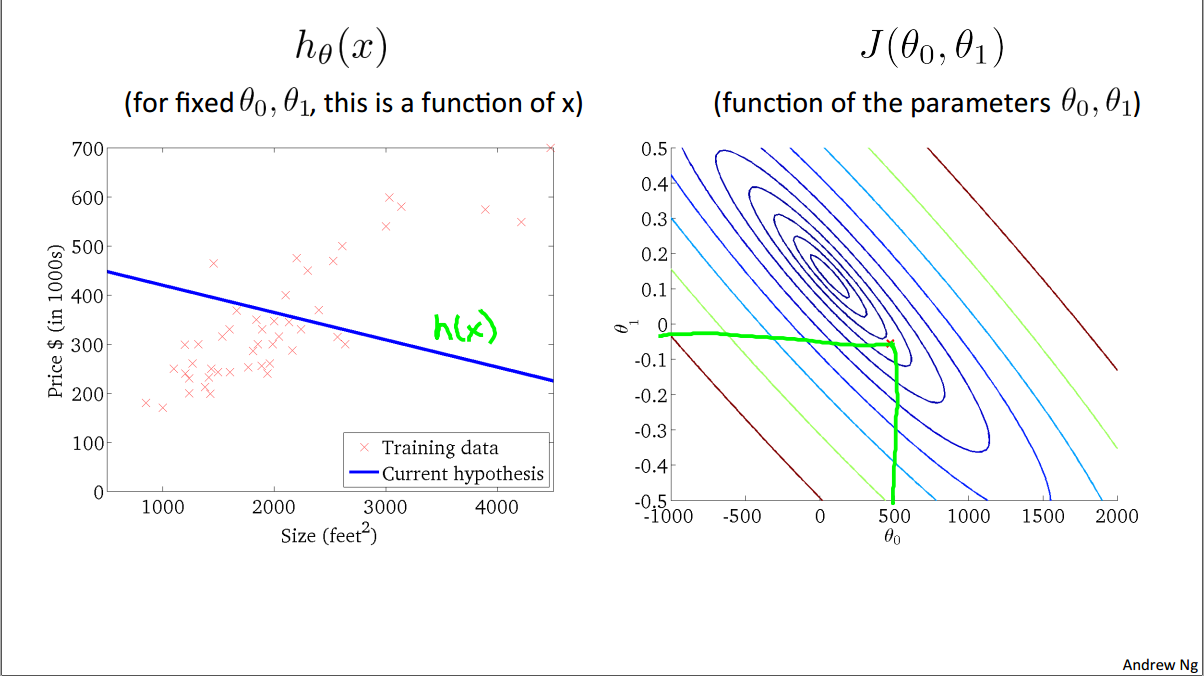
图3:

虽然预测函数图像可以看出。差值仍然不是最小,但已经尽可能接近最小值
梯度下降算法概览
梯度下降算法可以求出使得代价函数J值最小的$θ_j \((j=0,1,2,.....)
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
是一种很常用的算法,不仅被用在线性回归上,也广泛地应用于机器学习领域中的众多领域
首先,我们有一个代价函数J\)J(θ_0, θ_1)\(这个代价函数也许是线性回归模型中的代价函数,也许是其他模型的代价函数
我们要将之最小化,需要用到梯度下降算法
梯度下降算法甚至可以解决\)J(θ_0, θ_1,θ_2,......,θ_n)$这样的代价函数,因此梯度下降算法具有一般性
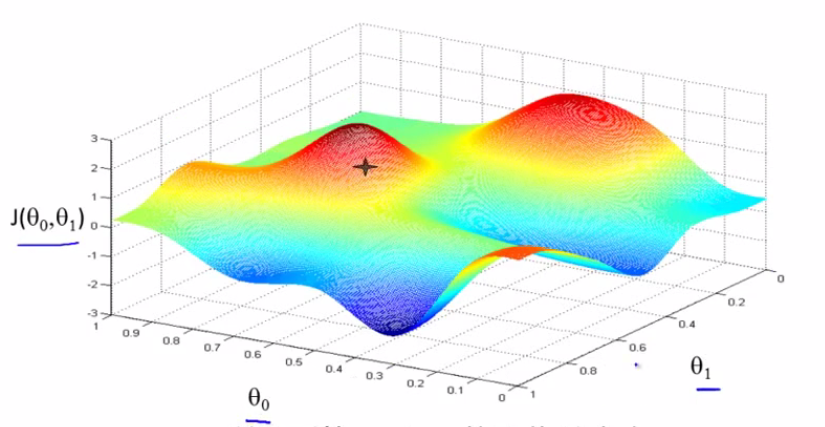
我们从图中红色处一点开始,想象自己在一座山上,想要尽快下山。
那么我们会选择下降得最快的路径
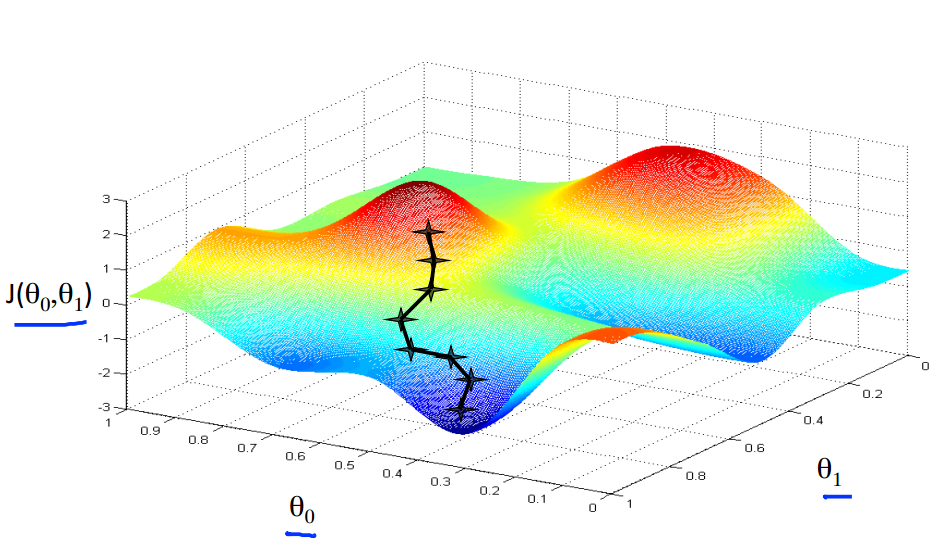
每一个点都是对于上一个点来说下降得最多的点。
这样最终会到达一个局部最小值(local minimum)
为什么是局部呢?
下面我们来选择另一个起始点
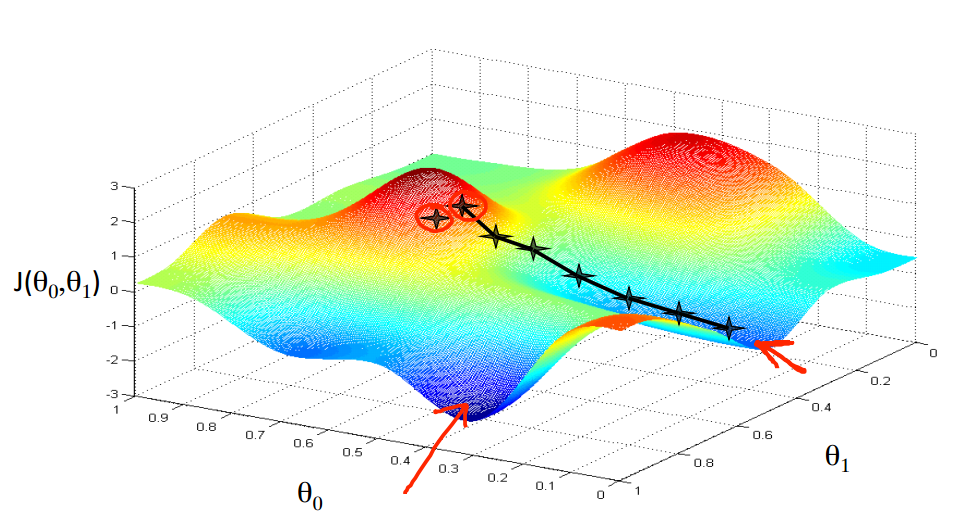
可以看出,我们最终到达了另一个完全不同的局部最小值(local minimum)
起始点位置的不同,最终会得到一个非常不同的局部最小值,这是梯度下降算法的特点
梯度下降算法的数学表达如下:
\(θ_j := θ_j - α\frac{
∂J(θ_0, θ_1)}{∂θ_j}\)
在此例中,j分别要取0和1
:=表示赋值。
α是学习速率,控制了梯度下降的速度。
显然在这个算法中,我们需要更新θ0和θ1的值,那么梯度下降算法的微妙之处在于,我们需要同时更新两个值,才能进行下一步梯度下降(下一次迭代)。
更新过程如下
\(temp0 := θ_0- α\frac{
∂J(θ_0, θ_1)}{∂θ_0}\)
\(temp1 := θ_1- α\frac{
∂J(θ_0, θ_1)}{∂θ_1}\)
$ θ_0 := temp0\(
\)θ_1 := temp1$
偏导数的意义
回到梯度下降算法的数学表达式上
\(θ_j := θ_j - α\frac{
∂J(θ_0, θ_1)}{∂θ_j}\)
几何意义上来说,函数中某点的倒数其实也就是那点切线的斜率,
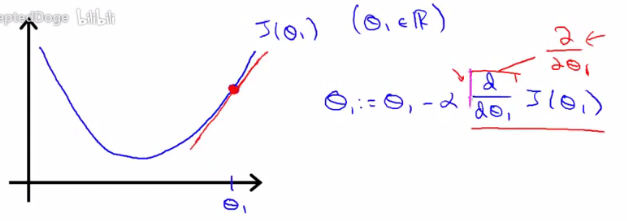
这个例子中是正斜率,也就是正导数,那么在梯度下降中,新θ值等于旧θ值减去α乘一个正数,θ向左移动

这个例子中是负斜率,也就是负导数,那么在梯度下降中,新θ值等于旧θ值减去α乘一个负数,θ向右移动
学习速率α
回到梯度下降算法的数学表达式上
\(θ_j := θ_j - α\frac{
∂J(θ_0, θ_1)}{∂θ_j}\)
因为α是偏导的系数,所以显然,α的大小会影响新θ值的大小,表现在图中应该是如此
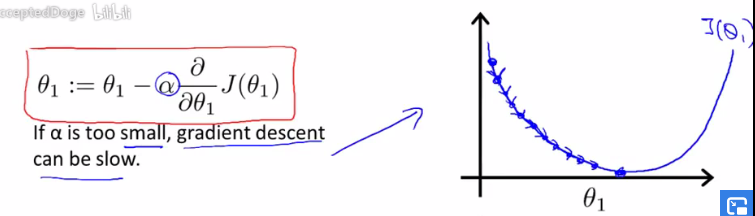
如果α特别小,那么每次更新都只会变化比较小的值
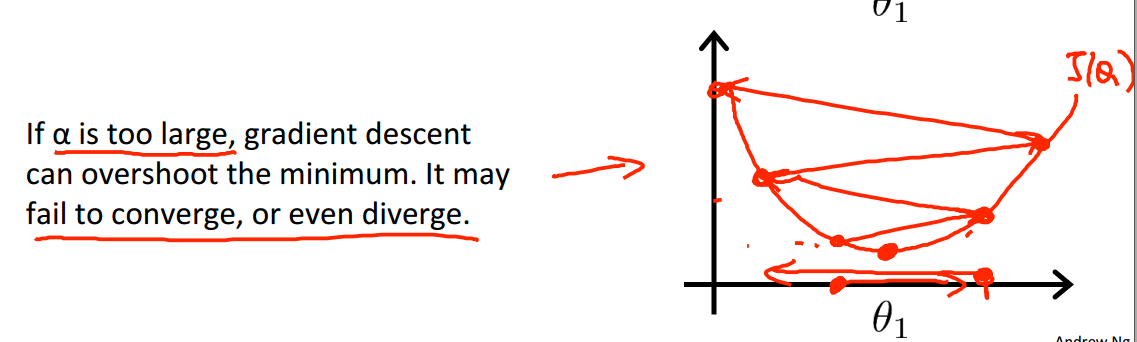
如果α特别大,那么每次更新都会变化比较大的值,那么就可能造成代价函数越来越大的坏结果
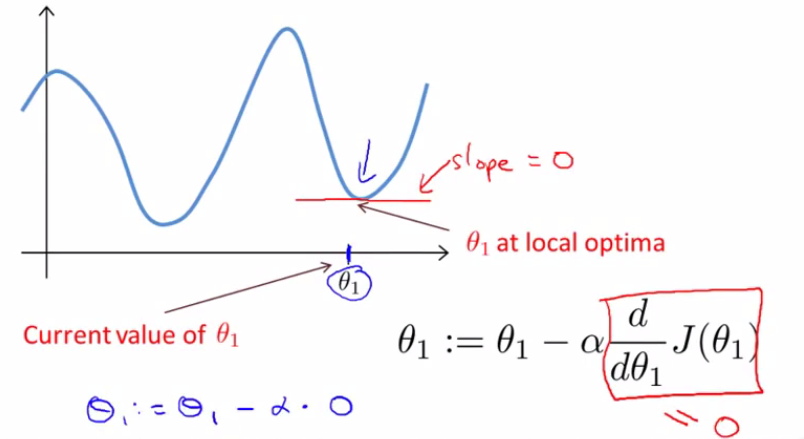
如果初始θ0, θ1位于局部最低点,那么梯度下降算法将不会更新θ的值
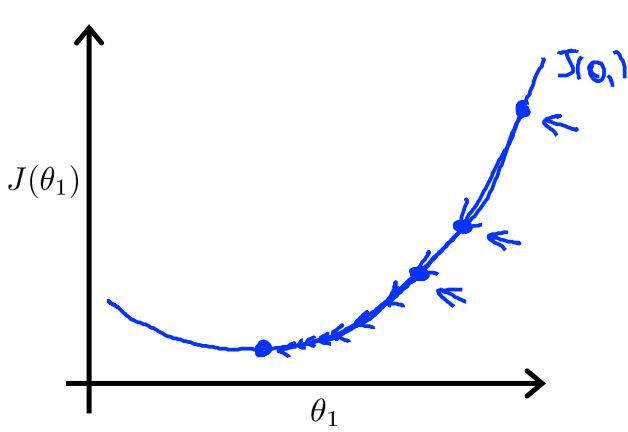
即使α固定且不过分大,梯度下降算法仍然可以收敛出局部最小值
因为如图所示,每次迭代,都会使当前点的导数值比上一点更小,所以最终仍然会得出局部最小值,随意没有必要每次都去更改α的值
在单元线性回归模型中的应用
其余前面都有,不再赘述
注意是对复合函数求偏导
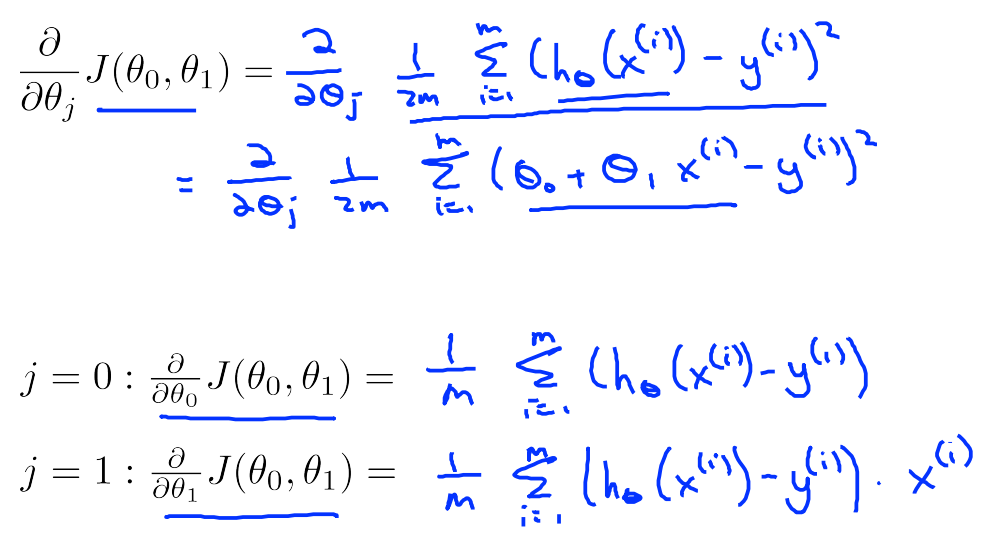
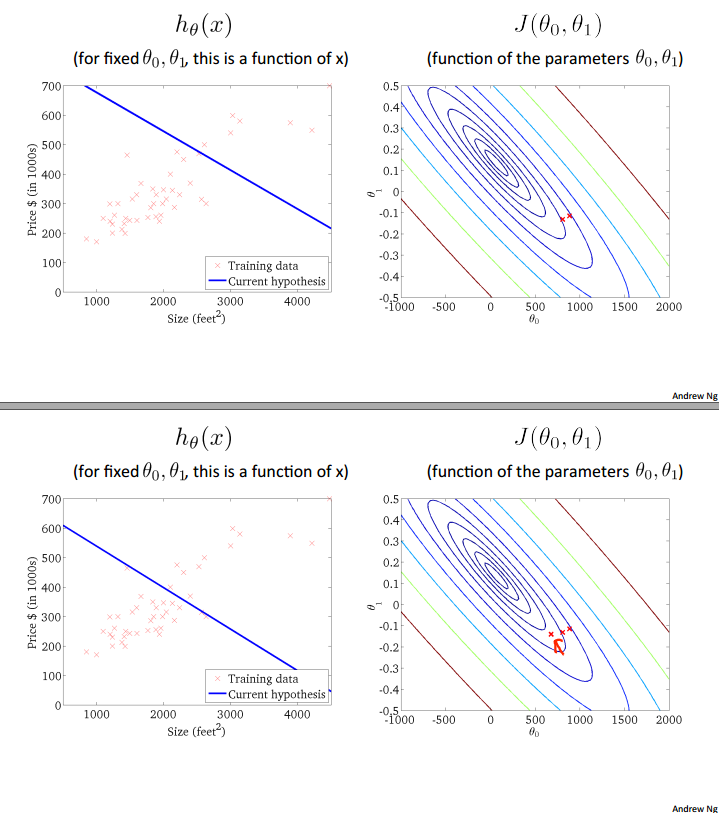
在等高线图中表示


 浙公网安备 33010602011771号
浙公网安备 33010602011771号