实验3 C语言函数应用编程
1. 实验任务1
task1.c
1 #include <stdio.h> 2 3 char score_to_grade(int score); // 函数声明 4 5 int main() { 6 int score; 7 char grade; 8 9 while (scanf_s("%d", &score) != EOF) { 10 grade = score_to_grade(score); // 函数调用 11 printf("分数: %d, 等级: %c\n\n", score, grade); 12 } 13 14 return 0; 15 } 16 17 // 函数定义 18 char score_to_grade(int score) { 19 char ans; 20 21 switch (score / 10) { 22 case 10: 23 case 9: ans = 'A'; break; 24 case 8: ans = 'B'; break; 25 case 7: ans = 'C'; break; 26 case 6: ans = 'D'; break; 27 default: ans = 'E'; 28 } 29 30 return ans; 31 }

问题1
函数功能: 将百分制分数转换为等级制成绩
-
90-100分:A
-
80-89分:B
-
70-79分:C
-
60-69分:D
-
60分以下:E
形参类型: int(整型)
返回值类型: char(字符型)
问题2
修改后的代码存在以下问题:
-
类型不匹配错误:
-
第3-6行中,
ans = "A"、ans = "B"等使用了双引号 -
"A"是字符串(字符数组),而ans是char类型变量 -
应该使用单引号:
'A'、'B'等
-
-
缺少break语句:
-
所有case分支都没有使用
break语句 -
会导致"穿透"现象,无论输入多少分,最终都会执行到default分支
-
结果总是返回'E'
-
-
格式问题:
-
第5行
case 7: ans = "C";case 6: ans = "D";写在同一行 -
虽然语法正确,但影响代码可读性
-
建议每个case单独一行
-
2. 实验任务2
task2.c
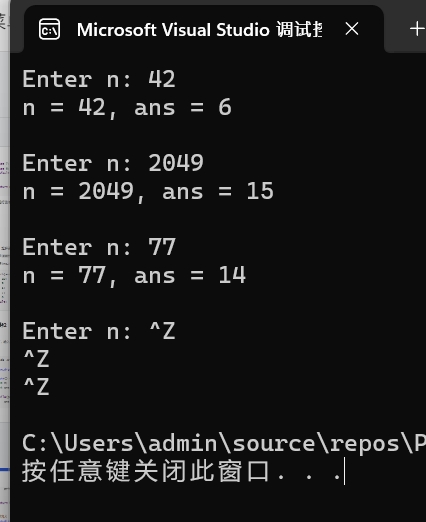
1 #include <stdio.h> 2 3 int sum_digits(int n); // 函数声明 4 5 int main() { 6 int n; 7 int ans; 8 9 while (printf("Enter n: "), scanf_s("%d", &n) != EOF) { 10 ans = sum_digits(n); // 函数调用 11 printf("n = %d, ans = %d\n\n", n, ans); 12 } 13 14 return 0; 15 } 16 17 // 函数定义 18 int sum_digits(int n) { 19 int ans = 0; 20 21 while (n != 0) { 22 ans += n % 10; 23 n /= 10; 24 } 25 26 return ans; 27 }
问题1
函数功能: 计算一个整数的各位数字之和
例如:
-
sum_digits(123)返回1+2+3 = 6 -
sum_digits(4567)返回4+5+6+7 = 22 -
sum_digits(9)返回9
问题2
能实现同样的输出。
两种实现方式的算法思维区别:
原实现(迭代/循环):
-
使用
while循环 -
算法步骤:
-
用
n % 10获取个位数并累加 -
用
n /= 10去掉已处理的个位数 -
重复直到
n == 0
-
-
思维特点:自底向上,逐步处理每一位数字
新实现(递归):
-
使用函数自我调用
-
算法逻辑:
-
基准情况:如果
n < 10(只有一位数),直接返回n -
递归情况:返回
sum_digits(n/10) + n%10-
sum_digits(n/10):计算去掉个位数后的数字和 -
n%10:当前个位数
-
-
-
思维特点:自顶向下,将问题分解为更小的同类问题
3. 实验任务3
task3.c
1 #include <stdio.h> 2 3 int power(int x, int n); // 函数声明 4 5 int main() { 6 int x, n; 7 int ans; 8 9 while (printf("Enter x and n: "), scanf_s("%d%d", &x, &n) != EOF) { 10 ans = power(x, n); // 函数调用 11 printf("n = %d, ans = %d\n\n", n, ans); 12 } 13 14 return 0; 15 } 16 17 // 函数定义 18 int power(int x, int n) { 19 int t; 20 21 if (n == 0) 22 return 1; 23 else if (n % 2) 24 return x * power(x, n - 1); 25 else { 26 t = power(x, n / 2); 27 return t * t; 28 } 29 }

问题1
函数功能: 计算整数x的n次幂(即 xⁿ)
例如:
-
power(2, 3)返回8(2³ = 8) -
power(5, 2)返回25(5² = 25) -
power(3, 0)返回1(任何数的0次方等于1)
问题2
是递归函数。
递归模式:
该函数使用了分治策略的递归模式,根据指数n的奇偶性采用不同的递归路径:
-
基准情况:
n == 0时,返回1 -
递归情况1(n为奇数):
n % 2为真时-
返回
x * power(x, n - 1)
-
-
递归情况2(n为偶数):
n % 2为假时-
计算
t = power(x, n / 2) -
返回
t * t
-
对应的数学公式模型:
power(x, n) =
⎧ 1, n = 0 (基准情况)
⎨ x × power(x, n-1), n为奇数 (递归情况1)
⎩ power(x, n/2)², n为偶数 (递归情况2)
4. 实验任务4
1 #include <stdio.h> 2 3 // 函数声明 4 int is_prime(int n); 5 6 int main() { 7 int count = 0; 8 9 printf("100以内的孪生素数:\n"); 10 11 // 从3开始检查,因为孪生素数从(3,5)开始 12 for (int n = 3; n <= 98; n++) { 13 if (is_prime(n) && is_prime(n + 2)) { 14 printf("%d %d\n", n, n + 2); 15 count++; 16 } 17 } 18 19 printf("\n100以内的孪生素数共有%d个。\n", count); 20 21 return 0; 22 } 23 24 // 函数定义:判断一个正整数n是否是素数 25 int is_prime(int n) { 26 // 小于2的数不是素数 27 if (n < 2) { 28 return 0; 29 } 30 31 // 2是素数 32 if (n == 2) { 33 return 1; 34 } 35 36 // 偶数(除了2)不是素数 37 if (n % 2 == 0) { 38 return 0; 39 } 40 41 // 检查奇数因子 42 for (int i = 3; i * i <= n; i += 2) { 43 if (n % i == 0) { 44 return 0; // 有因子,不是素数 45 } 46 } 47 48 return 1; // 是素数 49 }

5. 实验任务5
task5.c1
1 // 函数定义 - 迭代实现 2 #include <stdio.h> 3 int func(int n, int m); // 函数声明 4 5 int main() { 6 int n, m; 7 int ans; 8 9 while (scanf_s("%d%d", &n, &m) != EOF) { 10 ans = func(n, m); // 函数调用 11 printf("n = %d, m = %d, ans = %d\n\n", n, m, ans); 12 } 13 14 return 0; 15 } 16 17 // 函数定义 18 // 待补足。。。(分别用迭代和递归实现) 19 20 int func(int n, int m) { 21 // 特殊情况处理 22 if (m < 0 || m > n) return 0; 23 if (m == 0 || m == n) return 1; 24 25 // 使用组合数性质 C(n,m) = C(n,n-m) 减少计算量 26 if (m > n - m) m = n - m; 27 28 long long result = 1; 29 for (int i = 1; i <= m; i++) { 30 result = result * (n - i + 1) / i; 31 } 32 33 return (int)result; 34 }
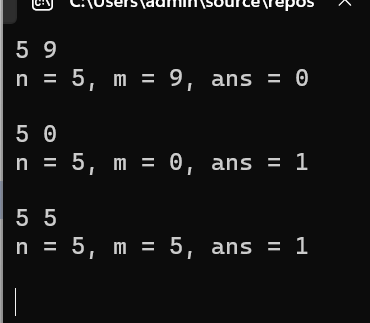
task5.c2
1 // 函数定义 - 迭代实现 2 #include <stdio.h> 3 int func(int n, int m); // 函数声明 4 5 int main() { 6 int n, m; 7 int ans; 8 9 while (scanf_s("%d%d", &n, &m) != EOF) { 10 ans = func(n, m); // 函数调用 11 printf("n = %d, m = %d, ans = %d\n\n", n, m, ans); 12 } 13 14 return 0; 15 } 16 17 // 函数定义 18 // 待补足。。。(分别用迭代和递归实现) 19 20 // 函数定义 - 递归实现 21 int func(int n, int m) { 22 // 边界条件 23 if (m < 0 || m > n) return 0; 24 if (m == 0 || m == n) return 1; 25 26 // 递归公式:C(n,m) = C(n-1,m-1) + C(n-1,m) 27 return func(n - 1, m - 1) + func(n - 1, m); 28 }

6. 实验任务6
task6.c
1 #include <stdio.h> 2 3 // 函数声明 4 int gcd(int a, int b, int c); 5 int gcd_two(int x, int y); 6 7 int main() { 8 int a, b, c; 9 int ans; 10 11 while (scanf_s("%d%d%d", &a, &b, &c) != EOF) { 12 ans = gcd(a, b, c); // 函数调用 13 printf("最大公约数: %d\n\n", ans); 14 } 15 16 return 0; 17 } 18 19 // 计算两个数的最大公约数(辅助函数) 20 int gcd_two(int x, int y) { 21 while (y != 0) { 22 int temp = y; 23 y = x % y; 24 x = temp; 25 } 26 return x; 27 } 28 29 // 计算三个数的最大公约数 30 int gcd(int a, int b, int c) { 31 // 先计算前两个数的gcd,再与第三个数计算gcd 32 return gcd_two(gcd_two(a, b), c); 33 }

7. 实验任务7
task7.c
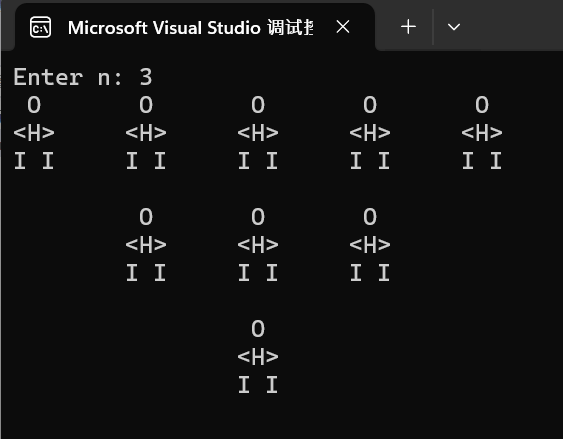
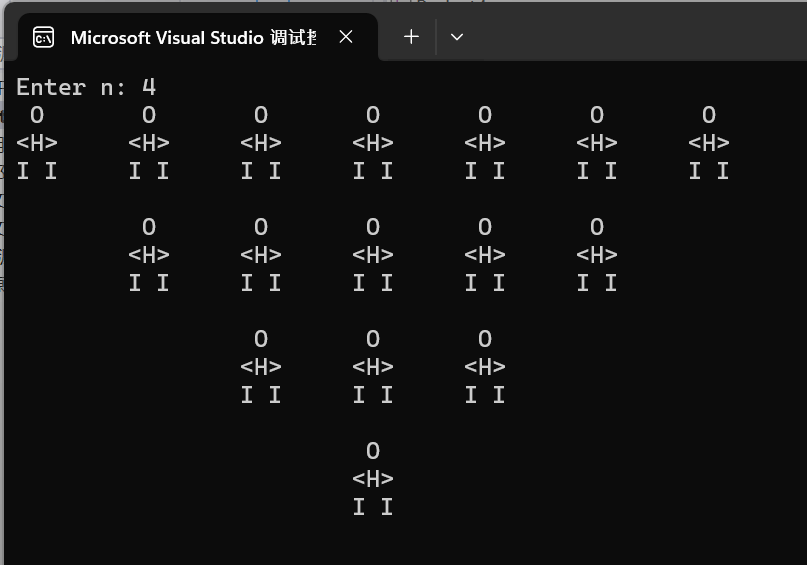
1 #include <stdio.h> 2 #include <stdlib.h> 3 void print_charman(int n); 4 int main() { 5 int n; 6 7 printf("Enter n: "); 8 scanf_s("%d", &n); 9 print_charman(n); 10 11 return 0; 12 } 13 14 void print_charman(int n) { 15 int i, j, k; 16 for (i = 0; i < n; i++) { 17 for (j = 0; j < i; j++) { 18 printf("\t"); 19 } 20 for (k = 1; k < 2 * (n - i); k++) { 21 printf(" O\t"); 22 } 23 printf("\n"); 24 for (j = 0; j < i; j++) { 25 printf("\t"); 26 } 27 for (k = 1; k < 2 * (n - i); k++) { 28 printf("<H>\t"); 29 } 30 printf("\n"); 31 for (j = 0; j < i; j++) { 32 printf("\t"); 33 } 34 for (k = 1; k < 2 * (n - i); k++) { 35 printf("I I\t"); 36 } 37 printf("\n\n"); 38 } 39 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号