实验三 函数的应用编程

1. 实验任务1

//运行下列程序，观察程序功能，体会用函数模块组织代码的好处
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <windows.h>
#define N 80
void print_text(int line, int col, char text[]); // 函数声明
void print_spaces(int n); // 函数声明
void print_blank_lines(int n); // 函数声明
int main() {
    int line, col, i;
    char text[N] = "hi, November~";
    srand(time(0)); // 以当前系统时间作为随机种子
    for (i = 1; i <= 10; ++i) {
        line = rand() % 25;  //产生0-24之间的随机整数，即小黑屏有25行
        col = rand() % 80;   //产生0-79之间的随机整数，即小黑屏有80列
        print_text(line, col, text);
        Sleep(1000); // 暂停1000ms
    }
    return 0;
}
// 打印n个空格
void print_spaces(int n) {
    int i;
    for (i = 1; i <= n; ++i)
        printf(" ");
}
// 打印n行空白行
void print_blank_lines(int n) 
{
    int i;
    for (i = 1; i <= n; ++i)
        printf("\n");
}
// 在第line行第col列打印一段文本
void print_text(int line, int col, char text[]) {
    print_blank_lines(line - 1); // 打印(line-1)行空行
    print_spaces(col - 1); // 打印(col-1)列空格
    printf("%s", text); // 在第line行、col列输出text中字符串
}
//程序功能在屏幕上做出跑动的字符小人的动画效果

运行效果截图

程序实现的功能：程序功能在屏幕上做出跑动的字符小人的动画效果

说明：对程序的理解已在程序代码中相关位置处以注释的形式给出

2. 实验任务2

（1）task2_1

//运行以下程序，理解局部静态变量在函数fac()中所起到的作用
// 利用局部static变量的特性，计算阶乘
#include <stdio.h>
long long fac(int n); // 函数声明
int main() {
    int i, n;
    printf("Enter n: ");
    scanf_s("%d", &n);
    for (i = 1; i <= n; ++i)
        printf("%d! = %lld\n", i, fac(i));
    return 0;
}
// 函数定义
long long fac(int n) 
{
    static long long p = 1;//定义局部静态变量p，每次重新进入函数，p都将保持上一次调用的值,不会重新被初始化为1,方便在主函数中通过循环实现阶乘的计算
    printf("p=%lld\n", p);
    p = p * n;
    return p;
}

运行效果截图

（2）task2_2

//思考如下程序的运行结果，并运行程序验证你的结果；
// 下述程序的运行结果为：
// 练习：局部static变量特性8,17
#include <stdio.h>
int func(int, int); // 函数声明
int main() {
    int k = 4, m = 1, p1, p2;
    p1 = func(k, m); // 函数调用，第一次调用，m=8
    p2 = func(k, m); // 函数调用，第二次调用，由于函数func()中存在静态局部变量，所以在第二次调用此函数时，该函数内部的静态局部变量将保持第一次被调用时的值而不会被重新初始化，所以此时m=17
    printf("%d, %d\n", p1, p2);
    return 0;
}
// 函数定义
int func(int a, int b) 
{
    static int m = 0, i = 2;//定义了两个静态局部变量m,i,并分别为其赋初值0，2；
    i += m + 1;
    m = i + a + b;
    return m;
}

运行效果截图

文字总结局部static变量的特性：局部静态变量的初始化是在程序的编译期间进行的，其在内存中位于静态存储区域，在程序运行期间其不会像局部变量一样在函数调用时才为其分配存储空间，而函数调用结束后其所占的内存立即被释放，所以局部静态变量会保持上一次函数调用时的值，而不是每一次调用函数都重新为其初始化。

说明:对程序的理解以及如何思考程序的运行结果已在代码中一注释的形式给出

3. 实验任务3

//设计一个递归函数模块用于计算指定数学表达式的值，补足递归函数定义部分，不能使用pow函数;
#include <stdio.h>
long long func(int n); // 函数声明
int main() {
    int n;
    long long f;
    while (scanf_s("%d", &n) != EOF) 
    {
        f = func(n); // 函数调用
        printf("n = %d, f = %lld\n", n, f);
    }
    return 0;
}
// 函数定义
// 待补足。。。

long long func(int n)  //根据递归表达式f(n)=f(n-1) + pow(2,n-1)编写递归函数
{
    int i,item=1;
    for (i = 1; i < n; i++)
        item = item * 2;      //计算每次递归中的pow(2,n-1)

    if (n == 0)
        return 0;
    else
        return func(n - 1) + item; //递归
}
//我允许一切发生

运行效果截图

说明：算法的设计思路已经在代码中以注释的形式给出

4. 实验任务4

//编写递归函数计算组合数，补全函数定义部分
#include <stdio.h>
int func(int n, int m);
int main() {
    int n, m;
    while (scanf_s("%d%d", &n, &m) != EOF)
        printf("n = %d, m = %d, ans = %d\n", n, m, func(n, m));
    return 0;
}
// 函数定义
// 待补足。。。
int func(int n, int m)
{
    //该功能是计算从n个不同元素中取出m个元素的组合数
    if (n == m) { return 1; }
    else if (n < m) { return 0; }        //列出此递归函数的所有出口
    else if (m == 0) { return 1; }
    else
        return func(n - 1, m) + func(n - 1, m - 1);

}

运行结果截图

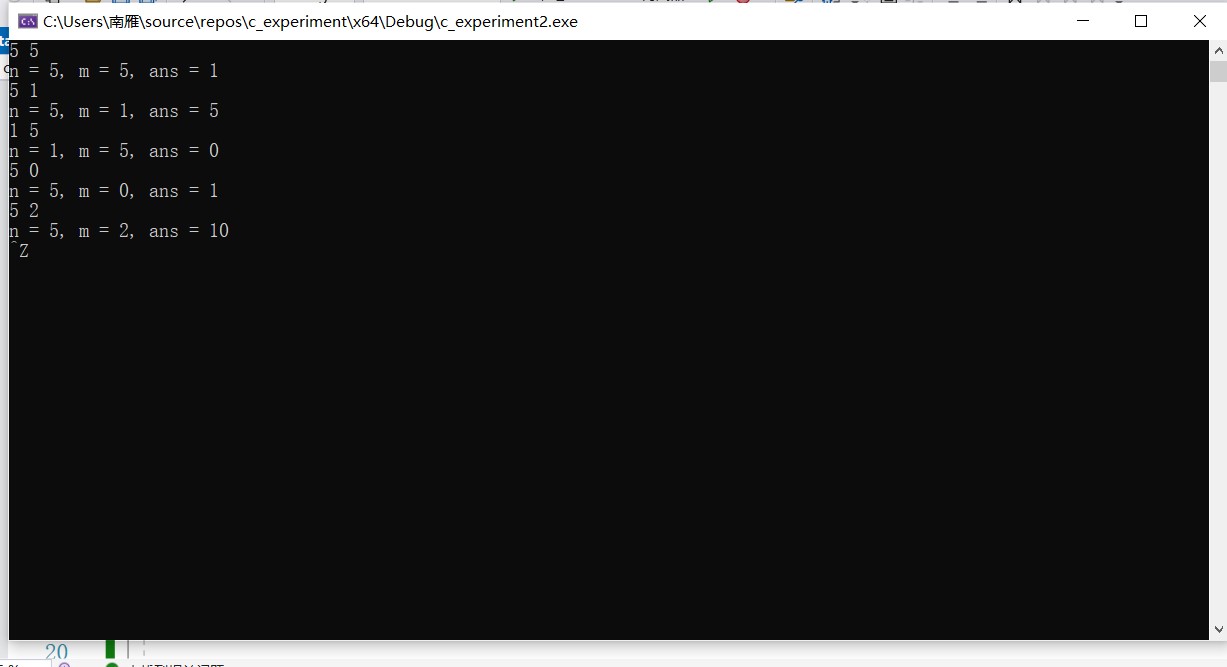
5. 实验任务5

//假如计算机没有乘法运算，编写递归函数mul实现计算两个整数m*n,补全代码定义部分
#include <stdio.h>
int mul(int n, int m);
int main() {
    int n, m;
    while (scanf_s("%d%d", &n, &m) != EOF)
        printf("%d * %d = %d\n", n, m, mul(n, m));
    return 0;
}
// 函数定义
//待补全。。。
int mul(int n, int m)     //根据递归表达式f(n,m)=f(n-1,m)+m或f(n,m)=f(n,m-1)+n编写递归函数；注意利用乘法交换律优化算法
{
    if (m >= n) 
    {
        if (n == 0)
            return 0;
        else
            return mul(n - 1,m) + m;

    }
    else
    {
        if (m == 0)
            return 0;
        else
            return mul(n, m - 1) + n;

    }
}

运行效果截图

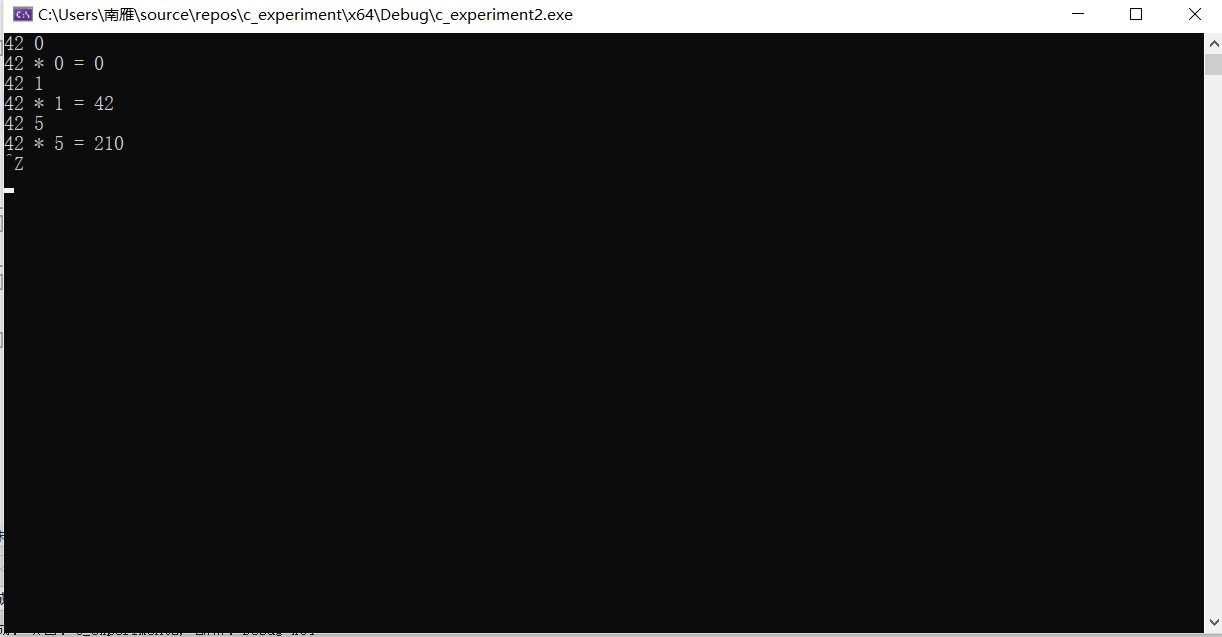
6. 实验任务6

//对教材「例4.9 Hanoi塔问题」稍做改写，使其满足以下要求：
//支持多组输入：输入不同的n值，打印输出不同的移动盘子方案
//对于每个n，除了打印盘子移动方案之外，还要打印输出移动盘子的总次数
//写体会
#include<stdio.h>
void moveplate(unsigned int n,char from,char to);
void hanoi(unsigned int n, char from, char temp, char to);
int count = 0;
int main()
{
    unsigned int n;
    printf("请输入你需要进行移动的盘子数：\n");
    while (scanf_s("%d", &n) != EOF)
    {
        printf("请输入你需要进行移动的盘子数：\n");
        hanoi(n, 'A', 'B', 'C');
        printf("移动盘子的总次数为：%d\n", count);
    }
    
    return 0;

}
void moveplate(unsigned int n, char from, char to) 
{
    printf("%u:%c-->%c\n", n, from, to);
    count++;
}
void hanoi(unsigned int n, char from, char temp, char to)
{
    if (n == 1)
        moveplate(n, from, to);
    else
    {
        hanoi(n - 1, from, to, temp);
        moveplate(n, from, to);
        hanoi(n - 1, temp, from, to);
    }
}

运行效果截图

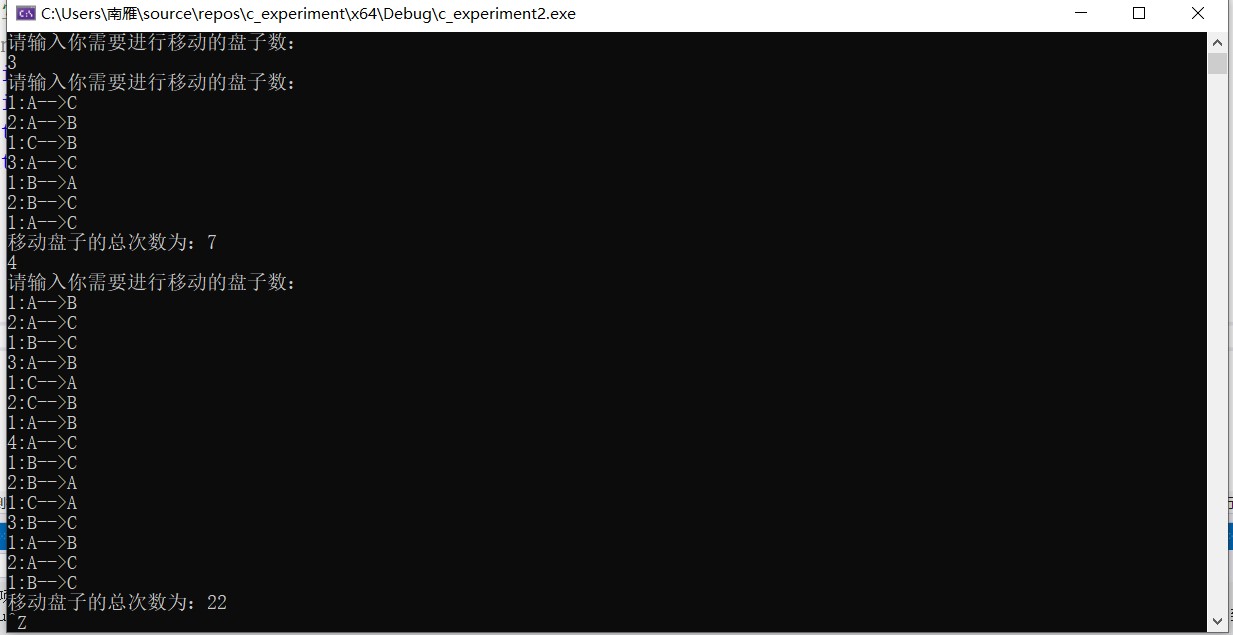
小总结：帮助我进一步加深对递归的思想的理解的就是此程序的Hanoi问题，也让我跳出我的思维定势，让我意识到学会把问题简化比死磕逻辑更重要，递归就是一步一步把复杂的问题化简的过程，直至该复杂问题已经不能再简化一眼就可以看出答案为止，所以设计一个递归函数我认为最关键的两步，第一推出递归表达式，这一步是设计递归函数的核心，而是找准“最简”及递归函数的出口。

7. 实验任务7

//编写程序task7.c，验证哥德巴赫猜想：任一充分大的偶数，可以用两个素数之和表示。具体要求如下：
//要求编写函数is_prime()用于判断一个整数n是否是素数。如果是，返回1；否则，返回0。
//在main()函数中调用函数is_prime()编写主体代码逻辑，用20以内的数验证哥德巴赫猜想。
//打印出20以内的数用两个素数之和表示的表达式。
#include<stdio.h>
int is_prime(int n);
int main()
{
    int i, j;
    for (i = 1; i <= 20; i++)
    {
        if (i % 2 == 0)
        {
            for (j = 1; j <= i; j++)//把所有相加都为偶数i的两个数遍历一遍输出满足条件的值；
            {
                if (is_prime(j) && is_prime(i - j) && (j<=(i-j)))        //i=j + (i-j),判断i,i-j是否均为素数；
                    printf("%d=%d+%d\n", i, j, i - j);
            }
        }
    }
    return 0;

}
int is_prime(int n)
{
    int i;
    if (n <= 1)
        return 0;
    for (i = 2; i < n; i++)
        if (n % i == 0)
            return 0;
    return 1;
}

运行效果截图

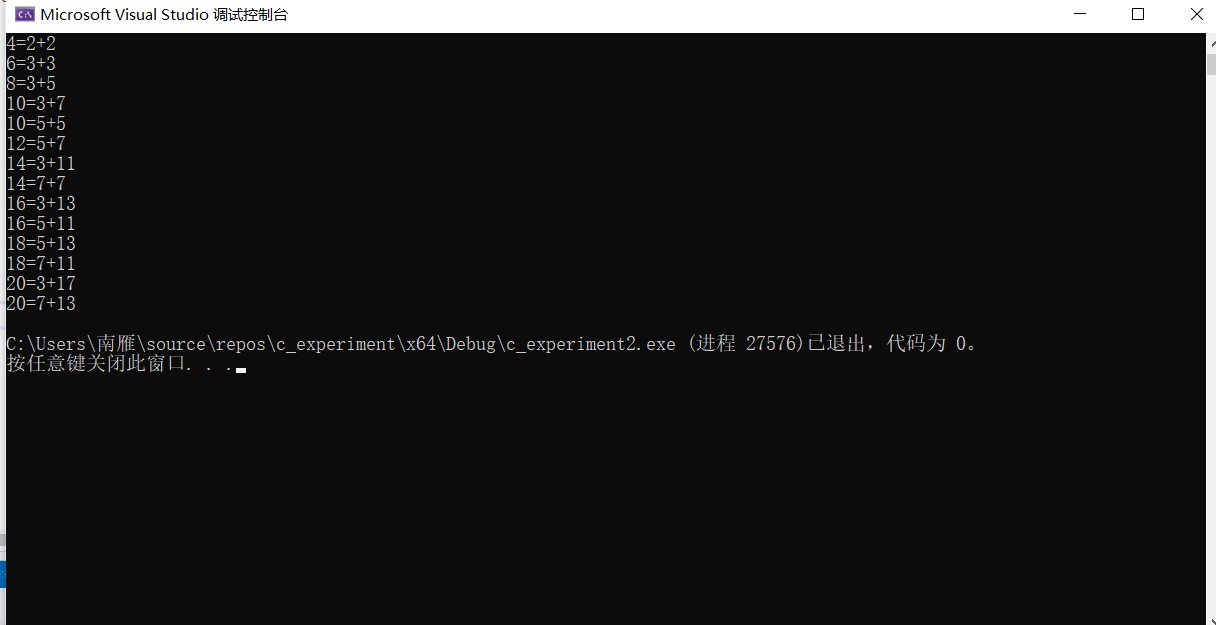
说明：算法的设计思路已在程序中以代码的形式给出

8. 实验任务8

//写反思*********
//编写函数func，实现将一个长整型数s的每一数位上的奇数依次取出来，构成一个新的数，高位仍在高位，低位仍在低位，返回这个新数。
//例如，s = 20211124时，调用函数fun后，返回111。
//在主函数中，通过多组输入方式，多次调用fun()，实现对多组数据的测试
#include <stdio.h>
#include<math.h>   
long fun(long s); // 函数声明
int main() {
    long s, t;
    printf("Enter a number: ");
    while (scanf_s("%ld", &s) != EOF) 
    {
        t = fun(s); // 函数调用
        printf("new number is: %ld\n\n", t);
        printf("Enter a number: ");
    }
    return 0;
}
// 函数定义
// 待补足。。。
long fun(long s)
{
    long a,count=0,b=0;
    
    do
    {
        a = s % 10;
        if (a % 2 != 0)
        {
            b = b + a*pow(10,count);
            count++;
        }
        s = s / 10;
    } while (s != 0);
    return b;
}

运行效果截图

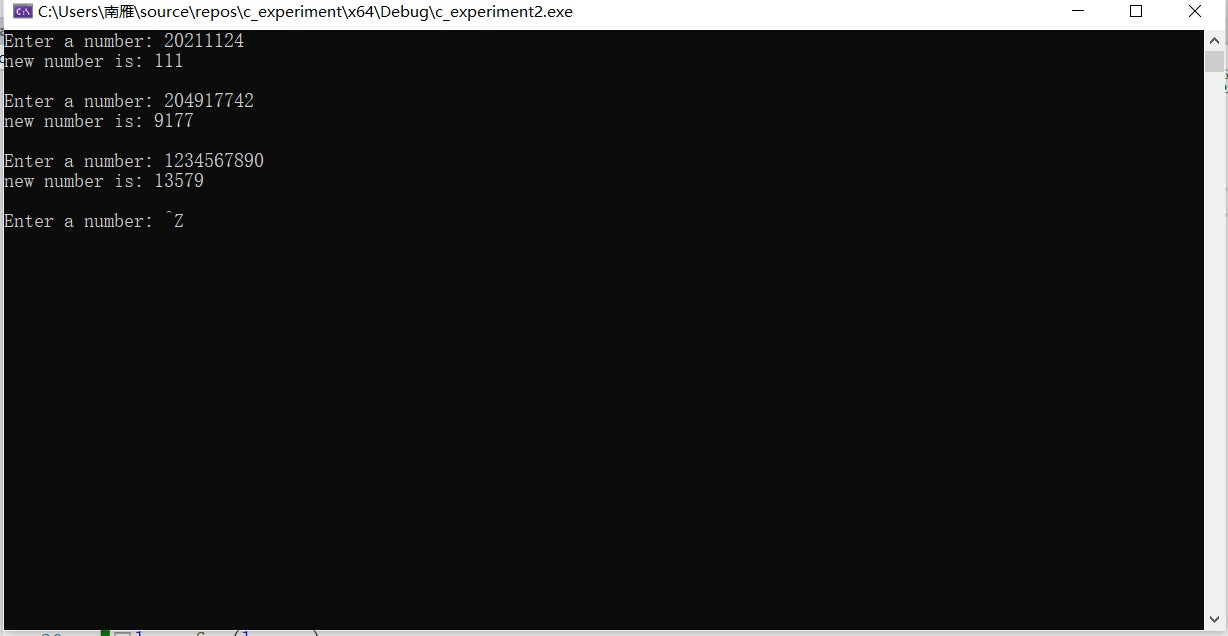
小反思：这题用到了库函数pow()但是却没有将相应的头文件包含进去，导致刚开始程序运行一直出错，但是检查算法逻辑一直都检查不出错误，所以注意细节