最大密度子图

模型描述

一张无向图\(G = (V, E)\)，没有点权也没有边权。

选取一个子图，使得\(\frac{|E'|}{|V'|}\)最大。

注意：这里的子图指的是，选取一些点，与之相关的边不一定全选。但是如果选取了某条边，那么其两个顶点必选。

但是因为全选与这些点相关的边，肯定是最优的，于是下文就默认是全选的。

解决方法

利用01分数规划的方法，原问题可以转化为最大化\(|E'| - \lambda |V'|\)，即最小化\(\lambda |V'| - |E'|\)

对于这个式子的化简，需要应用到一个技巧，就是把每条边拆成两份，两个端点分别占有一份。

\[\begin{aligned} \lambda |V'| - |E'| &= \sum_{v \in V'} g - (\frac{\sum_{v \in V'} deg(v)}{2} - \frac{c[V', \bar{V'}]}{2}) \\ &= \frac{1}{2}(\sum_{v \in V'}(2g - deg(v)) + c[V', \bar{V'}]) \end{aligned} \]

这里\(\bar{V'}\)是\(V'\)的补图，\(deg(v)\)是点\(v\)的度数。

下面就可以建图了，原图的每一条边对应成流网络中一条容量是\(1\)的边。每个点向虚拟汇点\(t\)连容量是\(2g - deg(v) + U\)的边，这里的\(U\)是一个自己设置的常数，目的是使得容量恒大于\(0\)。

设置一个虚拟源点\(s\)，向每个点连容量是\(U\)的边。如图所示：

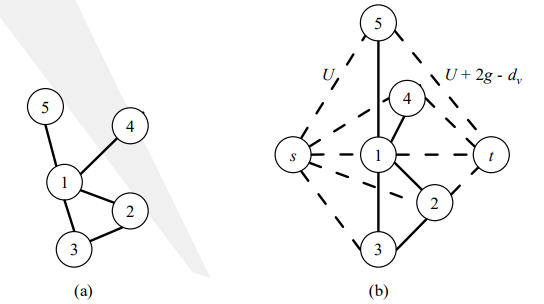
下面证明结果的最优性：

令\(V' = S - {s}, \bar{V'} = V - V'\)

\[\begin{aligned} c[S, T] &= \sum_{u \in \bar{V'}} U + \sum_{u \in V'}(2g - deg(u) + U) + \sum_{u \in V'}\sum_{v \in \bar{V'}}c_{u,v} \\ &= \sum_{u \in \bar{V'}} U + \sum_{u \in V'}(2g - deg(u) + U + \sum_{v \in \bar{V'}}c_{u,v}) \\ &= (\sum_{u \in \bar{V'}} U + \sum_{u \in V'} U) + 2g\sum_{u \in V'} - \sum_{u \in V'}\sum_{v \in V'}c_{u,v} \\ &= nU + 2g|V'| - 2|E'| \end{aligned} \]

因此，\(|E'| - \lambda |V'| = \frac{nU - c[s, t]}{2}\)

模型拓展

若有边权

目标式子改为\(\frac{\sum_{e \in E'} w_e}{|V'|}\)。

只需要重新定义一下\(deg(v)\)即可，定义\(deg(v)\)为以\(v\)为顶点的边的边权和。

若有点权

目标式子改为\(\frac{\sum_{e \in E'} w_e + \sum_{v \in V'} p_v}{|V'|}\)

重新推导目标式子为：\(\frac{1}{2}(\sum_{v \in V'}(2g - deg(v) - 2p_v) + c[V', \bar{V'}])\)

\(v\)到\(t\)的边权改为\(2g - deg(v) - 2p_v + U\)。其他不变。