给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。
示例 1:
输入: "babad" 输出: "bab" 注意: "aba"也是一个有效答案。
示例 2:
输入: "cbbd" 输出: "bb"
自己的思路:求一个字符串的最长回文子串,我们可以将以每个字符为首的子串都遍历一遍,判断是否为回文,如果是回文,再判断最大长度的回文子串。算法简单,但是算法复杂度太高,O(n^3)
string longestPalindrome(string s) { if(s.empty()) return ""; if(s.size()==1) return s; int start=0,maxlength=1;//记录最大回文子串的起始位置以及长度 for(int i=0;i<s.size();i++) for(int j=i+1;j<s.size();j++)//从当前位置的下一个开始算 { int temp1,temp2; for(temp1=i,temp2=j;temp1<temp2;temp1++,temp2--) { if(s[temp1]!=s[temp2]) break; } if(temp1>=temp2 && j-i+1>maxlength)//这里要注意条件为temp1>=temp2,因为如果是偶数个字符,相邻的两个经上一步会出现大于的情况 { maxlength = j-i+1; start=i; } } return s.substr(start,maxlength);//利用string中的substr函数来返回相应的子串,第一个参数是起始位置,第二个参数是字符个数 }
很明显上述的算法复杂度太高,应该有更加快捷的做法来处理。下面介绍两种方法
(1)DP
动态规划的方法,我会在下一篇单独来介绍,这里只说明此题的DP代码
对于字符串str,假设dp[i,j]=1表示str[i...j]是回文子串,那个必定存在dp[i+1,j-1]=1。这样最长回文子串就能分解成一系列子问题,可以利用动态规划求解了。首先构造状态转移方程
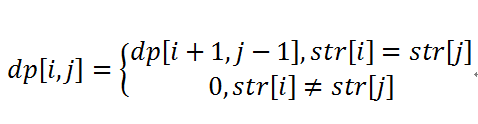
上面的状态转移方程表示,当str[i]=str[j]时,如果str[i+1...j-1]是回文串,则str[i...j]也是回文串;如果str[i+1...j-1]不是回文串,则str[i...j]不是回文串。
初始状态
- dp[i][i]=1
- dp[i][i+1]=1 if str[i]==str[i+1]
上式的意义是单个字符,两个相同字符都是回文串。
string longestPalindrome(string s) { if (s.empty()) return ""; int len = s.size(); if (len == 1)return s; int longest = 1; int start=0; vector<vector<int> > dp(len,vector<int>(len)); for (int i = 0; i < len; i++) { dp[i][i] = 1; if(i<len-1) { if (s[i] == s[i + 1]) { dp[i][i + 1] = 1; start=i; longest=2; } } } for (int l = 3; l <= len; l++)//子串长度 { for (int i = 0; i+l-1 < len; i++)//枚举子串的起始点 { int j=l+i-1;//终点 if (s[i] == s[j] && dp[i+1][j-1]==1) { dp[i][j] = 1; start=i; longest = l; } } } return s.substr(start,longest); }
这里我们需要用一个二维数组dp来作为备忘录,记录子问题的结果,以便重复的计算。这也是动态规划的精髓所在。不过这种做法的算法复杂度也是O(n^2)
(2)Manacher法
这是一个专门用作处理最长回文子串的方法,思想很巧妙,比较难以理解,这里直接借用了别人的讲解方法。其实主要思想是,把给定的字符串的每一个字母当做中心,向两边扩展,这样来找最长的子回文串,这个叫中心扩展法,但是这个方法还要考虑到处理abba这种偶数个字符的回文串。Manacher法将所有的字符串全部变成奇数个字符。
Manacher算法原理与实现
下面介绍Manacher算法的原理与步骤。
首先,Manacher算法提供了一种巧妙地办法,将长度为奇数的回文串和长度为偶数的回文串一起考虑,具体做法是,在原字符串的每个相邻两个字符中间插入一个分隔符,同时在首尾也要添加一个分隔符,分隔符的要求是不在原串中出现,一般情况下可以用#号。下面举一个例子:
(1)Len数组简介与性质
Manacher算法用一个辅助数组Len[i]表示以字符T[i]为中心的最长回文字串的最右字符到T[i]的长度,比如以T[i]为中心的最长回文字串是T[l,r],那么Len[i]=r-i+1。
对于上面的例子,可以得出Len[i]数组为:
Len数组有一个性质,那就是Len[i]-1就是该回文子串在原字符串S中的长度,至于证明,首先在转换得到的字符串T中,所有的回文字串的长度都为奇数,那么对于以T[i]为中心的最长回文字串,其长度就为2*Len[i]-1,经过观察可知,T中所有的回文子串,其中分隔符的数量一定比其他字符的数量多1,也就是有Len[i]个分隔符,剩下Len[i]-1个字符来自原字符串,所以该回文串在原字符串中的长度就为Len[i]-1。
有了这个性质,那么原问题就转化为求所有的Len[i]。下面介绍如何在线性时间复杂度内求出所有的Len。
(2)Len数组的计算
首先从左往右依次计算Len[i],当计算Len[i]时,Len[j](0<=j<i)已经计算完毕。设P为之前计算中最长回文子串的右端点的最大值,并且设取得这个最大值的位置为po,分两种情况:
第一种情况:i<=P
那么找到i相对于po的对称位置,设为j,那么如果Len[j]<P-i,如下图:
那么说明以j为中心的回文串一定在以po为中心的回文串的内部,且j和i关于位置po对称,由回文串的定义可知,一个回文串反过来还是一个回文串,所以以i为中心的回文串的长度至少和以j为中心的回文串一样,即Len[i]>=Len[j]。因为Len[j]<P-i,所以说i+Len[j]<P。由对称性可知Len[i]=Len[j]。
如果Len[j]>=P-i,由对称性,说明以i为中心的回文串可能会延伸到P之外,而大于P的部分我们还没有进行匹配,所以要从P+1位置开始一个一个进行匹配,直到发生失配,从而更新P和对应的po以及Len[i]。
第二种情况: i>P
如果i比P还要大,说明对于中点为i的回文串还一点都没有匹配,这个时候,就只能老老实实地一个一个匹配了,匹配完成后要更新P的位置和对应的po以及Len[i]。
2.时间复杂度分析
Manacher算法的时间复杂度分析和Z算法类似,因为算法只有遇到还没有匹配的位置时才进行匹配,已经匹配过的位置不再进行匹配,所以对于T字符串中的每一个位置,只进行一次匹配,所以Manacher算法的总体时间复杂度为O(n),其中n为T字符串的长度,由于T的长度事实上是S的两倍,所以时间复杂度依然是线性的。
下面是算法的实现,注意,为了避免更新P的时候导致越界,我们在字符串T的前增加一个特殊字符,比如说‘$’,所以算法中字符串是从1开始的。、
string longestPalindrome(string s) { string manaStr = "$#"; for (int i=0;i<s.size();i++) //首先构造出新的字符串
{ manaStr += s[i]; manaStr += '#'; } vector<int> rd(manaStr.size(), 0);//用一个辅助数组来记录最大的回文串长度,注意这里记录的是新串的长度,原串的长度要减去1 int pos = 0, mx = 0; int start = 0, maxLen = 0; for (int i = 1; i < manaStr.size(); i++) { rd[i] = i < mx ? min(rd[2 * pos - i], mx - i) : 1; while (i+rd[i]<manaStr.size() && i-rd[i]>0 && manaStr[i + rd[i]] == manaStr[i - rd[i]])//这里要注意数组越界的判断,源代码没有注意,release下没有报错 rd[i]++; if (i + rd[i] > mx) //如果新计算的最右侧端点大于mx,则更新pos和mx { pos = i; mx = i + rd[i]; } if (rd[i] - 1 > maxLen)
{ start = (i - rd[i]) / 2; maxLen = rd[i] - 1; } } return s.substr(start, maxLen); }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号