第六讲-参数方程与极坐标

---

这里介绍了参数方程的引入原因，并介绍了不同曲线的直角坐标方程和参数方程的转化，以及另一种极坐标方程表示方法。

即表示方法不唯一，也没有最好，适当选择。

并介绍了圆锥曲线（抛物线、圆、椭圆、双曲线）的积坐标定义并推导成直角坐标形式。

 

曲线的参数方程

 

1. 参数方程概念

 

• 一元函数  的图形通常为平面曲(显式表示法)

 

 

 

 

• 平面上满足方程 的集合通常表示一条平面曲线(隐式方程、直角坐标方程)

 

 

 

 

竖直判别法

 

一元函数这种显式表示的函数图形需要满足竖直判别法：函数的图形与任何一条平行于y轴的直线不能有一个以上的交点.

 

通过竖直判别法，显然圆、笛卡尔叶形线或大多数的曲线都不符合要求，那么在后面涉及到复杂曲线计算时如何表示这样的平面曲线呢？既然一个方程不能够表示这样的平面曲线，那能不能用多个方程来表示平面曲线呢？这样由多个方程表示平面曲线的方程就是曲线参数方程

 

 

 

 

2. 直角坐标方程化为参数方程

 

• 直接将横坐标或者纵坐标作为参数

 

 

 

 

 

• 令

   

   

  ，代入直角坐标方程解 x 为 t 的关系式得

 

 

 

 

 

 

• 利用三角恒等式

• 由几何意义或者问题的实际背景

 

 

 

 

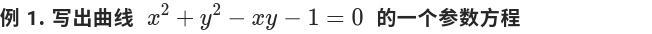
例 2. 求圆滚线的参数方程

 

• 关键点: 因为都是一个点跑过的路程
  

   

   

  

   

   

 

 

3. 常见的参数方程

 

 

 

 

 

 

 

例 3. 将曲线参数方程化为直角坐标方程

 

 

• 星形线性质: 星形线的切线介于坐标轴之间的线段是不变的. 这样的概念与圆滚线类似，与圆滚线在一条直线上运动不同，星形线则是通过一个小圆沿着更大的一个圆的内侧滚动滚动一周，此时圆上的一点同样也可以形成一条相应的曲线轨迹

 

---

 

极坐标与极坐标方程

 

1. 极坐标

 

• 直角坐标系与极坐标系的关系

 

 

 

 

 

 

 

 

 

 

 

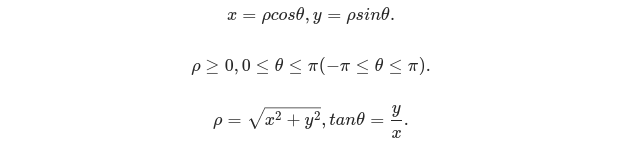
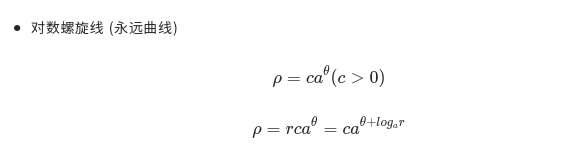
第二条方程是在第一条基础上乘以一个常数 r，通过变形，常系数变成了变量的指数。对原来的方程乘上一个常数，原来的方程所对应的曲线进行放大或者缩小，这样的变化过程通过方程的变形我们可以发现，原来角的起点变为了一个新的值，这意味着原来的方程所对应的曲线经过旋转后，可以让它和原来的曲线进行重合

 

 

 

 

性质: 将对数螺旋线做相似放大或缩小，均能与原曲线重合.

 

2. 曲线的极坐标表示

记住：p>0

 

 

 

---

 

圆锥曲线

 

圆锥曲线的几何定义

 

 

 

 

 

圆锥曲线的极坐标方程