动态规划优化初步（一） 四边形不等式

首先祝贺一下本猪的博客终于开通了啊～～溜过这扇门花了不少时间啊～

（对了，作为一个ACG爱好者，本猪会不停的捏他&吐槽，捏他会注明出处…比如上面那个就出自《きっと、澄みわたる朝色よりも、》，欢迎吐槽～～）

其实是受BobHan的推荐来这里的，他的博客在 这里 。去了请狂踩，不用客气。

（BobHan：就你想得出这种邀请方式！Pia飞很远……）

 

由于本猪只是一个弱弱，理解存在偏差之处，若有错误请指出，本猪期待您的斧正～

文章啥的版权没有，欢迎转载，如果可以最好能注明出处～

 

这篇文章主要会讲四边形不等式的理解，没有任何理论证明，代码等。已经理解的童鞋请不要浪费人参。

 

四边形不等式用于权值函数符合一定条件的区间型动态规划。

（众同学：一定条件是什么啊？？是神马啊？？你不说咱怎么知道啊？？偶：就是w[i,j] + w[i’，j’] <= w[i’,j] + w[i,j’]  (i<=i’<j<=j’) 啦。）

 

首先 按照本猪的理解 四边形不等式 其实是一个拓展的排序不等式。

(其实只是有点类似而已 证明方法神马的，完全都不一样……,被Pia飞)

真相是：四边形不等式其实就是一个证明单调性的过程 但是这样说不容易理解……

(众同学：你这样讲我们更不理解！！自己Pia飞！偶：～～！！)

 

tip1：排序不等式：若a1>a2>a3>……>an>0,b1>b2>b3>……>bn>0那么

a1*b1+a2*b2+……+an*bn>=a1*b2+a2*b3+……+an-1*bn+an*b1>=……>=a1*bn+a2*b1+a3*b2+……+an*bn-1

云云……就是这样，简单的说就是“顺序和大于乱序和”。

（众同学：这个数学课上讲过！！不用你丫的废话～～Pia飞……）

（弱弱的补一句：其实物理上热学的时候也讲过……众同学：不就是热二吗，你废话真多！！再次Pia飞……）

 

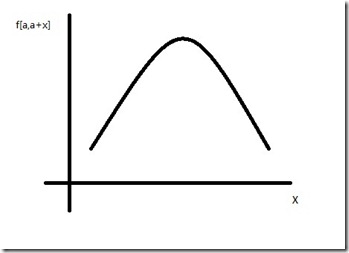
然后 抛开那些烦人的证明 我们来看 如果dp数组f[]符合四边形不等式 那么它其中f[x,a+x]的图像连起来应该像这样(为什么你就别管了，先看)：

图像像这样其实和权值函数有关系。具体的可以调试代码时慢慢体会，不过一般不明显=.=|||，原因在下面：

中间可能有若干起伏（并不是完全的先单调上升然后下降，但总体趋势是这样，为了示意就先表示成这样吧。众同学：严谨啊，严谨！！Pia飞……）

同理，它的相同长度的亲戚区间的图像也应该类似。（某童鞋：偶怎么想到团子大家族……）（《Clannad》，就是《家族》，著名催泪弹）

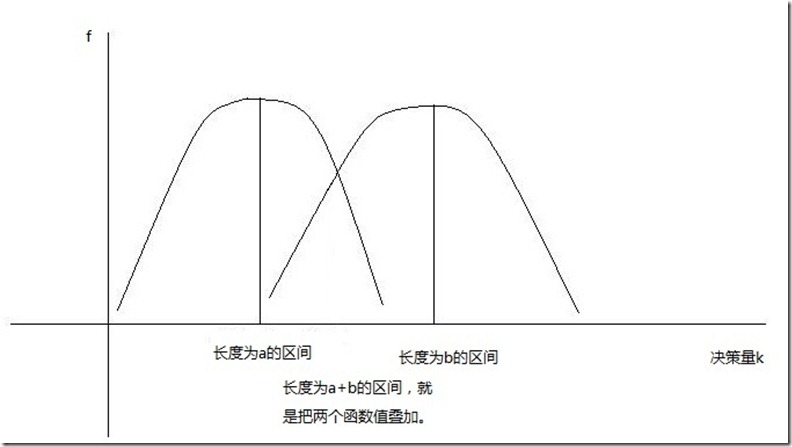
然后我们来看，如果区间长度变大，就要合并两个较小的区间

 

从单调性可以看出来，大区间的决策夹在两个小区间之间。在a的决策量之前，两个函数全都是单调上升，b的决策量之后，两个函数全都是单调下降。

这就是网上的某篇论文里说的：

四边形不等式其实就是一个证明单调性的过程

（众人：到底有多少实质啊！！Pia飞！！偶：这是因人而异的=.=|||）

在前面提那个排序不等式 实际上也是提到了一个单调性的问题。只不过两个上升的数列换成了两个先上升后下降的数列。

 

到这里大家应该都能“理解”了吧，嗯嗯，嘿嘿嘿（眼旁一道亮光闪过，又成功误导一位小盆友），你们去找一题做下，比如合并狮子、最优二叉搜索树，就会发现，f的情况其实很复杂，并不像上面所说那么简单。关于严谨的证明请看这里（赵爽同学的论文，115下载，理论永久，pdf）。把这个证明看懂了你四边形不等式就只差代码啦～

（众同学：合并狮子？偶：石子，不是Saber的宠物……=.=|||，然后死很远……）（《Fate/stay night》）

 

由于只是讲一下思想，就不贴代码了，网上可以找到很多。（弱弱的说一句：其实是因为代码太丑了……还是菜鸟风格，一点长进都没有……）

（众同学：吃了你哦！！）（《初音ミク Project DIVA 2nd》 歌曲《爱言叶》）

 

四边形不等式这种东西，就记住，满足“一定条件”的区间DP，大区间的决策在两小区间之间。一般这样就OK啦～当然拓展啥的不包括在内。

 

顺手送上网上找到的一点资料，不过方程好像有点崩坏……凑合着看看也不错～传送门（115下载，理论永久，doc）

 

四边形不等式是一个很神奇的东西～做做题就明白了（众同学：能做题还有啥不明白啊！你个白痴！某游戏帝：手柄斩！！）（《旋风管家》）

 

（灰溜溜的掩面逃走……Byene~~）