2A-1.霍夫变换
霍夫变换
参数化模型
霍夫变换是一种参数化模型的方法,所谓参数化模型,即带参数的模型,它能表示一类模型,其中每个模型由不同的参数值定义。比如直线、圆、甚至参数化模板。
举例说明,比如同一条直线上的点对应相同的模型,而不同直线的斜率和距离某个点的距离不同,那么在这里,斜率和距离为参数,他们对应不同的模型。
参数化模型的选择:
- 选择的模型能表达一组特征而不是单独一个特征
- 不能只根据一个点就能决定它属于哪个模型
- 验证一个参数化模型是不可行的(即使无限算力的电脑也不能验证所有符合这个模型的数据)
投票机制
投票机制是一种让特征自己选择与所有与之匹配的模型并进行投票的常用技术。步骤如下:
- 遍历特征,将特征转化为对模型参数值的投票
- 找到得到票数最多的几个模型
投票机制的可行性:
- 能够解决噪音问题:噪音也参与投票,但是他们会淹没在海量的真正的模型的投票中
- 即使有些特征没有被发现,模型也能将这些分散的片段连接起来
投票机制需要解决的问题:
- 给出一个点,能够判定它属于哪个直线
- 图像中有几条直线
- 哪些点属于哪些直线
霍夫变换的投票机制
- 每个边缘点投票给与之相关的点(投票给所有经过它的直线)
- 找到得到票数最多的几个模型
霍夫空间 - 检测直线
模型参数形成的空间
以直线为例,霍夫空间中的每个点对应一条直线,他们是对偶的
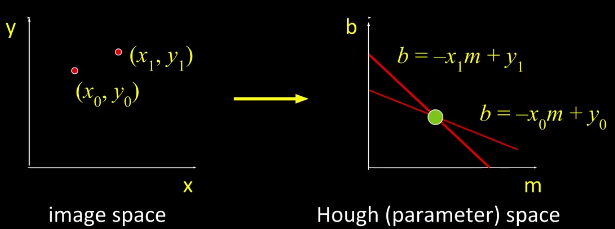
将每个点按照如上方法变换到霍夫空间,然后将霍夫空间划分为一些区间块,分别统计它们各自的投票数:
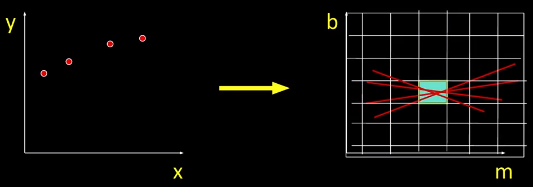
这种方法存在一个问题,就是当霍夫空间中的直线斜率无穷大时,直线将无法在霍夫空间中表示,其中一种解决方法是选择另外一种霍夫空间:\((\theta, d)\),\(\theta\) 是原点到直线垂线与x轴的夹角,d 是垂线距离
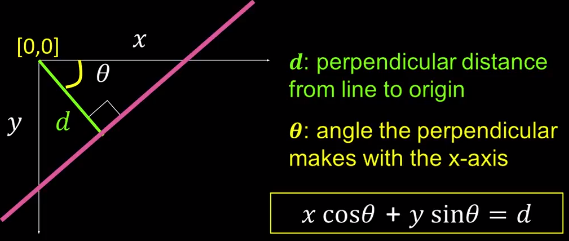
应为 \(x*cos\theta\) - \(y*sin\theta = d\)
d为两个距离的差,图示不对
如果将图像的左上角限定为原点,则\(\theta\)的范围限定在\([0,\pi]\)
- 推导:
算法
- 初始化霍夫空间 \(H[d, \theta] = 0\)
- 投票
for each edge point in (x,y)
for theta = 0 to 180 // 量化
d = x*cos(theta) - y*sin(theta)
H[d, theta] += 1
- 找到霍夫空间中得票数最多的点 \((d, \theta)\) (霍夫峰,Hough Peaks)
- 检测到的线为:\(d = x*cos\theta - y*sin\theta\)
复杂度
- 空间复杂度(需要的内存大小)
- \(k^n\) 个bins (霍夫空间为n维,每个维度需要k个bins)
- 时间复杂度 (投票次数和投票时间)
- 投票次数与边缘点的数量成线性关系
- 投票时间为常数
扩展
- 使用其他参数
- 使用梯度代替角度
- 通过控制点的数量减少投票次数,即减少时间复杂度
- \(\theta = gradient\ at\ (x,y)\)
- \(d = x*cos\theta - y*sin\theta\)
- 使用梯度代替角度
- 越强的边缘点得到的投票越多
- 对不同的分辨率进行采样
- 先对低分辨率(大区间块)进行统计,防止漏掉模型
- 然后用高分辨率(小区间块)进行精确分析
检测圆
圆的方程:
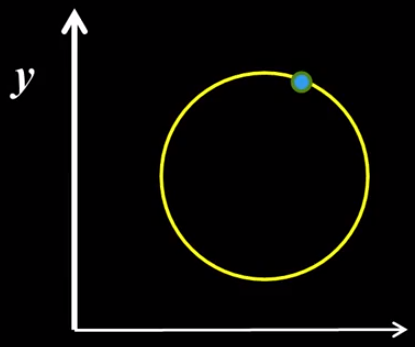
其中的参数有3个,则其霍夫空间是三维的
画圆投票
将圆中的每个点按照一定半径画圆:
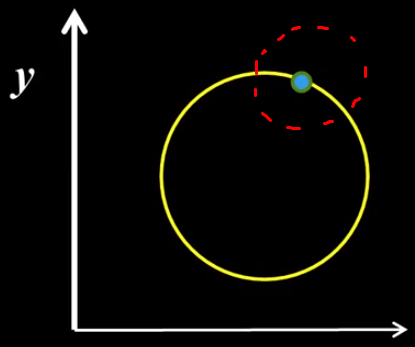
每个圆在霍夫空间中对应一个圆,不同的半径的圆组合起来在霍夫空间中形成一个圆锥:
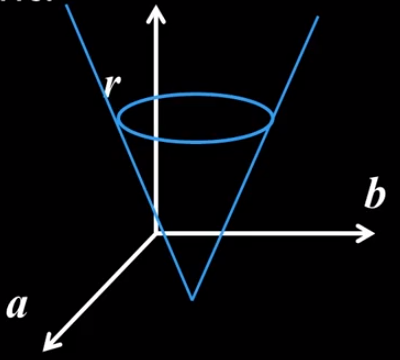
按照梯度投票
在梯度方向上划线,结合上述画圆投票的方法,梯度的线与上述的圆的交点,在霍夫空间中是原来圆锥表面上的一条线
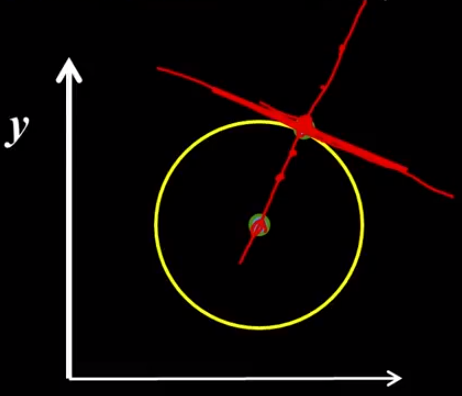
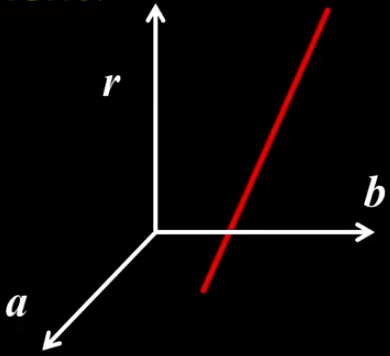
- 算法
for every edge pixel (x,y):
for each possible radius r:
for each possible gradient direction theta:
%%or use estimated gradient
a = x - r*cos(theta)
b = y + r*sin(theta)
H[a,b,r] += 1
end
end
end
技巧及优缺点
霍夫变换是一种比较老的方法,但它能帮助理解如何从图像的像素点抽出特定的特征,一种比较老的方法来理解物体是如何被描述的
技巧
- 尽量减少无关投票的点,比如选择较大量级的梯度上的点
- 选择合适的霍夫空间网格(没有固定标准,根据情况选择)
- 太松散:易获得较大投票点
- 太密集:易丢失投票点,因为同一条线上的边缘点不会精确地共线
- 投票时连同它的相邻网格也投票,相当于在投票结束以后进行了一个平滑化
- 使用边缘点的梯度,相当于降低了霍夫空间一个维度
- 追踪投票到每个网格块的每个点,然后回溯到图像上。比如霍夫空间中对应某个圆的一个点,回溯到图像上,这样能找到属于这个圆并且还未投票的其他边缘点
优缺点
- 优点
- 所有点独立投票,所以能够应对遮挡的情况
- 能够过滤噪音
- 用统一的方法能找到一个模型的多个示例
- 缺点
- 随模型参数的增多,搜索时间的复杂度成指数增加
- 非目标形状会产生伪峰值
- 网格密度难以统一
通用霍夫变换
霍夫表
Hough table 或 R-table
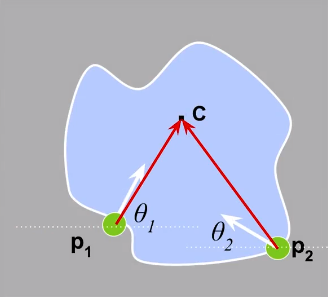
对任意形状,以上图为例,用如下步骤来训练一个霍夫表:
- 首先选取一个中心点 c (比如重心,或用于标记该物体的点)
- 对每个边缘点,计算位移矢量 \(r=c-p_i\)
- 计算每个边缘点的梯度方向 \(\theta\)
- 使用霍夫表保存位移r,用 \(\theta\) 索引之
识别过程:
- 对每个边缘点,计算其梯度方向 \(\theta\)
- 查找霍夫表中由 \(\theta\) 索引的所有位移 r
- 在霍夫空间中,对查找到的所有 r 进行投票
示例
以以下多边形为例
底边上的梯度方向都相同,它索引了一些位移:
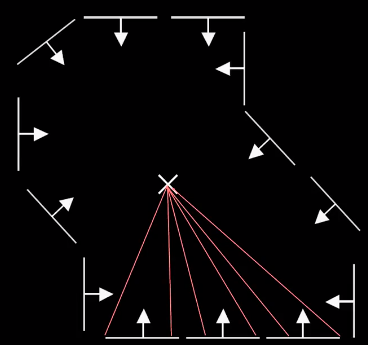
假设图像的梯度图中有匹配的形状,则对底边上某一点对应的梯度方向进行投票:
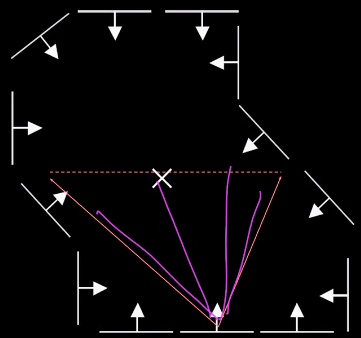
对底边所有点的梯度进行投票:
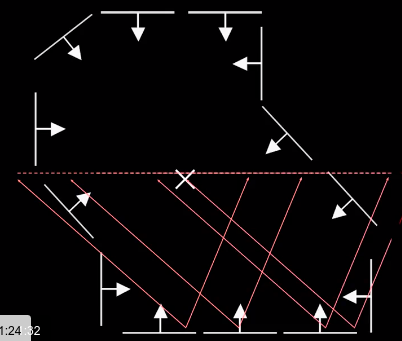
这些投票形成了一条线,靠近中心点的地方投票比较多:

其他 \(\theta\) 的投票:
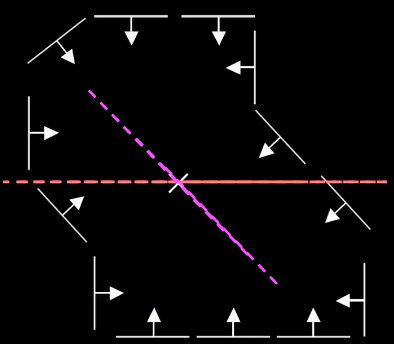
广义情形
有另外两个自由度需要考虑:物体的方向和缩放尺寸。通常情况下,这两者都是未知的。
当物体方向未知时,霍夫空间扩展一个维度,加入方向维度,即由原来的 \((x,y) 扩展为 (\theta^* , x, y, S)\) (S为缩放尺寸 Scale)
缩放尺寸未知时,可以将霍夫空间扩展一个维度,加入尺寸维度,即由原来的 \((\theta^* , x,y) 扩展为 (\theta^* , x, y, S)\) (S为缩放尺寸 Scale)
也可以使用“可视码字” (visual codeword)代替梯度方向,来索引位移:

具体做法是将魔板图片中的特征点(小切图,标签)作为索引,将他们与位移关联:

使用车轮标签进行投票:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号