HCIA-AI v2.0 培训07: 深度学习概览

深度学习概览

• 内容

描述神经网络的定义与发展

区分不同的神经网络

熟悉神经网络的训练与优化

了解深度学习的常见应用

目录

• 深度学习概览
  • 神经网络的定义与发展
    • 典型的机器学习步骤
    • 特征对学习的影响
    • ML vs. DL
    • 神经网络
  • 深度学习的训练法则
    • 梯度下降法与损失函数
    • 常用损失函数
    • 全局梯度下降算法（BGD）
    • 随机梯度下降（SGD）
    • 小批量梯度下降（MBGD）
    • 反向传播算法
  • 激活函数
  • 神经网络的类型
    • 前馈神经网络
    • 卷积神经网络
      • 核心思想
      • 池化层
      • 全连接层
    • 循环神经网络
      • 时序反向传播（BPTT）
      • RNN类型
      • 标准RNN结构的问题
      • 标准LSTM结构
    • 生成式对抗神经网络（GAN）
      • 生成模型与判别模型
      • GAN训练法则
      • 应用
  • 深度学习中的正则化
    • 防止过拟合
    • 参数惩罚
    • 数据集扩充
    • Dropout
    • 提前停止训练
  • 优化器
    • 动量优化器
    • Adagrad优化器
    • RMSprop优化器
    • Adam优化器
  • 深度学习的应用

神经网络的定义与发展

典型的机器学习步骤

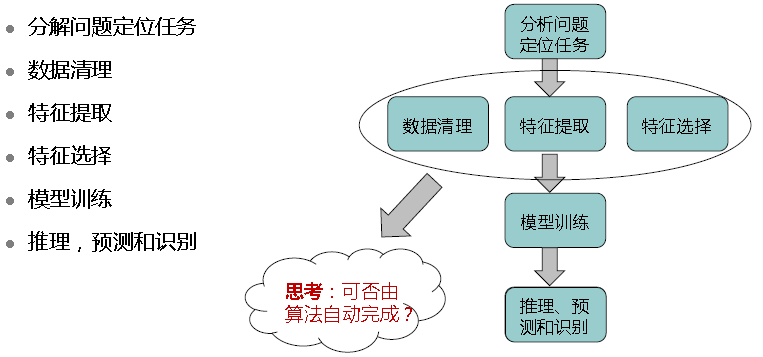
特征对学习的影响

• 一般来说，机器学习中特征是由人工选定，而特征越多，给出的信息就越多，识别准确率会得到提升
• 但特征多，计算复杂度增加，搜索空间大，训练数据会在全体特征向量中会显得系数，影响相似性判断，即维度爆炸
• 更重要的的是，对分类无益的特征，反而会干扰学习效果
• 结论：特征不一定越多越好， 获得好的特征是识别成功的关键。需要多少个特征，可以由学习问题本身来决定。

ML vs. DL

深度学习是一种基于无监督特征学习和特征层次结构的学习模型

神经网络

神经网络：由多个非常简单的处理单元彼此按某种方式相互连接而成的计算机系统，该系统靠其状态对外部输入信息的动态响应来处理信息（美国神经网络学家 Hecht Nielsen 的观点）

人工神经网络是一种旨在模仿人脑结构机器功能的信息处理系统。是从微观结构和功能上对人脑的抽象、简化，是模拟人类智能的一条重要途径，反映了人脑功能的若干基本特征，如并行信息处理、学习、联想、模式分类、记忆等。

• 里程碑:

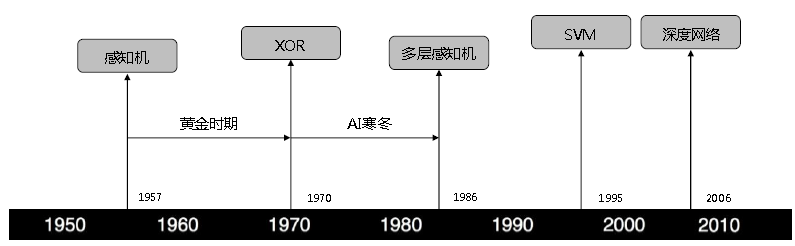
单层感知器：无法解决异或问题

多层感知器（前馈神经网络）：可解决异或问题

深度学习的训练法则

梯度下降法与损失函数

对损失函数求梯度，使参数沿着损失函数的梯度下降最快的方向移动，以完成损失函数最小化

• 优点
  • 只需要求解损失函数的一阶单数，计算代价小，可以在很多大规模数据集上应用
• 缺点
  • 求解的是局部最优值
  • 受步长影响，太小收敛速度慢，太大找不到最优解甚至导致震荡

常用损失函数

• 均方误差
• 交叉熵误差

交叉熵刻画了两个概率分布之间的距离，是分类问题中使用较多的一种损失函数

均方误差多用于回归问题，交叉熵误差多用于分类问题

全局梯度下降算法（BGD）

使用全部样本计算梯度，收敛过程非常慢，并不常用

随机梯度下降（SGD）

有两种叫法：增量梯度下降（Incremental Gradient Descent）和随机梯度下降（Stochastic Gradient Descent）。其中一种实现称为在线学习，它根据每个样本来更新梯度

• 优点
  • 计算速度快
• 缺点
  • 收敛性能不好

小批量梯度下降（MBGD）

把数据分为若干批次，按批次来更新参数，这样一个批次的数据共同决定了本次梯度的方向，下降时不容易跑偏，减少了随机性，提高了收敛性能

优点：减少了计算开销，降低了随机性

反向传播算法

激活函数

引入非线性因素

• sigmoid函数

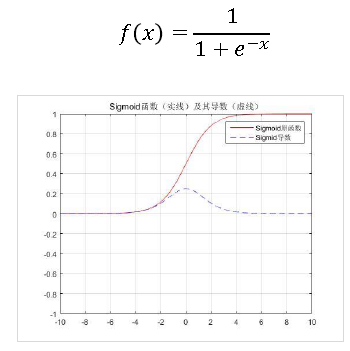
• tanh函数

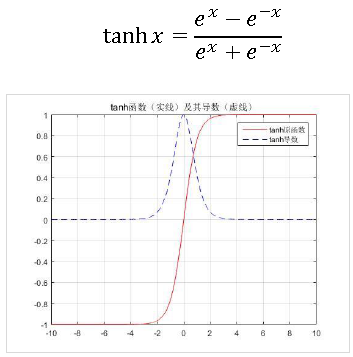
• Softsign 函数

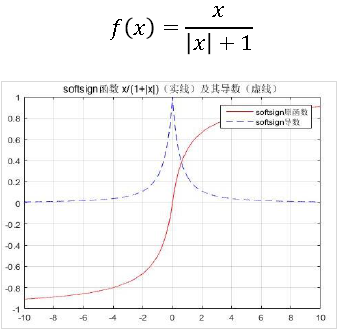
• 梯度消失问题

在远离函数中心点的位置，函数导数趋于零，在网络非常深的时候，越来越多反向传播的梯度会落入饱和区，让梯度的模越来越小，最终趋于零，权重无法更新

一般来说，层数超过5层，就会产生梯度退化为0的现象

• ReLU函数

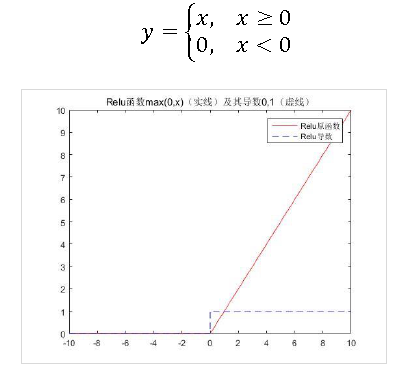
优点：减少了计算量（线性函数求导快，计算量小）；有效减缓了梯度消失问题（没有饱和区）

• Softplus函数

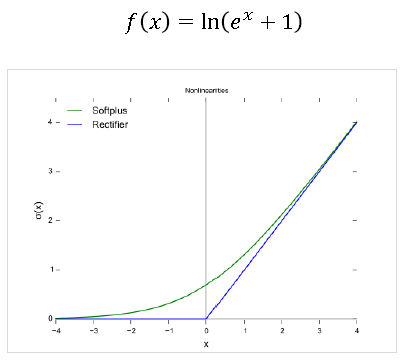
• Softmax函数

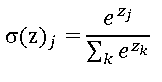
Softmax函数的功能是将一个K维的任意实数向量映射成另一个K维的实数向量，其中向量中每个元素取值都介于(0,1)之间。新向量所有维度模长之和为1

Softmax函数常用来做多分类任务的输出层

神经网络的类型

前馈神经网络

没有反向传播，只有推理过程

卷积神经网络

一种前馈神经网络，用于图像处理，包括卷积层、池化层和全连接层

核心思想

• 局部感知

人对外界的认知是从局部到全局的，而图像的空间联系也是局部的像素联系紧密，距离较远的像素相关性较弱。因此，每个神经元没必要对全局图像进行感知，只需要对局部进行感知，然后再更高层将局部的信息综合起来就得到全局信息。

• 参数共享

卷积核在遍历整个图像的时候，卷积核的参数是不变的，即在同一次卷积时所有像素共享卷积核参数

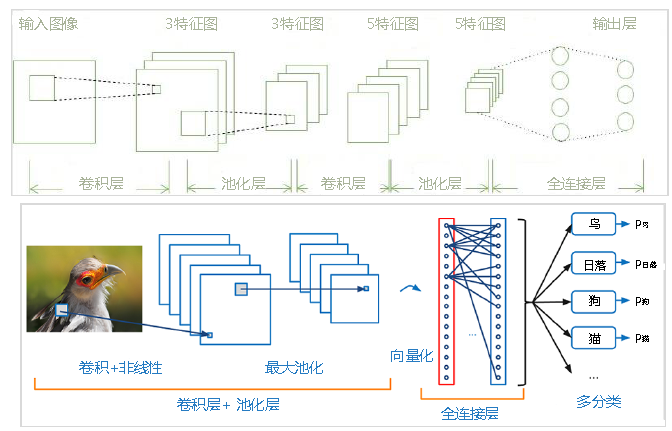
池化层

包括最大池化和平均池化（average pooling）

起到降维的作用，保证目标物体的平移不变性

全连接层

其实是个分类器，将卷积层和池化层提取的特征拉直后放到全连接层中，输出即分类

通常用Softmax作为输出层的激活函数，把所有局部特征结合变成全局特征

循环神经网络

Recurrent neural network

一种通过隐藏层节点周期性的连接，捕捉序列化数据中动态信息的神经网络，可以对序列化的数据进行分类

与其他NN不同，RNN可以保存一种上下文的状态，甚至能在任意长的上下文窗口中存储、学习、表达相关信息，而且不再局限于传统神经网络再空间上的边界，可以再时间序列上有延拓，即在本时间的隐藏层和下一时刻的隐藏层之间的节点间有边。

RNN广泛应用在和序列有关的场景中，如一帧帧的图像组成的视频，一个个片段组成的音频，一个个词组成的句子

• 展开：

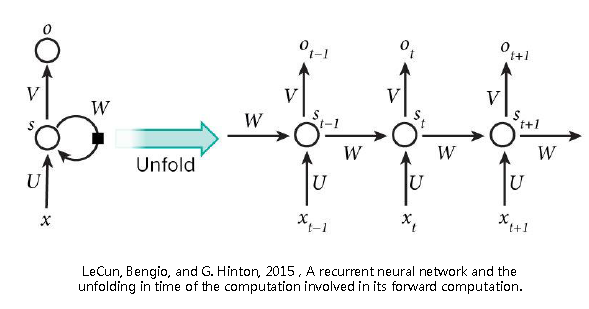
时序反向传播（BPTT）

• 传统反向传播（BP）在时间序列上的拓展

• t时刻的梯度是前t-1时刻所有梯度的累计

• 时间越长，梯度消失越明显

• 步骤

  • 前向计算每个神经元的输出值
  • 反向计算每个神经元的误差值 \(\delta_j\)
  • 计算每个权重的梯度
  • 使用随机梯度下降算法更新权重

RNN类型

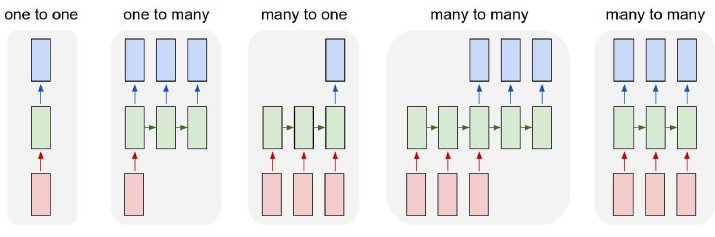
标准RNN结构的问题

\[S_t = \sigma(UX_t + WS_{t-1}) \\ = \sigma(UX_t + W(\sigma(UX_{t-1} + W(...)))) \]

• 标准RNN结构解决了信息记忆的问题，但对于长时间记忆的信息会衰减
• 很多任务需要保存长时间记忆信息
• 在记忆单元容量有限的情况下，RNN会丢失长时间间隔的信息
• 我们希望记忆单元能够选择性记住重点信息

标准LSTM结构

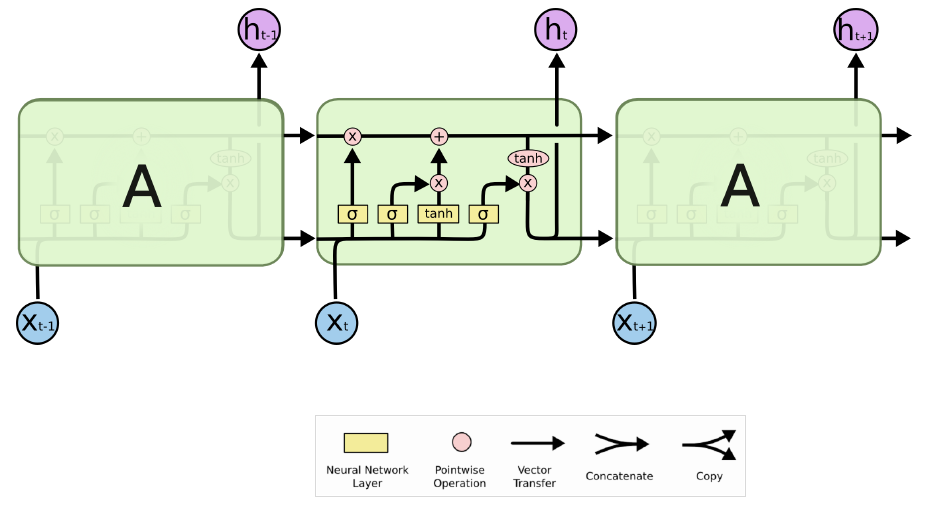
生成式对抗神经网络（GAN）

GAN: Generative Adversarial Nets

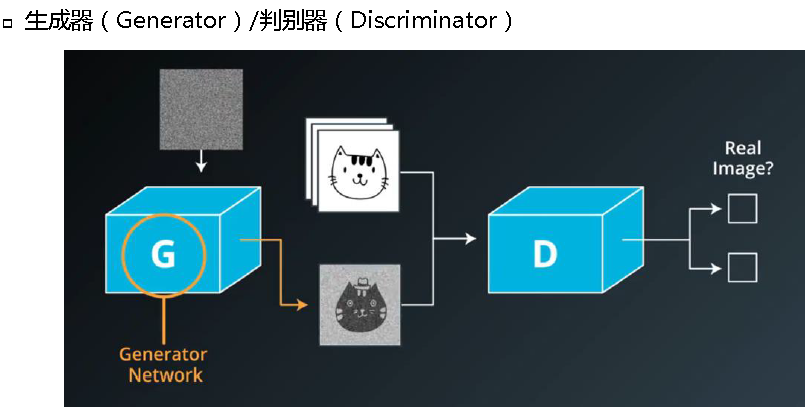
通过对抗过程，通过训练生成器G和判别器D，两者进行博弈，最终使判别器无法区分样本是来自生成器伪造的样本还是真实样本。

生成器（G）：输入“噪声”z（z服从一个人为选取的鲜艳概率分布，如均匀分布、高斯分布等）。采用多层感知机的网络结构，用最大似然估计（MLP）的参数来表示可导映射G(z),将输入空间映射到样本空间

判别器（D）：输入为真实样本x和伪造样本G(z)，并分别带有标签real和fake。判别器网络可以用带有参数的多层感知机。输出为判别样本是否为真实样本数据的概率D(G(z))。

生成模型与判别模型

GAN中，同时存在两种模型：生成模型（Generative Model）和判别模型（Discriminative Model）. 判别模型需要输入变量，通过某种模型来预测分类。生成模型是给定某种隐含信息，来随机产生观测数据

GAN训练法则

• 目标函数

\[\min_G\max_D V(D,G) = E_{x~p_{data}}(x)[\log D(x)] + E_{z~p_{z(z)}}[\log (1 - D(G(z)))] \]

• 训练初期，当G的生成效果很差时，D会以高置信度来判别生成样本为假，因为它们与训练数据明显不同。此时 \(\log(1-D(G(z))\) 饱和（D(G(z))接近0，梯度也近似为0，无法迭代）。因此此时选择最大化 \(\log D(x)\) 而不是最小化 \(\log(1-D(G(z)))\) 来训练G
• 为防止过拟合，在优化D的k个步骤和优化G的1个步骤之间交替更新，只要G变化足够慢，就可以保证D保持在最佳解附近
• 当 \(p_{z(z)} = p_{data}\) 时，达到全局最优（鞍点）

应用

• 图像生成
• 语义分割
• 文字生成
• 数据增强
• 聊天机器人
• 信息检索，排序

深度学习中的正则化

防止过拟合

• 参数约束（范数等）
• 训练集扩充，如添加噪音、数据变换等
• Dropout
• 提前停止

参数惩罚

l1, l2 正则

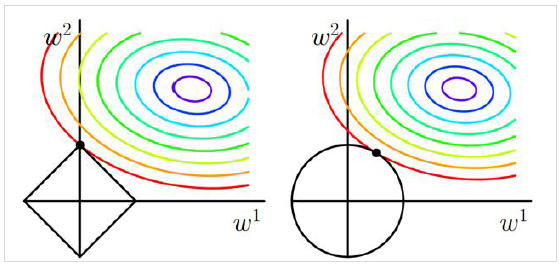
L1 更能产生稀疏的模型，L1正则下，比较小的参数能够直接缩减至0，因此可以起到特征选择的作用

L2范数相当于参数服从高斯先验分布，L1范数相当于拉普拉斯分布

数据集扩充

数据增强：旋转、缩放、随机裁剪、增加噪音、对隐藏层或输出层增加噪音（如softmax分类问题可以通过label smoothing 技术添加噪声）、扭曲；近义词替换

Dropout

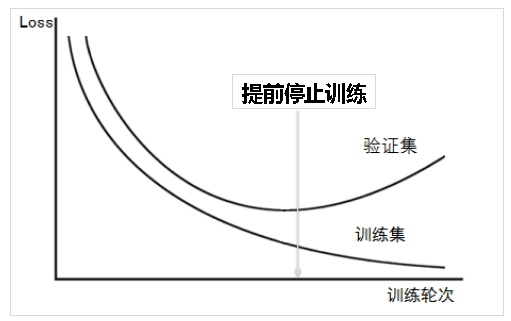
随机丢弃一部分神经元，使其参数不更新。相当于Dropout 是一个集成方法，将所有子网络结果进行合并，通过随机丢弃输入可以得到各种子网络

提前停止训练

优化器

梯度下降算法有许多改进版本。在面向对象语言的实现中，往往把不同的梯度下降算法封装成一个对象，称为优化器

改进的目的有：加快算法收敛速度；尽量避开或冲过局部极值；减少手工参数的设置难度，主要是学习率（LR）

常见的优化器：普通GD优化器、动量优化器、Nesterov、Adagrad、Adadelta、RMSprop、Adam、AdaMax、Nadam

动量优化器

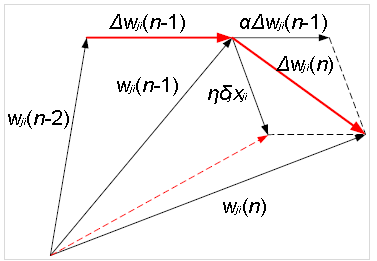
一个最基本的改进，为 \(\Delta w_{ji}\) 增加动量项（保留上一次参数的变化值）

\[\Delta w_{ji}(n) = \eta\delta_jx_{ji} + \alpha \Delta w_{ji}(n-1) \]

\(0\leq\alpha<1\) 是一个常数，称为动量，\(\alpha \Delta w_{ji}(n-1)\) 称为动量项

• 优点
  • 增加梯度修正方向的稳定性，减少突变
  • 在梯度方向稳定的区域，优化速度越来越快（受 \(\alpha\) 影响，有上限），有助于快速穿过平坦区域，加快收敛
  • 由于惯性，可使代价函数快速穿过一些狭窄的局部极值
• 缺点
  • 学习率 \(\eta\) 和动量 \(\alpha\) 仍然需要手动设置，而这往往需要较多的实验来确定合适的值

Adagrad优化器

SGD, MBGD, 动量优化器的共同点是每个参数都用相同的学习率进行更新

Adagrad 的思想是应该为不同的参数设置不同的学习率

刚开始学习率会非常大，随着更新次数增大，学习率越来越慢

• 优点
  • 学习率自动更新，随着更新次数增加，学习率变慢
• 缺点
  • 分母会不断累积，学习率会变小，算法更新变慢

RMSprop优化器

改进的 Adagrad 优化器，通过引入一个衰减系数，让r每回合都衰减一定比例

很好的解决了 Adagrad 优化器过早结束的问题，很适合处理非平稳目标，对RNN网络效果很好

Adam优化器

Adaptive Moment Estimation，是从Adagrad,Adadelta 上发展而来，Adam 为每个待训练变量维护了两个附加的变量 \(m_t 和 v_t\)

\[m_t = \beta_1m_{t-1} + (1-\beta_1)g_t \\ v_t = \beta_2v_{t-1} + (1-\beta_2)g_t^2 \]

\(g_t\) 表示本次计算出的梯度， \(m_t 和 v_t\) 分别是梯度和梯度平方的移动均值。即他们分别是梯度的一阶矩（均值）和二阶矩（方差）的估计

若以0来初始化m和v，在开始迭代时，尤其是 \(\beta_1,\beta_2\) 接近1时，他们非常接近0，为解决这个问题，我们实际上使用的是 \(\hat{m_t} 和 \hat{v_t}\) ：

\[\hat{m_t} = \frac{m_t}{1-\beta_1^t} \\ \hat{v_t} = \frac{v_t}{1-\beta_2^t} \]

权值更新方法：

\[w_{t+1} = w_t - \frac{\eta}{\sqrt{\hat{v_t}} + \epsilon}\hat{m_t} \]

表面上依然需要手动设置 \(\eta, \beta_1, \beta_2\) ，但实际上难度大大降低。根据实验一般取 \(\beta_1=0.9, \beta_2=0.999, \epsilon=10^{-8}, \eta=0.001\) 。Adam在实际应用中会迅速收敛，当收敛到饱和的时候，可适当降低 \(\eta\) ，一般降低几次之后，会收敛到满意的局部极值，其他参数不必调整

深度学习的应用

• 计算机视觉
  • 图像分类
  • 场景识别
  • 人脸检测/识别
  • 物体检测识别
  • 语义分割
  • 风格化
  • 超分辨率
  • OCR
  • 风格迁移
  • 自动上色
• 数据挖掘
• 自然语言处理
  • 中文分词
  • 知识挖掘
  • 机器翻译
  • 情感分析
  • 自动写作
  • 文本摘要
• 语音识别