HCIA-AI v2.0 培训04: AI数学基础

AI数学基础

掌握线性代数的基础知识及应用

掌握概率论的基础知识及应用

掌握优化问题的分类与解决方法

目录

• AI数学基础
  • 数学与AI
  • 线性代数
    • 特殊矩阵
      • 正交矩阵
      • 行列式
    • 矩阵分解
      • 特征分解
      • 奇异值分解（Singular Value Decomposition）
  • 概率论
    • 随机变量及其分布
      • 随机试验
      • 伯努利分布
      • 二项分布
      • 泊松分布
      • 分布函数(连续分布)
      • 正态分布
    • 随机向量及其分布
    • 贝叶斯公式
      • 条件概率也叫后验概率
      • 中文分词
      • 协方差、相关系数、协方差矩阵
  • 最优化问题
    • 最优化问题分类
    • 梯度下降
      • 凸函数
      • 梯度下降法

数学与AI

线性代数、概率论、微积分、统计学

线性代数

神经网络中所有参数都被存储在矩阵中，GPU可以并行处理向量和矩阵运算

• 张量：多维数组
  • 零阶张量：标量；一阶张量：向量；二阶张量：矩阵

特殊矩阵

正交矩阵

满足\(AA^T = A^TA = I_n\),则称A为正交矩阵，即\(A^{-1}=A^T\)

• 深度学习中，常需要求逆矩阵，但由于计算量巨大，因此常将矩阵转成其他特殊矩阵以避免或简化矩阵求逆

• 正交矩阵的行向量之间与列向量之间都是两两正交的单位向量

• n阶正交矩阵可以看做n维空间中任意相互垂直坐标基

• 向量乘以一个正交矩阵：可以看做是对向量只进行旋转，而没有伸缩和空间映射作用

• 正交矩阵的应用：

  • RNN中防止梯度消失和维度爆炸的方法：正交初始化
  • 对于正交矩阵，可将求逆过程转化为矩阵的逆
  • 矩阵分解

行列式

det(A) 或 |A|

• 行列式等于矩阵特征值的乘积
• 行列式的绝对值可用来衡量矩阵参与矩阵乘法后空间扩大或缩小了多少
  • 正交矩阵的行列式大小为1或-1，即用正交矩阵进行线性变换后的矩阵在空间中的有向面积或体积保持不变
• 行列式的正负表示空间的定向
• 行列式的应用：求特征值，求线性方程等

矩阵分解

特征分解

A的特征分解：\(A=P·diag(\lambda)·P^{-1}\)

P为特征向量组成的矩阵

• 从现行空间的角度看，特征值越大，则矩阵在对应的特征向量上的方差越大，信息量越多
• 在最优化中，矩阵特征值的大小与函数值的变化快慢有关，在最大特征值所对应的特征方向上函数变化最大，也就是该方向上的方向导数最大
• 应用：用于降维的PCA、最优化问题、用于处理模型过拟合的正则化

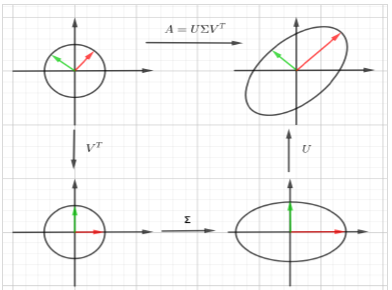
奇异值分解（Singular Value Decomposition）

将矩阵分解为奇异向量和奇异值：\(A_{m,n} = U_{m,m} \Sigma_{m,n} V^T_{n,n}\)

U,V都是正交矩阵，他们的列向量分别叫做左奇异向量和右奇异向量，\(\Sigma\)为对角矩阵（不一定是方阵），对角线上的元素称为矩阵A的奇异值，奇异值按从大到小的序列排列

• 应用：PCA，数据压缩（以图像压缩为代表）算法，特征提取、数字水印和LSI（Latent semantic analysis, 潜在语义分析）

• 几何意义：

  • 在原空间内找到一组正交基\(v_i\)通过矩阵乘法将这组正交基映射到像空间中，其中奇异值对应伸缩系数
  • 奇异值分解将矩阵原本混合在一起的旋转、缩放和投影的三种作用效果分解出来了

• 应用实例 - 图像压缩

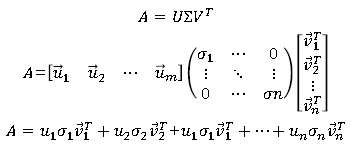
A 是一个m*n 大小的图像，式中奇异值矩阵中奇异值从大到小排列，数值越大，其对应的奇异向量越重要；值越小，越不重要，可以舍去。若只取前k项，即能基本看清图像，则可以达到图像压缩的效果

概率论

• 应用

机器翻译中，确定语言种类

用神经网络进行图像分类，网络的输出是衡量分类结果可信程度的概率值，即分类置信度

混合高斯模型、隐马尔可夫模型等传统语音处理模型

随机变量及其分布

随机试验

• 特点
  • 可以在相同条件下重复进行
  • 每次实验可能结果不止一个，且能事先明确实验所有可能结果
  • 进行一次实验前不能确定哪个结果会出现
• 分布函数：概率质量函数，PMF, Probability Mass Function

伯努利分布

0-1 分布，两点分布，a-b分布

随机变量只取两个值，分布概率为

\[P{x=k} = p^k(1-p)^(1-k), k=0,1(0<p<1) \]

X 服从以p为参数的伯努利分布

• 伯努利分布主要用于二分类问题，可以用伯努利朴素贝叶斯进行文本分类或垃圾邮件分类
• 为防止模型过拟合，常会用dropout方法随机丢弃神经元，每个神经元都被建模为伯努利随机变量，被抛弃的概率为p，成功输出的比例为1-p

二项分布

重复n次伯努利试验满足的分布

n次实验A事件发生k次的概率：

\[P(X=k) = C_n^kp^k(1-p)^{n-k}, k=0,1,2,...,n \]

X服从参数为n，p的二项分布，\(X~B(n,p)\)

期望值与方差为：

\[E(X) = np, Var(x) = np(1-p) \]

• 二项分布在NLP中使用地非常广泛
• Dropout方法中，对某层n个神经元在每个训练步骤中可以被看做是n个伯努利试验的集合，即被丢弃的神经元总数服从参数为n，p的二项分布

泊松分布

随机变量可能的取值为0,1,2,...，取每个值的概率为：

\[P{X=k} = \frac{\lambda^ke^{-\lambda}}{k!}, k=0,1,2,... \]

称X服从泊松分布，记为\(X~P(\lambda)\)，其中 \(E(X) = \lambda, D(X) = \lambda\). \(\lambda\) 是单位时间或单位面积内随机事件的平均发生率

• 泊松分布是二项分布当n很大p很小时的近似计算
• 泊松分布用于描述单位时间内随机事件发生的次数。
  • 如一段时间内某客服电话受到的服务请求次数、汽车展台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数等
• 图像处理中，图像会因为观点显示仪器测量造成的不确定性而出现服从泊松分布的泊松噪声，也可以给图像加泊松噪声用于图像的数据增强

分布函数(连续分布)

• 分布函数：CDF, Cumulative Distribution Function
• 概率密度函数：PDF, Probability Density Function

正态分布

\[f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, -\infty < x < \infty \]

其中 \(\mu, \sigma (\sigma > 0)\) 为常数，称X服从正态分布，记为 \(X~N(\mu, \sigma^2)\)

\(\mu=0, \sigma=1\) 时为标准正态分布

• 图像处理中，可以给图像添加高斯噪声用于图像增强，也可用高斯滤波器去除噪声并平滑图像，还可以用混合高斯模型进行图像的前景目标检测
• 传统语音识别模型 GMM-HMM （高斯混合模型-隐马尔可夫）中，高斯混合模型就是由多个高斯分布混合起来的模型

随机向量及其分布

实际应用中，经常需要对问题用多个变量来描述，把多个随机变量放在一起组成向量，称为多维随机变量或者随机向量

• 比如通过人脸判断人的年龄，可能需要结合多个特征（随机变量），如脸型、脸部纹理、面部斑点、皮肤松弛度、发际线等，将他们结合起来映射为一个实数，即年龄

• 联合分布函数

• 联合概率密度函数

贝叶斯公式

条件概率也叫后验概率

已知原因求解事件发生的概率叫做条件概率

\[P(Y|X) = \frac{P(YX)}{P(X)} \]

P(X) 称为先验概率

• 经常需要在已知事件发生的情况下计算P(X|Y), 即事件已经发生了，再分析原因，此时若还知道先验概率P(X)，则可以利用贝叶斯公式计算：

\[P(X|Y) = \frac{P(XY)}{P(Y)} = \frac{P(Y|X)P(X)}{P(Y)} \]

利用全概率公式，可将其写成

\[P(X_i|Y) = \frac{P(Y|X_i)P(X_i)}{\sum_{i=1}^n{P(Y|X_i)P(X_i)}} \]

• 贝叶斯公式应用：中文分词、统计机器翻译、深度贝叶斯网络等

中文分词

协方差、相关系数、协方差矩阵

• 协方差：某种意义上给出了两个随机变量线性相关性的强度

\[Cov(X, Y) = E[(X-E(X))(Y-E(Y))] \]

• 相关系数：线性相关系数，度量两个变量间的线性关系

\[\rho_{XY} = \frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)}} \]

• 协方差矩阵

\[ C = \bigl(\begin{smallmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{smallmatrix}\bigr) \]

最优化问题

最优化问题分类

• 无约束最优化
  • 直接法：暴力搜索
  • 解析法：梯度下降、牛顿法、拟牛顿法、共轭方向法、共轭梯度法
• 约束优化
  • 在x的某些集合s中找f(x)的最大或最小值，集合s内的点称为可行点
  • 引用拉格朗日乘子(等式约束)或KKT(Kuhn-Kuhn-Tucker)条件（不等式约束）将含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题进行求解
• 等式约束最优化
• 不等式约束最优化

梯度下降

凸函数

函数两点连线在这段区间内函数值的上方（向下凸）

\[f(\lambda x_1 + (1-\lambda)x_2) \leqslant \lambda f(x_1) + (1-\lambda)f(x_2) \]

梯度下降法

临界点或驻点：导数为零的点

梯度：最大的带方向的导数