Machine_Learning_in_Action05 - Logistc regression

Logistic regression

sigmoid 函数和逻辑回归分类器

优化

梯度下降算法

缺失值处理

目录

• Logistic regression
  • 逻辑回归分类和 sigmoid 函数
    • sigmoid 函数
  • 使用最优化方法获得最佳回归参数
    • 梯度上升法
    • 训练算法：使用梯度上升找到最佳参数
    • 分析数据：画出决策边界
    • 训练算法：随机梯度上升
      • 改进
  • 实例：从疝气病预测病马的死亡率
  • 完整代码

• 逻辑回归的一般方法
  • 收集数据
  • 准备：数值型数据用于距离计算。最好是结构化数据
  • 分析
  • 训练：最花费时间的地方，找到一套最优参数来分类
  • 测试
  • 应用

逻辑回归分类和 sigmoid 函数

• 优点： 计算量少，易于实现，知识表示易于解释
• 缺点： 易欠拟合，精度低

sigmoid 函数

\[\sigma(z) = \frac{1}{1 + e^{-z}} \]

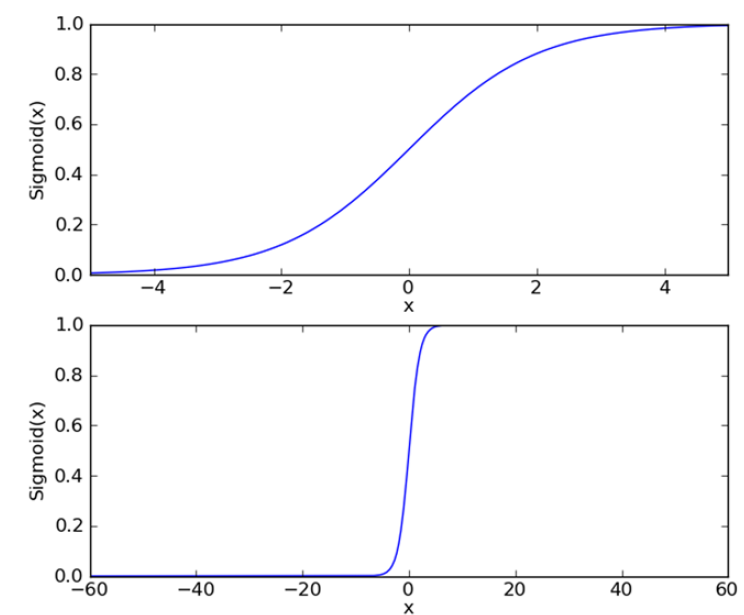
使用最优化方法获得最佳回归参数

梯度上升法

• 梯度

\[ \bigtriangledown{f(x, y)} = \begin{pmatrix} \frac{\partial{f(x,y)}}{\partial{x}} \\ \frac{\partial{f(x,y)}}{\partial{y}} \end{pmatrix} \]

• 更新参数

\[w := w + \alpha\bigtriangledown_{\mathbf{w}}{f(w)} \]

朝着梯度的正方向上升

对于梯度下降方法： \(w := w - \alpha\bigtriangledown_{\mathbf{w}}{f(w)}\)

训练算法：使用梯度上升找到最佳参数

import numpy as np

def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    m,n = np.shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = np.ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose()* error
    return weights

if __name__ == '__main__':
    dataMat,labelMat = loadDataSet()
    weights = gradAscent(dataMat, labelMat)
    print(weights)

分析数据：画出决策边界

def plotBestFit(wei):
    import matplotlib.pyplot as plt
    weights = wei.getA()
    dataMat,labelMat=loadDataSet()
    dataArr = np.array(dataMat)
    n = np.shape(dataArr)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()

• 分类边界

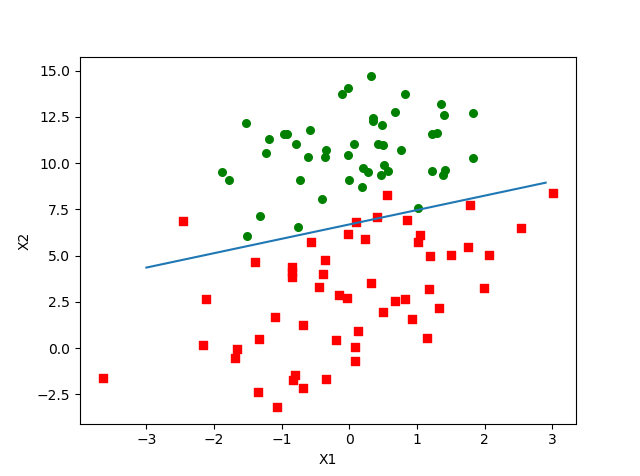
训练算法：随机梯度上升

## stochastic gradient ascent
def stocGradAscent0(dataMatrix, classLabels):
    dataMatrix = np.array(dataMatrix)
    m,n = np.shape(dataMatrix)
    alpha = 0.01
    weights = np.ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    weights = np.mat(weights).transpose()
    return weights

• 分类边界

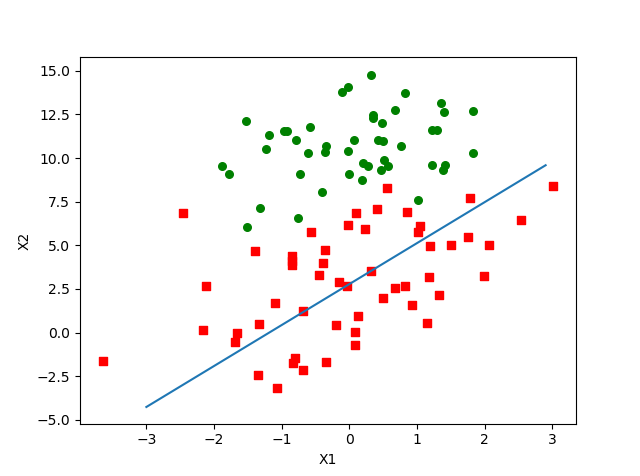
改进

修改学习率

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    dataMatrix = np.array(dataMatrix)
    m,n = np.shape(dataMatrix)
    weights = np.ones(n)
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01
            randIndex = int(random.uniform(0,len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    weights = np.mat(weights).transpose()
    return weights

• 分类边界

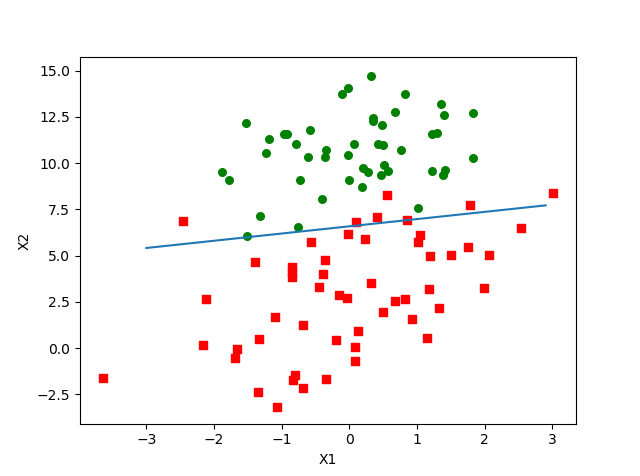
实例：从疝气病预测病马的死亡率

## estimating horse fatalities from colic
def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

def colicTest():
    frTrain = open('horseColicTraining.txt')
    frTest = open('horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(np.array(trainingSet), trainingLabels, 500)
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(np.array(lineArr), trainWeights)) != int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec)
    print("the error rate of this test is: %f" % errorRate)
    return errorRate

def multiTest():
    numTests = 10; errorSum=0.0
    for k in range(numTests):
        errorSum += colicTest()
    print("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)))

---

完整代码

import numpy as np
import random


def loadDataSet():
    dataMat = []; labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    m,n = np.shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = np.ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose()* error
    return weights

def plotBestFit(wei):
    import matplotlib.pyplot as plt
    weights = wei.getA()
    dataMat,labelMat=loadDataSet()
    dataArr = np.array(dataMat)
    n = np.shape(dataArr)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i])== 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()


## stochastic gradient ascent
def stocGradAscent0(dataMatrix, classLabels):
    dataMatrix = np.array(dataMatrix)
    m,n = np.shape(dataMatrix)
    alpha = 0.01
    weights = np.ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    weights = np.mat(weights).transpose()
    return weights

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    dataMatrix = np.array(dataMatrix)
    m,n = np.shape(dataMatrix)
    weights = np.ones(n)
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01
            randIndex = int(random.uniform(0,len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    weights = np.mat(weights).transpose()
    return weights

def ascentTest():
    dataMat,labelMat = loadDataSet()
    # weights = gradAscent(dataMat, labelMat)
    # weights = stocGradAscent0(dataMat, labelMat)
    weights = stocGradAscent1(dataMat, labelMat)
    plotBestFit(weights)

## estimating horse fatalities from colic
def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

def colicTest():
    frTrain = open('horseColicTraining.txt')
    frTest = open('horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(np.array(trainingSet), trainingLabels, 500)
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(np.array(lineArr), trainWeights)) != int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec)
    print("the error rate of this test is: %f" % errorRate)
    return errorRate

def multiTest():
    numTests = 10; errorSum=0.0
    for k in range(numTests):
        errorSum += colicTest()
    print("after %d iterations the average error rate is: %f" % (numTests, errorSum/float(numTests)))


if __name__ == '__main__':
    # ascentTest()
    multiTest()