《Fluid Engine Development》 学习笔记3-光滑粒子流体动力学
用粒子表示流体最热门的方法就是就是光滑粒子流体动力学(Smoothed Particle Hydrodynamics (SPH).)
这种方法模糊了流体的边界,用有限数量的粒子代表流体,该方法的基本思想是将视作连续的流体(或固体)用相互作用的质点组来描述,各个物质点上承载各种物理量,包括质量、速度等,通过求解质点组的动力学方程和跟踪每个质点的运动轨道,求得整个系统的力学行为
经典核函数
SPH算法涉及到“光滑核”的概念,可以这样理解这个概念,粒子的属性都会“扩散”到周围,并且随着距离的增加影响逐渐变小,这种随着距离而衰减的函数被称为“光滑核”函数,最大影响半径为“光滑核半径”。
书中提到的经典核函数有 $W_{std}(r) = \frac{315}{64\pi h^{3}}(1 -\frac{r{2}}{h_{2}}) (0 \leq r \leq h) $,其他情况为0
SPH插值
SPH插值的基本思想是通过查找附近的粒子来测量任意给定位置的任何物理量。它是一个加权平均,权重是质量乘以核函数除以相邻粒子的密度。
质量除以密度就是体积,因此这个插值,将更多的权重放在离原点更近的值上
相关代码实现如下
Vector3D CalfFluidEngine::SphSystemData3::Interpolate(const Vector3D & origin, const std::vector<Vector3D>& values) const
{
Vector3D sum = Vector3D::zero;
auto& d = GetDensities();
SphStandardKernel3 kernel(_kernelRadius);
const double m = GetParticleMass();
GetNeighborSearcher()->ForEachNearbyPoint(
origin, _kernelRadius, [&](size_t i, const Vector3D& neighborPosition)
{
double dist = Vector3D::Distance(origin,neighborPosition);
double weight = m / d[i] * kernel(dist);
sum += weight * values[i];
}
);
return sum;
}
double CalfFluidEngine::SphStandardKernel3::operator()(double distance) const
{
if (distance * distance >= h2) {
return 0.0;
}
else {
double x = 1.0 - distance * distance / h2;
return 315.0 / (64.0 * kPiD * h3) * x * x * x;
}
}
void CalfFluidEngine::PointHashGridSearcher3::ForEachNearbyPoint(const Vector3D & origin, double radius, const std::function<void(size_t, const Vector3D&)>& callback) const
{
if (_buckets.empty()) {
return;
}
size_t nearbyKeys[8];
getNearbyKeys(origin, nearbyKeys);
const double queryRadiusSquared = radius * radius;
for (int i = 0; i < 8; i++) {
const auto& bucket = _buckets[nearbyKeys[i]];
size_t numberOfPointsInBucket = bucket.size();
for (size_t j = 0; j < numberOfPointsInBucket; ++j) {
size_t pointIndex = bucket[j];
double rSquared = (_points[pointIndex] - origin).SquareMagnitude();
if (rSquared <= queryRadiusSquared) {
callback(pointIndex, _points[pointIndex]);
}
}
}
}
我们可以看到插值函数依赖于密度,因为粒子的位置在每个时间步长都会改变,而密度也随之在每个时间步长都会改。
void CalfFluidEngine::SphSystemData3::UpdateDensities()
{
auto& p = GetPositions();
auto& d = GetDensities();
const double m = GetParticleMass();
tbb::parallel_for(
tbb::blocked_range<size_t>(0, GetNumberOfParticles()),
[&](const tbb::blocked_range<size_t> & b) {
for (size_t i = b.begin(); i != b.end(); ++i)
{
double sum = SumOfKernelNearby(p[i]);
d[i] = m * sum;
}
});
}
double CalfFluidEngine::SphSystemData3::SumOfKernelNearby(const Vector3D & origin) const
{
double sum = 0.0;
SphStandardKernel3 kernel(_kernelRadius);
GetNeighborSearcher()->ForEachNearbyPoint(
origin, _kernelRadius, [&](size_t, const Vector3D& neighborPosition) {
double dist = Vector3D::Distance(origin, neighborPosition);
sum += kernel(dist);
});
梯度算子
类似于之前的插值,梯度能用类似的方法获得
Vector3D CalfFluidEngine::SphSystemData3::GradientAt(size_t i, const std::vector<double>& values) const
{
Vector3D sum;
auto& p = GetPositions();
auto& d = GetDensities();
const auto& neighbors = GetNeighborLists()[i];
Vector3D origin = p[i];
SphSpikyKernel3 kernel(_kernelRadius);
const double m = GetParticleMass();
for (size_t j : neighbors) {
Vector3D neighborPosition = p[j];
double dist = Vector3D::Distance(origin, neighborPosition);
if (dist > kEpsilonD) {
Vector3D dir = (neighborPosition - origin) / dist;
sum += m * values[i] / d[j] *
kernel.Gradient(dist, dir);
}
}
return sum;
}
Vector3D ...::Gradient(double distance, const Vector3D & directionToParticle) const
{
return -firstDerivative(distance) * directionToParticle;
}
然而这种梯度的实现是不对称的,相邻的粒子可能会因为拥有不同的价值和密度而拥有不同的梯度,这也意味着2个粒子将被施加不同的力。根据牛顿第三运动定律,每一个作用力都有一个相等且相反的作用力
为解决这个问题,需要修改梯度实现。
书所使用的公式是 \(\nabla \phi(x)= \rho _{j}m \sum_{j}(\frac{\phi_{i}}{\rho _{i} ^{2}} + \frac{\phi_{j}}{\rho _{j} ^{2}}) \nabla W(|x - x_{j}|)\)
Vector3D CalfFluidEngine::SphSystemData3::GradientAt(size_t i, const std::vector<double>& values) const
{
Vector3D sum;
auto& p = GetPositions();
auto& d = GetDensities();
const auto& neighbors = GetNeighborLists()[i];
Vector3D origin = p[i];
SphSpikyKernel3 kernel(_kernelRadius);
const double m = GetParticleMass();
for (size_t j : neighbors) {
Vector3D neighborPosition = p[j];
double dist = Vector3D::Distance(origin, neighborPosition);
if (dist > kEpsilonD) {
Vector3D dir = (neighborPosition - origin) / dist;
sum += d[i] * m *
(values[i] / (d[i] * d[i]) + values[j] / (d[j] * d[j])) *
kernel.Gradient(dist, dir);
}
}
return sum;
}
拉普拉斯算子
类似于之前的插值,按照拉普拉斯的数学定义,尝试计算拉普拉斯算子,结果如下
double CalfFluidEngine::SphSystemData3::LaplacianAt(size_t i, const std::vector<double>& values) const
{
double sum = 0.0;
auto& p = GetPositions();
auto& d = GetDensities();
const auto& neighbors = GetNeighborLists()[i];
Vector3D origin = p[i];
SphSpikyKernel3 kernel(_kernelRadius);
const double m = GetParticleMass();
for (size_t j : neighbors) {
Vector3D neighborPosition = p[j];
double dist = Vector3D::Distance(origin, neighborPosition);
sum += m * values[j] / d[j] * kernel.Laplacian(dist);
}
return sum;
}
double ...::Laplacian(double distance) const
{
return secondDerivative(distance);
}
遗憾的是这般计算拉普拉斯算子在即便所有场值都是相同的非零值时,也不会输出零场
拉普拉斯正确的计算方法如下 \(\nabla^{2} \phi(x)=m \sum_{j}(\frac{\phi_{j} - \phi_{i}}{\rho _{j} } ) \nabla^{2} W(|x - x_{j}|)\)
double CalfFluidEngine::SphSystemData3::LaplacianAt(size_t i, const std::vector<double>& values) const
{
double sum = 0.0;
auto& p = GetPositions();
auto& d = GetDensities();
const auto& neighbors = GetNeighborLists()[i];
Vector3D origin = p[i];
SphSpikyKernel3 kernel(_kernelRadius);
const double m = GetParticleMass();
for (size_t j : neighbors) {
Vector3D neighborPosition = p[j];
double dist = Vector3D::Distance(origin, neighborPosition);
sum += m * (values[j] - values[i]) / d[j] * kernel.Laplacian(dist);
}
return sum;
}
Spiky核函数
梯度算子是用来计算压力梯度的,粒子太接近,压力就会把粒子推开,然而经典核函数即使粒子越来越接近,也会出现压力越来越小的情况,甚至还会出现负值
如下图是原书中的图,a是经典核函数,实线是原核函数,虚线是一阶偏导,点线是二阶导
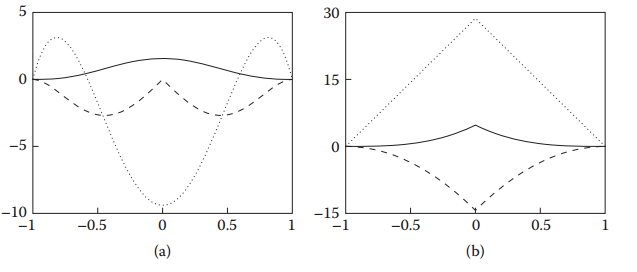
为解决这个问题,Spiky核函数诞生了,如上图b
公式为$W_{spiky}(r) = \frac{15}{\pi h^{3}}(1 -\frac{r{3}}{h_{3}}) (0 \leq r \leq h) $其他情况为0
我们插值获取权重时使用经典核函数,计算拉普拉斯算子和梯度时使用Spiky核函数
主体代码结构
这里给出SPH系统的头文件
class SphSystemSolver3 : public ParticleSystemSolver3
{
public:
SphSystemSolver3();
virtual ~SphSystemSolver3();
void SetViscosityCoefficient(
double newViscosityCoefficient) {
_viscosityCoefficient = std::max(newViscosityCoefficient, 0.0);
}
void SetPseudoViscosityCoefficient(
double newPseudoViscosityCoefficient) {
_pseudoViscosityCoefficient
= std::max(newPseudoViscosityCoefficient, 0.0);
}
void SetTimeStepLimitScale(double newScale) {
_timeStepLimitScale = std::max(newScale, 0.0);
}
std::shared_ptr<SphSystemData3> GetSphData() const;
protected:
virtual void accumulateForces(double timeIntervalInSeconds) override;
virtual void onTimeStepStart(double timeStepInSeconds) override;
virtual void onTimeStepEnd(double timeStepInSeconds) override;
virtual unsigned int getNumberOfSubTimeSteps(
double timeIntervalInSeconds) const override;
private:
void accumulateViscosityForce();
void accumulatePressureForce(double timeStepInSeconds);
void computePressure();
void accumulatePressureForce(
const std::vector<Vector3D>& positions,
const std::vector<double>& densities,
const std::vector<double>& pressures,
std::vector<Vector3D>& pressureForces);
void computePseudoViscosity(double timeStepInSeconds);
//! Exponent component of equation - of - state(or Tait's equation).
double _eosExponent = 7.0;
//! Speed of sound in medium to determin the stiffness of the system.
//! Ideally, it should be the actual speed of sound in the fluid, but in
//! practice, use lower value to trace-off performance and compressibility.
double _speedOfSound = 100.0;
//! Negative pressure scaling factor.
//! Zero means clamping. One means do nothing.
double _negativePressureScale = 0.0;
double _viscosityCoefficient = 0.01;
//Scales the max allowed time-step.
double _timeStepLimitScale = 1.0;
//! Pseudo-viscosity coefficient velocity filtering.
//! This is a minimum "safety-net" for SPH solver which is quite
//! sensitive to the parameters.
double _pseudoViscosityCoefficient = 10.0;
};
SPH系统相比正常的粒子动画系统,重写了accumulateForces函数和onTimeStepStart函数以及onTimeStepEnd函数,分别用以添加粘度压力计算,更新密度,抑制噪声
以下是accumulateForces函数的代码结构
void CalfFluidEngine::SphSystemSolver3::accumulateForces(double timeIntervalInSeconds)
{
ParticleSystemSolver3::accumulateForces(timeIntervalInSeconds);
accumulateViscosityForce();
accumulatePressureForce(timeIntervalInSeconds);
}
可以看到了相比粒子动画,多了粘度和压力的计算
以下是onTimeStepStart函数,用以更新粒子集合的密度
void CalfFluidEngine::SphSystemSolver3::onTimeStepStart(double timeStepInSeconds)
{
auto particles = GetSphData();
particles->BuildNeighborSearcher(particles->GetKernelRadius());
particles->BuildNeighborLists(particles->GetKernelRadius());
particles->UpdateDensities();
}
以下是onTimeStepEnd函数
void CalfFluidEngine::SphSystemSolver3::onTimeStepEnd(double timeStepInSeconds)
{
computePseudoViscosity(timeStepInSeconds);
}
计算压强
状态方程(Equation-of-State ,EOS)描述了状态变量间的关系,我们通过状态方程 \(p = \frac{\kappa}{\gamma}( \frac{\rho}{\rho_{0}}- 1)^{\gamma}\) 将密度映射为压强
inline double computePressureFromEos(
double density,
double targetDensity,
double eosScale,
double eosExponent,
double negativePressureScale) {
// Equation of state
// (http://www.ifi.uzh.ch/vmml/publications/pcisph/pcisph.pdf)
double p = eosScale / eosExponent
* (std::pow((density / targetDensity), eosExponent) - 1.0);
return p;
}
观察上公式,我们发现density 小于 targetDensity会出现负压强的情况,而液体表面附近的确会出现密度过小的情况
为防止负压强的引入,我们需要夹紧压强,具体如下
inline double computePressureFromEos(
double density,
double targetDensity,
double eosScale,
double eosExponent,
double negativePressureScale) {
// Equation of state
// (http://www.ifi.uzh.ch/vmml/publications/pcisph/pcisph.pdf)
double p = eosScale / eosExponent
* (std::pow((density / targetDensity), eosExponent) - 1.0);
// Negative pressure scaling
if (p < 0) {
p *= negativePressureScale;
}
return p;
}
压强计算代码如下
void CalfFluidEngine::SphSystemSolver3::computePressure()
{
auto particles = GetSphData();
size_t numberOfParticles = particles->GetNumberOfParticles();
auto& d = particles->GetDensities();
auto& p = particles->GetPressures();
// See Equation 9 from
// http://cg.informatik.uni-freiburg.de/publications/2007_SCA_SPH.pdf
const double targetDensity = particles->GetDensity();
const double eosScale
= targetDensity * (_speedOfSound * _speedOfSound) / _eosExponent;
tbb::parallel_for(
tbb::blocked_range<size_t>(0, numberOfParticles),
[&](const tbb::blocked_range<size_t> & b) {
for (size_t i = b.begin(); i != b.end(); ++i)
{
p[i] = computePressureFromEos(
d[i],
targetDensity,
eosScale,
_eosExponent,
_negativePressureScale);
}
});
}
这里注意到eosScale参数的计算,并不是我们想象中那样随便取个值,需要通过公式 $\kappa =\rho_{0} \frac{c_{s}}{\gamma} $ cs是流体中的声速,实践中可以用较低的值跟踪性能。
计算压力
\(f_{p} = - m \frac{\nabla p}{\rho}\)
回忆我们之前提到的梯度算子计算方法,我们可以得到\(f_{p}= m^{2} \sum_{j}(\frac{p_{i}}{\rho _{i} ^{2}} + \frac{p_{j}}{\rho _{j} ^{2}}) \nabla W(|x - x_{j}|)\)
void CalfFluidEngine::SphSystemSolver3::accumulatePressureForce(const std::vector<Vector3D>& positions, const std::vector<double>& densities, const std::vector<double>& pressures, std::vector<Vector3D>& pressureForces)
{
auto particles = GetSphData();
size_t numberOfParticles = particles->GetNumberOfParticles();
double mass = particles->GetParticleMass();
const double massSquared = mass * mass;
const SphSpikyKernel3 kernel(particles->GetKernelRadius());
tbb::parallel_for(
tbb::blocked_range<size_t>(0, numberOfParticles),
[&](const tbb::blocked_range<size_t> & b) {
for (size_t i = b.begin(); i != b.end(); ++i)
{
const auto& neighbors = particles->GetNeighborLists()[i];
for (size_t j : neighbors) {
double dist = Vector3D::Distance(positions[i], positions[j]);
if (dist > kEpsilonD) {
Vector3D dir = (positions[j] - positions[i]) / dist;
pressureForces[i] -= massSquared
* (pressures[i] / (densities[i] * densities[i])
+ pressures[j] / (densities[j] * densities[j]))
* kernel.Gradient(dist, dir);
}
}
}
});
}
计算粘度
粘度力公式为\(f_{v} = - m \mu \nabla^{2}u\) 代入之前拉普拉斯算子的计算方法,可得公式\(\nabla^{2} \phi(x)=m^{2} \mu\sum_{j}(\frac{u_{j} - u_{i}}{\rho _{j} } ) \nabla^{2} W(|x - x_{j}|)\)
代码实现如下
void CalfFluidEngine::SphSystemSolver3::accumulateViscosityForce()
{
auto particles = GetSphData();
size_t numberOfParticles = particles->GetNumberOfParticles();
auto& x = particles->GetPositions();
auto& v = particles->GetVelocities();
auto& d = particles->GetDensities();
auto& f = particles->GetForces();
double mass = particles->GetParticleMass();
const double massSquared = mass * mass;
const SphSpikyKernel3 kernel(particles->GetKernelRadius());
tbb::parallel_for(
tbb::blocked_range<size_t>(0, numberOfParticles),
[&](const tbb::blocked_range<size_t> & b) {
for (size_t i = b.begin(); i != b.end(); ++i)
{
const auto& neighbors = particles->GetNeighborLists()[i];
for (size_t j : neighbors) {
double dist = Vector3D::Distance(x[i],x[j]);
f[i] += _viscosityCoefficient * massSquared
* (v[j] - v[i]) / d[j]
* kernel.Laplacian(dist);
}
}
});
}
降低噪声
降低噪声的方法很简单,以参数_pseudoViscosityCoefficient线性插值速度场和加权平均速度即可
void CalfFluidEngine::SphSystemSolver3::computePseudoViscosity(double timeStepInSeconds)
{
auto particles = GetSphData();
size_t numberOfParticles = particles->GetNumberOfParticles();
auto& x = particles->GetPositions();
auto& v = particles->GetVelocities();
auto& d = particles->GetDensities();
const double mass = particles->GetParticleMass();
const SphSpikyKernel3 kernel(particles->GetKernelRadius());
std::vector<Vector3D> smoothedVelocities(numberOfParticles);
tbb::parallel_for(
tbb::blocked_range<size_t>(0, numberOfParticles),
[&](const tbb::blocked_range<size_t> & b) {
for (size_t i = b.begin(); i != b.end(); ++i)
{
double weightSum = 0.0;
Vector3D smoothedVelocity;
const auto& neighbors = particles->GetNeighborLists()[i];
for (size_t j : neighbors) {
double dist = Vector3D::Distance(x[i],x[j]);
double wj = mass / d[j] * kernel(dist);
weightSum += wj;
smoothedVelocity += wj * v[j];
}
double wi = mass / d[i];
weightSum += wi;
smoothedVelocity += wi * v[i];
if (weightSum > 0.0) {
smoothedVelocity /= weightSum;
}
smoothedVelocities[i] = smoothedVelocity;
}
});
double factor = timeStepInSeconds * _pseudoViscosityCoefficient;
factor = Clamp(factor, 0.0, 1.0);
tbb::parallel_for(
tbb::blocked_range<size_t>(0, numberOfParticles),
[&](const tbb::blocked_range<size_t> & b) {
for (size_t i = b.begin(); i != b.end(); ++i)
{
v[i] = Lerp(
v[i], smoothedVelocities[i], factor);
}
});
}
声速参数和时间步长
之前我们计算压强时使用了声速cs,为什么会有声速呢,因为在一个时间步长内,压力传播不能大于粒子核半径h,而水中传播的最快速度就是声速,所以时间步长的理想步长是h/cs
最后,根据几位科学家的研究成果,时间步长需要做如下的限制
\(\Delta t _{v} =\frac{ \lambda _{v} h}{c_{s}} ,\Delta t_{f} = \lambda_{f}\sqrt{\frac{hm}{F_{Max}}}, \Delta \leq(\Delta t_{v},\Delta t_{f})\)
\(\lambda_{v},\lambda_{f}\)是2个预设好的标量,大概0.25~0.4之间,\(F_{max}\) 是力向量的最大大小
然后时间步长因为这种限制可能会非常小,导致巨大的计算成本,而且实际上我们也无法评估最大速度和最大力是多少
为从根本解决这个问题,Solenthaler 和Pajarola提出一种预测-校正模型,消除了对声速的依赖。这个新的模型将在下一篇笔记中阐述。
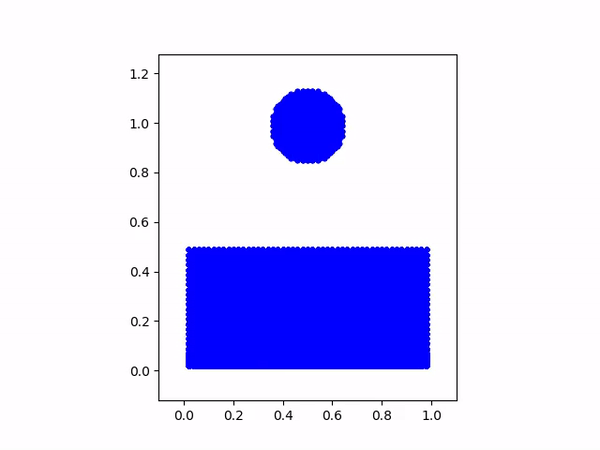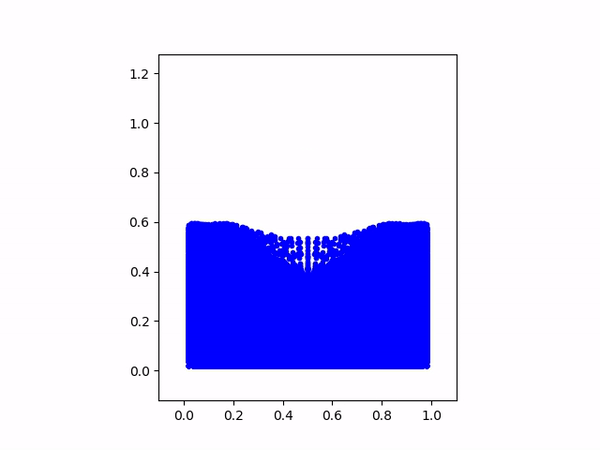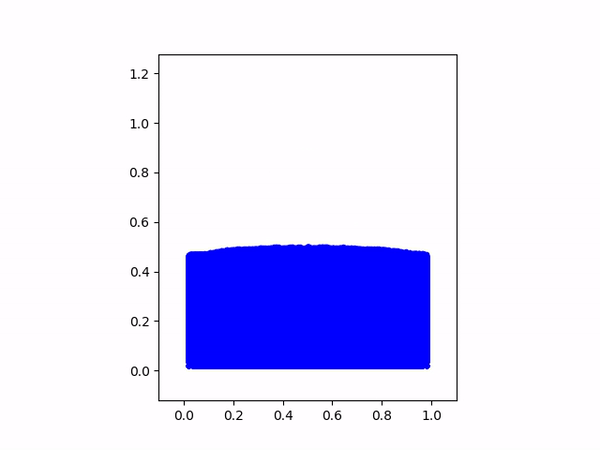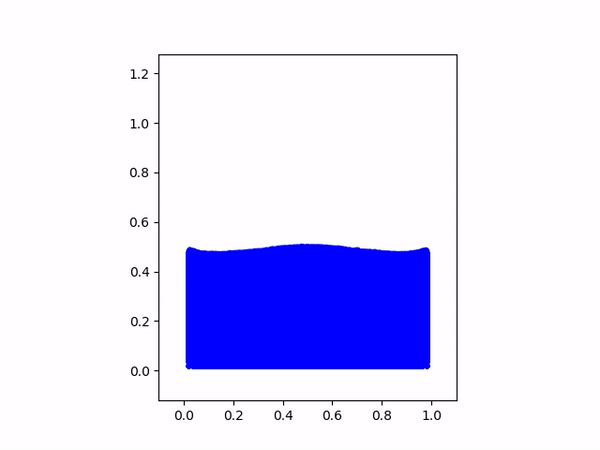
演示模拟结果


 浙公网安备 33010602011771号
浙公网安备 33010602011771号