矩阵快速幂+矩阵乘法

板子：斐波那契数列

今天蒟蒻来学习一个新的东西-矩阵乘法+快速幂

矩阵乘法

\(设A为一个n\times m的矩阵，B为m\times p的矩阵，那么他们的乘积就得到了一个新的矩阵C,其中C的第i行第j列为：\)

\[C_{i,j}=\sum_{k=1}^{m}A_{i,k}B_{k,j} \]

---

得到了这个之后我们再来看题：
\(因为n特别大，所以我们不能直接用递归，保证TLE，那么我们在来用矩阵\)

\[[F[n],F[n-1]]可以由矩阵[F[n-1],F[n-2]]\times{\begin{matrix} 1 1\\ 1 0\end{matrix}}得到 \]

那么我们来推一般式设刚才的矩阵为\(base\)，那么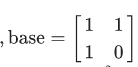
可得：

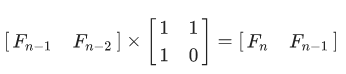
设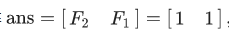
那么\(F_n=\)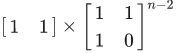

注意矩阵乘法不满足交换律，所以不能交换

---

代码实现：

#include<bits/stdc++.h>
using namespace std;
#define MOD 1000000007
long long n;
long long a[2][2]={{0,1},{1,1}},A[2][2];
long long f[2]={0,1},F[2];
void solve1(){
	memset(F,0,sizeof(F));
	for(int i=0;i<2;i++)
	  	for(int k=0;k<2;k++)
	 		F[i]=(F[i]+f[k]*a[k][i])%MOD;
	memcpy(f,F,sizeof(F));
	return;
}
void solve2(){
	memset(A,0,sizeof(A));
	for(int i=0;i<2;i++)
	 	for(int j=0;j<2;j++)
	 	 	for(int k=0;k<2;k++)
	 	 	 	A[i][j]=(A[i][j]+a[i][k]*a[k][j])%MOD;
	memcpy(a,A,sizeof(A));
	return;
}
int main(){
	scanf("%lld",&n); 
	while(n){
		if(n&1) solve1();
		solve2();
		n>>=1;
	}
	cout<<f[0]%MOD<<"\n";
	return 0;
}