Two point

利用问题的本身与序列的特新，使用两个下标i, j对序列进行扫描（可以同向扫描，也可以反向扫描），以较低的时间复杂度解决问题，一般是O(n)

例1：给定一个递增的正整数序列和一个正整数M，求序列中的两个不同位置的数a和b，使得它们的和恰好为M，输出所有满足条件的方案。加入给定序列{ 1,2,3,4,5,6 }与正整数M = 8，就存在2 + 6 = 8与3 + 5 = 8成立。

暴力解法：时间复杂度为O(n ^ 2)，两层两串层循环枚举。

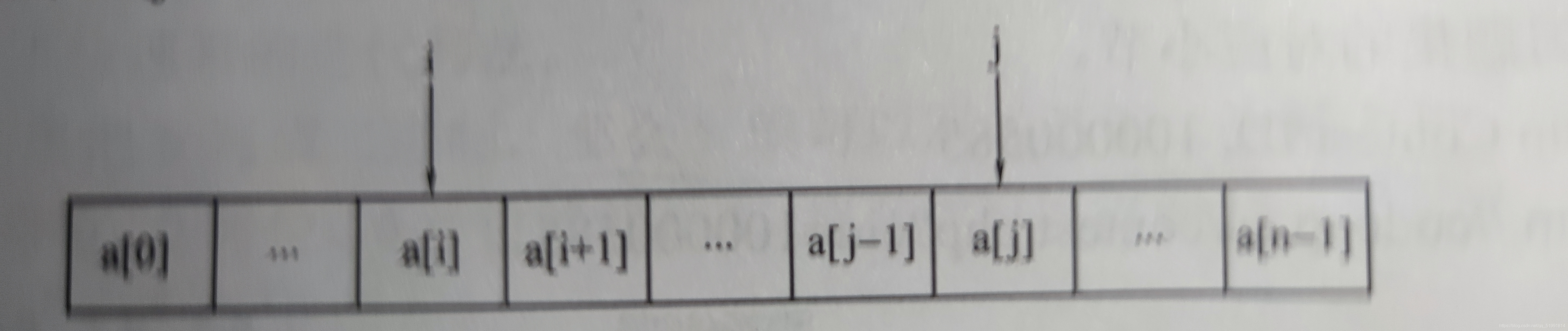
分析：
令下标i的初值为0，下标j的初值为n-1，前者向右移动，后者向左移动，一直到i>=j成立
1.当a[i]+a[j]==M符合条件时，剩余的方案只有可能在[i+1,j-1]中出现于是令i++;j–;
2.当a[i]+[j]<M时，剩余的方案只可能在[i+1,j]中出现，于是让i++;
3.当a[i]+a[j]>M时，剩余的方案只可能在[i,j-1]中出现，j–;
代码实现如下：

while (i >= j) {
    if (a[i] + a[j] == M) {
        i++;
        j--;
    }
    else if (a[i] + [j] < M) {
        i++;
    }
    else j--;
}

此算法的复杂度仅为O(n).

例2：两个递增序列A，B合并成为一个递增序列C，同时考虑两个序列，对两个序列进行比较，再选择填入序列C
代码实现：

int merge(int A[], int B[], int C[], int n, int m) {//n为A[]中元素个数，m为B[]中元素个数。
    int i = 0, j = 0, index = 0;
    while (i < n && j < m) {
        if (A[i] <= B[j]) {
            C[index++] = A[i++];
        }
        else if{
            C[index++] = B[j++];    
        }
        while (i < n){
            C[index++] = A[i++];
        }
        while (j < m){
            C[index++] = B[j++];
        }
        return index;
    }
}