数位dp之记忆化搜索
数位dp之记忆化搜索
前言
数位dp主要解决 “在区间 [l , r] 这个范围内,满足某种 约束 的数字的 数量、总和、平方 ” 的这类问题
针对这种问题,有两种写法:记忆化搜索 和 迭代写法
这里我们采用记忆化搜索的写法,因为好写、思路较为清晰
引入
数位dp有个通用套路:将求解 [l,r] 区间内的满足约束的数的数量转化为求解 \(1 \sim n\) 的满足约束的个数 \(f(n)\) ,然后再用 \(f(r) - f(l - 1)\) 即可
然后将数字 \(x\) 拆成一个个数位的,也就是个、十、百、千、万……
数位,如个位、十位、百位等,单个数码(比如十进制,此处就是指0∼9)在数x中所占据的一个位置
在代码中的表现为:
- \(a[1 \sim len]\) :将数字拆分为 \(R\) 进制,用数组储存,\(a[i]\) 表示在 \(R^{i - 1}\) 处的系数
- 比如十进制数字 4321 ,转化为a数组后,a[4] = 4, a[3] = 3, a[2] = 2, a[1] = 1
typedef long long ll;
ll solve (ll x) {
int len = 0;
while (x) {
a[++len] = x % 10;
x /= 10;
}
return dfs (...);
}
时间复杂度分析
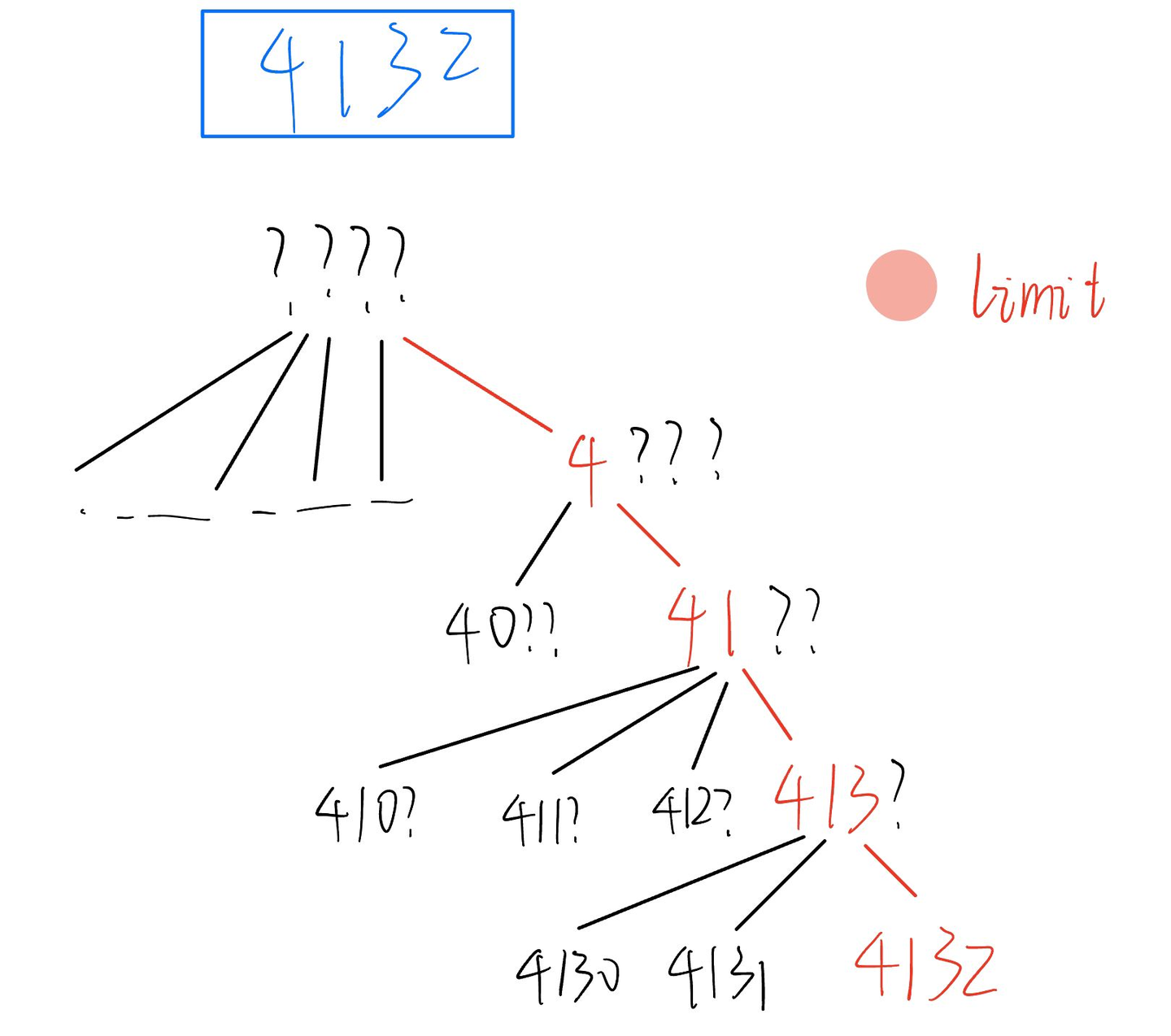
例题
例题0:烦人的数学作业
求解区间 \([L,R]\) 中所有数的数位和之和
数位和:一个数的所有数位上的数字加起来的和,比如313的数位和为3+1+3=7
共 \(1 \le T \le 20\) 组数据,其中\(1 \le L \le R \le 10^{18}\)
在做题之前我们需要将这题需要用到的一些参数声明一下
- \(pos\) :表示当前枚举到的位置,一般从高到低
- \(limit\) :bool 型变量,表示枚举的 pos 位是否收到限制
- 1:表示受限,取到的数不能大于 a[pos]
- 0:不受限,可以取到 [0, R - 1]
- \(sum\) :表示当前 \(len \to (pos + 1)\) 的数位和
如果我们直接进行 dfs 搜索的话,时间复杂度为 \(O(10^{len})\) ,这是我们不能接受的
所以我们记录 \(f[pos][sum]\) 表示:
- 位置 \([pos + 1, len]\) 都已经填写完毕,且这些数位之和为 \(sum\) 的情况下,数位 \([1,pos]\) 任意填写(即 limit 为0)
- \(f[pos][sum]\) 为满足约束的所有数的数位和之和
这样我们就可以写出 dfs 的代码
memset (f, -1, sizeof f);
ll dfs (int pos, int sum, bool limit) {
if (!pos) return sum;
if (!limit && ~f[pos][sum])
return f[pos][sum];
int up = limit ? a[pos] : 9;
ll res = 0;
for (int i = 0; i <= up; i++) {
res += dfs (pos - 1, sum + i, limit && i == up);
}
if (!limit) f[pos][sum] = res;
return res;
}
ll solve (ll x) {
int len = 0;
while (x) {
a[++len] = x % 10;
x /= 10;
}
//这里可以看做一开始顶着 0 的上界
return dfs (len, 1, 0);
}
dfs函数常用的参数
- \(pos\) :表示当前枚举到的位置,一般从高到低
- \(limit\) :bool 型变量,表示枚举的 pos 位是否收到限制
- 1:表示受限,取到的数不能大于 a[pos]
- 0:不受限,可以取到 [0, R - 1]
- \(last\) :表示上一位(第 pos + 1 位)填写的值
- 往往用于约束了相邻数位关系的题目
- \(lead0\) :bool 型,表示是否有 前导零 ,即在 \(len \to (pos + 1)\) 这些位置是不是都是 前导零
- 基于常识,我们往往默认一个数没有前导零,也就是最高位不能为 0
- 只有没有前导零的时候,才能计算 0 的贡献
- 前导零何时跟答案有关?
- 统计 0 的出现次数
- 相邻数字的差值
- 以最高位为起点确定的奇偶位
- \(sum\) :表示当前 \(len \to (pos + 1)\) 的数位和
- \(r\) :表示整个数前缀取模某个数 \(m\) 的余数
- 一般会用在:约束中出现了能被 \(m\) 整除
- 也可以扩展为数位和驱魔的结果
- \(st\) :用于状态压缩
- 对一个集合的数在数位上出现次数的奇偶性有要求时,其二进制形式就可以表示每个数出现的奇偶性
例题1:数字计数
给定两个正整数 \(a\) 和 \(b\) ,求 \([a,b]\) 中的所有整数中,每个数码各出现了多少次。
\(1 \le a \le b \le 10^{12}\)
这道题因为要统计每个数码出现的次数,所以我们要考虑前导零的问题(lead0)
假设当前要统计的数字为 digit ,我们设状态:\(f[pos][cnt]\)
- 当前面已经填过非零的数码时(没有前导零)并且没有上界,在 \([pos + 1, len]\) 中填了 \(cnt\) 个 \(digit\) ,\([1 \sim pos]\) 任意填
- 当 \(limit = 0\) 且 \(lead0 = 0\) 时,显然 \(0 \sim 9\) 的出现次数相同,所以我们只需记 \(f[pos][cnt]\) 即可
- 所以 \(f[pos][cnt]\) 表示满足约束的数中 \(digit\) 出现的次数的总和
由此得到这道题的 dfs
ll dfs (int pos, int cnt, bool limit, bool lead0) {
if (!pos) return cnt;
//引用,方便后面的判断以及赋值
auto &now = f[pos][cnt];
if (!lead0 && !limit && ~now) return now;
int up = limit ? a[pos] : 9;
ll res = 0;
for (int i = 0; i <= up; i++) {
int tmp = cnt + (digit == i);
//这里如果有前导零,并且统计的是 0 ,那么 cnt 归零
if (lead0 && digit == 0 && i == 0) tmp = 0;
res += dfs (pos - 1, tmp, limit && (i == up), lead0 && (i == 0));
}
//如果没有限制,复用
if (!lead0 && !limit) now = res;
return res;
}
例题2:windy数
相邻两个数码之差至少为 2 (不包括前导零)的正整数被称为 windy 数。求在 \([a,b]\) 中有多少个 windy 数? \(1 \le a, b \le 1e9\)
这道题约束了数位相邻间的关系,所以我们要记录一个 \(last\)
设 \(f[pos][last]\) 表示:
- 集合:当前填到第 \(pos\) 位,\([pos + 1, len]\) 位已经填好,上一位(pos + 1)为 \(last\) ,\([1,pos]\) 随便填
- 值:满足约束的数字个数
因为 相邻两个数码之差至少为 2(不包括前导零) ,所以我们需要对有没有前导零进行分类讨论,并且要记录是否有前导零,因为有没有前导零的状态是不同的
得出 \(dfs\)
int dfs (int pos, int last, int lead0, int limit) {
if (!pos) return 1;
auto &now = f[pos][last];
if (!lead0 && !limit && ~now) return now;
int up = limit ? a[pos] : 9;
int res = 0;
for (int i = 0; i <= up; i++) {
//如果没有前导零,并且当前要填的数码与上个数码之差 < 2,不合法,跳过
if (!lead0 && abs (i - last) < 2) continue;
res += dfs (pos - 1, i, lead0 && (i == 0), limit && (i == up));
}
if (!lead0 && !limit) now = res;
return res;
}
例题3:花神的数论题
设 \(sum(i)\) 表示 \(i\) 的二进制表示中 1 的个数。给定一个 \(N\) ,求出 \(\prod_{i=1}^{N}sum(i)\) ,答案 mod 1e7+7
这道题同样是求一个数中某个数码的出现次数,所以我们可以设 \(f[pos][cnt]\) 表示:
- 集合:填完 \([pos + 1, len]\) 位,出现 \(cnt\) 个 1 ,\([1, pos]\) 位随便填
- 值:满足约束的所有数,每个数 1 的个数的乘积
注意,这道题的幺元为 1 ,因为要求乘积。还有如果枚举到 0 ,要返回 1
ll dfs (int pos, int cnt, int limit) {
if (!pos)
return max (cnt, 1);
auto &now = f[pos][cnt];
if (!limit && ~now) return now;
int up = limit ? a[pos] : 1;
ll res = 1;
for (int i = 0; i <= up; i++) {
cnt += (i == 1);
res *= dfs (pos - 1, cnt, limit && (i == up));
res %= mod;
}
if (!limit) now = res;
return res;
}
例题4:Round Numbers S
如果一个正整数的二进制表示中,0 的数目不小于 1 的数目,那么它就被称为「圆数」。
例如,9 的二进制表示为 1001,其中有 2 个 0 与 2 个 1。因此,9 是一个「圆数」。
请你计算,区间 [l,r] 中有多少个「圆数」。
对于 100% 的数据,\(1 \le l, r \le 10^9\)。
这道题中答案的统计与 0、1 的个数相关,所以我们要统计 \(cnt0, cnt1, lead0\)
设 \(f[pos][cnt0][cnt1]\) 表示:
- 集合:填完 \([pos + 1, len]\) 位,出现 \(cnt0\) 个 0 ,\(cnt1\) 个 1, \([1, pos]\) 位随便填
- 值:集合中所有满足条件的数的个数
int dfs (int pos, int cnt0, int cnt1, bool lead0, bool limit) {
if (!pos)
return cnt0 >= cnt1;
int &now = f[pos][cnt0][cnt1];
if (!lead0 && !limit && ~now) return now;
int up = limit ? a[pos] : 1;
int res = 0;
for (int i = 0; i <= up; i++) {
bool pre0 = lead0 && (i == 0);
int s0 = pre0 ? 0 : cnt0 + (i == 0);
int s1 = pre0 ? 0 : cnt1 + (i == 1);
res += dfs (pos - 1, s0, s1, pre0, limit && (i == up));
}
if (!lead0 && !limit) now = res;
return res;
}
例题5:Magic Numbers
给定 4 个整数 \(m,d,l,r\) ,保证 \(l,r\) 位数相同。
问满足以下条件的数 \(x\) 的个数:
1)\(l≤x≤r\)
2)\(x\) 的偶数位是 \(d\),奇数位不是 \(d\)。 (这里定义偶数位为从高位往低位的数的偶数位)
3)\(m|x\)
答案对 \(1000000007\) 取模。
\(1≤m≤2000,0≤d≤9,1≤l≤r≤10^{2000}\)
好恶心
这道题中我们需要统计的参数:
- \(r\) :最终的数 \(x\) ,因为 \(m \mid x\)
- \(even\) :是否为偶数位
这里我们要考虑一个问题,我们是否需要记录前导零?
- 因为跟最高位有关,但最高位不一定是 \(len\) ,所以要加?
但是题目中给了一个约束,保证 \(l, r\) 位数相同
我们默认我们搜索出来的所有数,都是允许含有前导零的len位数,因为l,r是不含有前导零的len位数字,所以那些不含有前导零的小于len位的数字,就会在二者答案相减的时候被扣除掉(也就是说不含前导零小于len位数的那些数,我们计数错了也没有关系)
设 \(f[pos][r]\) 表示:
- 集合:已经填完 \([pos + 1, len]\) 位,已经填好的数码组成的数 \(x \bmod m = r\) ,\([1, pos]\) 随便填
- 值:所有满足条件的数的个数
ll dfs (int pos, int r, bool even, bool limit) {
if (!pos) return (r == 0);
ll &now = f[pos][r];
if (!limit && ~now) return now;
int up = limit ? a[pos] : 9;
ll res = 0;
int ne = even ^ 1;
if (even) {
if (d <= up) {
res += dfs (pos - 1, (r * 10 + d) % m, ne, limit && (d == up));
res %= mod;
}
} else {
for (int i = 0; i <= up; i++) {
if (i == d) continue;
res += dfs (pos - 1, (r * 10 + i) % m, ne, limit && (i == up));
res %= mod;
}
}
if (!limit) now = res;
return res;
}
如果 \(l, r\) 不保证位数相同呢?
我们就需要加上 \(lead0\) ,并且状态变成 \(f[pos][r][0/1]\) 表示:
- 集合:\([pos + 1, len]\) 已经填完,并且填好的数码组成的数字 \(x \bmod m = r\) ,\(pos\) 位为从最高位开始的 偶/奇 数位,\([1, pos]\) 随便填
- 值:所有满足约束的数的个数
例题6:手机号码
手机号码 11 位,求出 \([l, r]\) 中满足以下条件的号码
- 号码中必须出现某三个相邻的数字相同
- 号码中不能同时出现 4 和 8
号码一定是 11 位 ,\(10^{10} \le l \le r < 10^{11}\)
这道题要用的参数
- \(last1\) :\(pos + 1\) 位填的数,如果没有为 10
- \(last2\) :\(pos + 2\) 位填的数,如果没有为 10
- \(have4\) :是否出现过 4
- \(have8\) :是否出现过 8
- \(lead0\) :前导零
设 \(f[pos][la1][la2][ok][have4][have8]\) 表示:
- 集合:\([pos + 1, len]\) 已经填好,上位为 \(la1\) ,上上位为 \(la2\) ,是/否 满足第一个条件,是/否 出现过 4,是/否 出现过 8,\([1, pos]\) 随便填
- 值:集合中满足约束的数的个数
ll dfs (int pos, int la1, int la2, bool ok, bool h4, bool h8, bool limit, bool lead0) {
if (!pos) return ok && !(h4 && h8) ? 1 : 0;
if (h4 && h8) return 0;
auto &now = f[pos][la1][la2][ok][h4][h8];
if (!limit && !lead0 && ~now) return now;
ll res = 0;
int up = limit ? a[pos] : 9;
for (int i = 0; i <= up; i++) {
int nok = ok || (i == la1 && i == la2);
if (lead0) nok = 0;
res += dfs (pos - 1, i, la1, nok, h4 || (i == 4), h8 || (i == 8), limit && (i == up), lead0 && (i == 0));
}
if (!limit && !lead0) now = res;
return res;
}
ll solve (ll x) {
// if (x < 1e10) return 0;
len = 0;
while (x) {
a[++len] = x % 10;
x /= 10;
}
return dfs (len, 10, 10, 0, 0, 0, 1, 1);
}
例题7:CF885E Slytherin's Locket
求 \(l...r\) 之间转成 \(b\) 进制后,\(0,1,2...,b - 2, b - 1\) 都出现偶数次的数的个数。
\(1 \le q \le 10^5 \ ,\ 2 \le b \le 10 \ , \ 1 \le l \le r \le 10^{18}\)
因为要记录一个集合中各个元素的出现次数,且只与奇偶性相关,那么我们可以用一个 \(st\) 来表示集合的状态
参数:
- \(st\) :表示 \(0 \sim b - 1\) 中每个数出现的奇偶性
- \(lead0\) :是否含有前导零,因为要统计 0 的出现次数
\(f\) 数组中设出进制 \(b\) 可以复用,毕竟 \(b \le 10\)
设 \(f[b][pos][st]\) 表示:
- 集合:\(r\) 进制,\([pos + 1, len]\) 已经填好,\(0 \sim r - 1\) 各个数出现次数的奇偶性,\([1,pos]\) 随便填
- 值:集合中满足约束的数的个数
ll dfs (int b, int pos, int st, bool lead0, bool limit) {
if (!pos) {
for (int i = 0; i < b; i++) {
if (st & (1 << i)) return 0;
}
return 1;
}
auto &now = f[b][pos][st];
if (!limit && !lead0 && ~now) return now;
ll res = 0;
int up = limit ? a[pos] : b - 1;
for (int i = 0; i <= up; i++) {
bool pre0 = lead0 && (i == 0);
if (pre0) res += dfs (b, pos - 1, st, pre0, limit && (i == up));
else res += dfs (b, pos - 1, st ^ (1 << i), pre0, limit && (i == up));
}
if (!limit && !lead0) now = res;
return res;
}
例题8:Balanced Numbers
一个数被称为是平衡的数,当且仅当对于所有 出现过 的数码(即 0−9 ),每个偶数出现奇数次,每个奇数出现偶数次。给定 A,B,请统计出 [A,B] 内所有平衡数的个数。
\(1≤A≤B≤10^{19}\)
这道题跟前一道题很相似,也是对数码的出现次数的奇偶性做出了限制
注意,这题的坑在于 当且仅当对于所有 出现过 的数码 ,重点在于出现过,也就是没有出现过的数码我们是不用管的
设 \(f[pos][st][v]\) 表示:
- 集合:\([pos + 1, len]\) 已经填完,已经填完的数的数码的奇偶性集合为 \(st\) ,数码的出现情况为 \(v\) , \([1, pos]\) 位任意填
- 值:集合中满足条件的数的个数
dfs
ll dfs (int pos, int st, int v, bool lead0, bool limit) {
if (!pos) {
for (int i = 0; i <= 9; i++) {
if (!(v & (1 << i))) continue;
if ((i & 1) && (st & (1 << i))) return 0;
if (!(i & 1) && !(st & (1 << i))) return 0;
}
return 1;
}
auto &now = f[pos][st][v];
if (!limit && !lead0 && ~now) return now;
ll res = 0;
int up = limit ? a[pos] : 9;
for (int i = 0; i <= up; i++) {
int pre0 = lead0 && (i == 0);
if (pre0) {
res += dfs (pos - 1, v, st, pre0, limit && (i == up));
} else {
res += dfs (pos - 1, st ^ (1 << i), v | (1 << i), pre0, limit && (i == up));
}
}
if (!limit && !lead0) now = res;
return res;
}
例题9:XOR Sum
给定三个整数 \(n,m,k \ (0 ≤ n ≤ 10^{15},0≤m≤10^{12},1≤k≤18)\) ,求解有多少个长度为 \(k\) 的数组 \(a[1⋯k]\) 满足如下约束:
(1) \(0≤a[i]≤m\)
(2)\(\displaystyle \left(\sum_{i = 1}^k\sum_{j = 1}^{i - 1}a[i] \oplus a[j] \right)=n\)
其中 \(\oplus\) 表示异或运算,答案 \(\bmod 1e9 + 7\)
我靠,真他妈恶心
这道题和常见的数位dp的形式不太一样,以往的数位dp我们都是一位一位填数,但这里显然不能这么做,而且要统计他们异或起来的贡献,并不好做。所以这里我们要 \(k\) 个数一起一位一位地填
因为这题的限制条件有二进制的异或,所以我们把每个数拆分成二进制来考虑,那么每一位要么填 0 要么填 1 ,观察式子,发现其实就是从这些数里任意选两个数的组合 \(C_k^2\) ,将选中的两个数异或,\(\sum a[i] \oplus a[j]\) 就是答案
那我们对每一位进行讨论的时候,就可以考虑这一位有多少数填 1 多少数填 0 ,但是可能有些数的这一位是收到限制的,所以我们定义 \(s\) 表示 \(pos\) 位有多少数收到限制,也就是有 \(s\) 个数的这一位不能超过 \(b[pos]\) (\(b[]\) 是将 \(m\) 二进制拆分后得到的每一位)
需要用到的参数:
- \(s\) :到第 \(pos\) 位有多少数收到限制
- \(sum\) :前面填过的数的贡献为多少,最后要求 \(sum = n\)
分情况讨论受限情况
-
\(b[pos] = 1\) ,设在有限制的 \(s\) 个数中选了 \(i\) 个 1 ,在没有限制的 \(k - s\) 个数中选了 \(j\) 个 1 :
-
产生的贡献 :\(v = 2^{pos} * (i + j) * (k - i - j)\)
-
方案数为:\(\displaystyle tmp = \binom{s}{i} * \binom{k - s}{j}\)
-
下一个状态 \(s = i\)
-
-
\(b[pos] = 0\) ,设在没有限制的 \(k - s\) 个数中选了 \(j\) 个 1
- 产生的贡献:\(v = 2^{pos} * j * (k - j)\)
- 方案数为:\(\displaystyle tmp = \binom{k - s}{j}\)
- 下个状态 \(s = s\)
设 \(f[pos][s][sum]\) 表示:
- 集合:\([pos + 1, len]\) 已经填完,第 \(pos\) 位有 \(s\) 个数受限,已经填完的数的贡献为 \(sum\) ,\([1, pos]\) 随便填
- 值:集合中满足约束的数的个数
这里 \(sum\) 是个 \(1e15\) 级别的数,但是合法状态数比较少,所以我们可以用 \(map\) 来存,map<ll, ll> f[N][N]
但是这样的时间复杂度还是有些高,考虑剪枝:
- \(sum > n\) 退出
- 考虑剩下的每一位都按照 一半填 1 一半填 0 的策略填数,的到最大贡献 \(X = 2^{pos + 1} - 1 * (k / 2) * (k - k / 2)\) ,如果 \(sum + X < n\) ,退出



 浙公网安备 33010602011771号
浙公网安备 33010602011771号