索引-建立框架篇
在本篇文章中,开始部分会介绍索引的定义,及常见索引使用的数据结构和 MySQL 的索引模型。然后,根据索引的存储结构来学习索引的建立原则。最后会介绍索引的使用场景。在阅读后,应该了解如下的内容:
- 索引场景的模型:哈希表,有序数组和搜索树
- MySQL 的索引模型,了解主键/非主键索引,回表,页分裂的概念
- MySQL 建立索引的原则
索引概述
索引的定义
索引常被用来根据明确的列值来快速找到对应的行。如在 MySQL 中,没有索引的话,在找到数据时,会从表的第一行开始,遍历整个表。对于大表来说,代价常常很大。而对于有索引的表来说,可以在不遍历整个表的情况下,很快决定出数据文件的中间位置,再进行查找。
索引常用的数据结构
索引常常会用到哈希表,有序数组和搜索树作为常见的存储结构。
一、哈希表
定义:
哈希表就是常见的 Key/value 的存储结构。在实现上,通过哈希函数通过 key 算出一个确定的位置,将值保存在对应位置的数组中。
下图中,数组保存了 1 到 Z 个位置。其中 key 为用户的身份证号。value 为对应用户的身份信息。
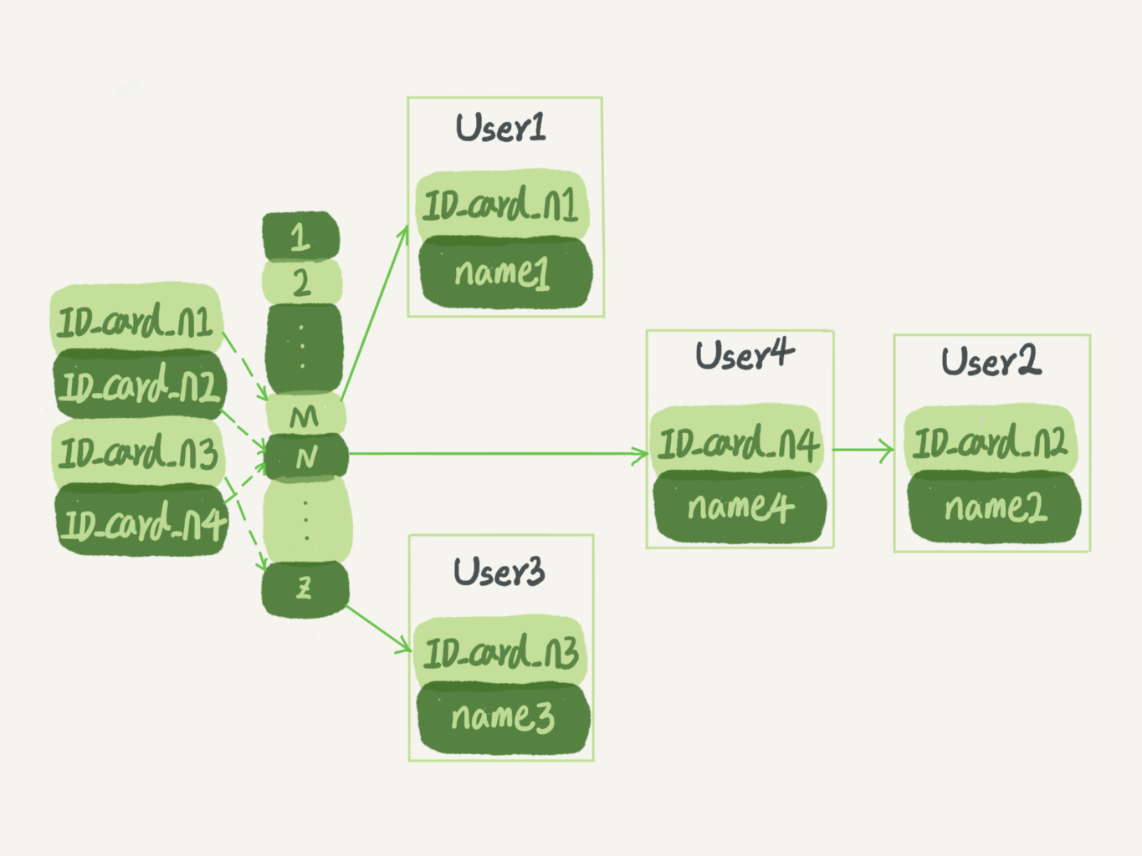
存在的问题:
如上图中,在位置为 N 的数组上,身份证号为 N2 和 N4 的用户,在通过哈希函数计算后,得到了相同的位置 N. 这就是所说的哈希冲突。为了解决这个问题,一种常见的方法是,在冲突的位置拉出一个链表。
假如想要找到身份证号 n2 的用户名称。就先需要通过哈希函数计算出保存的位置 N,然后在 N 的位置上进行遍历,找到 User2.
适用的场景:
由于数组中的 ID_card_n 的保存位置不是递增的,在增加用户时很快,直接向后追加。但由于不是有序的,在区间查询时,速度很慢。比如要查找 [ID_card_x, ID_card_y] 区间用户,需要全部扫描一遍。
所以,哈希表这种结构适用于只有等值查询的场景,比如 Memcached 及其他一些 NoSQL 引擎。
二、有序数组:
定义:
简单来说,数组数据的会按照一定的顺序进行保存。
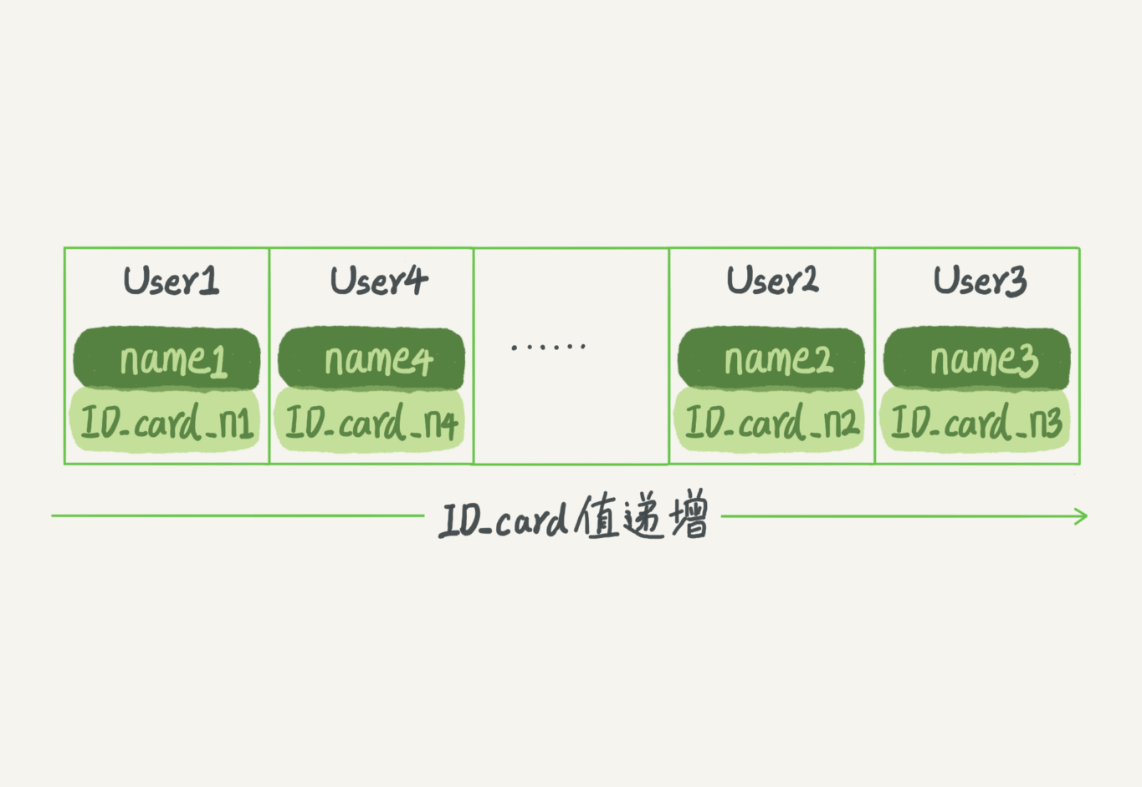
存在的问题:
在更新时,如在中间插入一个记录需要挪动后面所有的记录,成本很高。
适用的场景:
在等值查询或者范围查询的场景中性能非常优秀。
比如在图中,是按照身份证的大小保存的数据。这时在查找某一用户的名称事,可以使用二分法来查找,时间复杂度为O(log(N))。
在范围查询时,要查 [ID_card_X, ID_card_Y] 区间的用户,可以使用二分法找到 X 的位置,然后向右遍历到 Y 就可以了。
所以有序数组索引只适用于静态存储引擎,如 2017 年某个城市的所有人口信息,这类不会再修改的数据。
三、搜索树
为了平衡和更改时,整体的效率,搜索树作为进一步的选择。
拿二叉搜索树举例
在二叉搜索树中,每个节点的左儿子小于父节点,父节点小于右儿子。
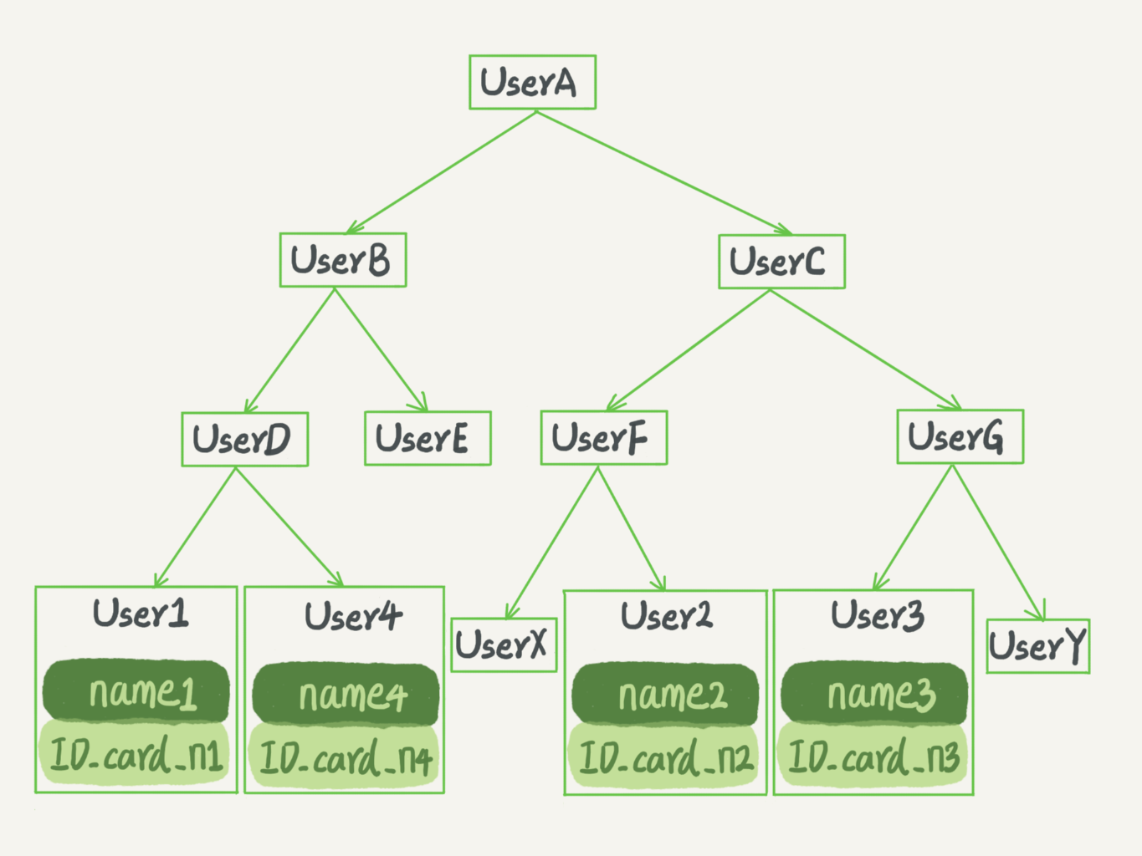
假如要查找 ID 为 ID_card_n2 的节点,在查找时会按照 UserA -> UserC -> UserF -> User2 的顺序,时间复杂度为 O(log(N)).
为了维持 O(log(N)) 的查询复杂度,同时也要保证该树是平衡二叉树。在更新时,复杂度也是 O(log(N)).
在实际场景中,一般选用 N 叉树,而不是二叉。
树可以有二叉,也可以有多叉。多叉树就是每个节点有多个儿子,儿子之间的大小保证从左到右递增。二叉树是搜索效率最高的,但是实际上大多数的数据库存储却并不使用二叉树。其原因是,索引不止存在内存中,还要写到磁盘上。
如果采用二叉树的结构,查询效率会很低。因为在机械硬盘时代,从磁盘随机读一个数据块的时间大致为 10ms 左右的寻址时间。对于 100 万行的表,也就是 100 万个节点的平衡二叉树,树高 20. 也就需要访问 20 个数据页(每个叶子节点就是一个页,每个页包含两个数据,页之间通过链式方式链接。)单独访问一行可能需要 20 * 10ms=200ms 毫秒的时间,查询的速度太慢。
为了减少查询磁盘的数量,就必须在查询过程中尽量少访问数据块。所以 N 叉树就派上了用场。N 取决于数据块的大小。
以 InnoDB 的整数字段索引为例,N 差不多是 1200. 也就是说,树高为 4 的时候,可以存储 1200^3 约 3 亿的值。
考虑到树根的数据块总是在内存中的,一个 10 亿行的表上一个整数字段的索引,查找一个值最多只需要访问 3 次磁盘。其实,树的第二层也有很大概率在内存中,那么访问磁盘的平均次数就更少了。
数据库发展到今天,很多的新的数据机构如跳表,LSM 树等都被用于在引擎设计中。但数据库的底层核心就是之前的这些数据模型,后面的新模型只不过是不断迭代,不断优化的结果。在每次遇到一个数据库时,先首先关注它的数据模型,进而才能分析出其使用的场景。
MySQL 中的索引模型
索引组织表
在 InnoDB 中,表都是根据主键顺序以索引的形式存在,这种存储方式称为索引组织表。
InnoDB 中使用了 B+ 树作为索引模型,每一个索引在 InnoDB 中都对应一颗 B+ 树。
主键索引和非主键索引
根据叶子节点的内容,分为主键索引和非主键索引。
主键索引中存的是整行数据。在 InnoDB 里,主键索引也被称为聚簇索引。
非主键索引的叶子节点内容是主键的值。在 InnoDB 里,非主键索引也被称为二级索引。
如有一个主键为 ID,有字段 K 的表,其中 K 上有索引。
mysql> create table T(
id int primary key,
k int not null,
name varchar(16),
index (k))engine=InnoDB;
那么对应的 B+ 树的结构就如下面所示:
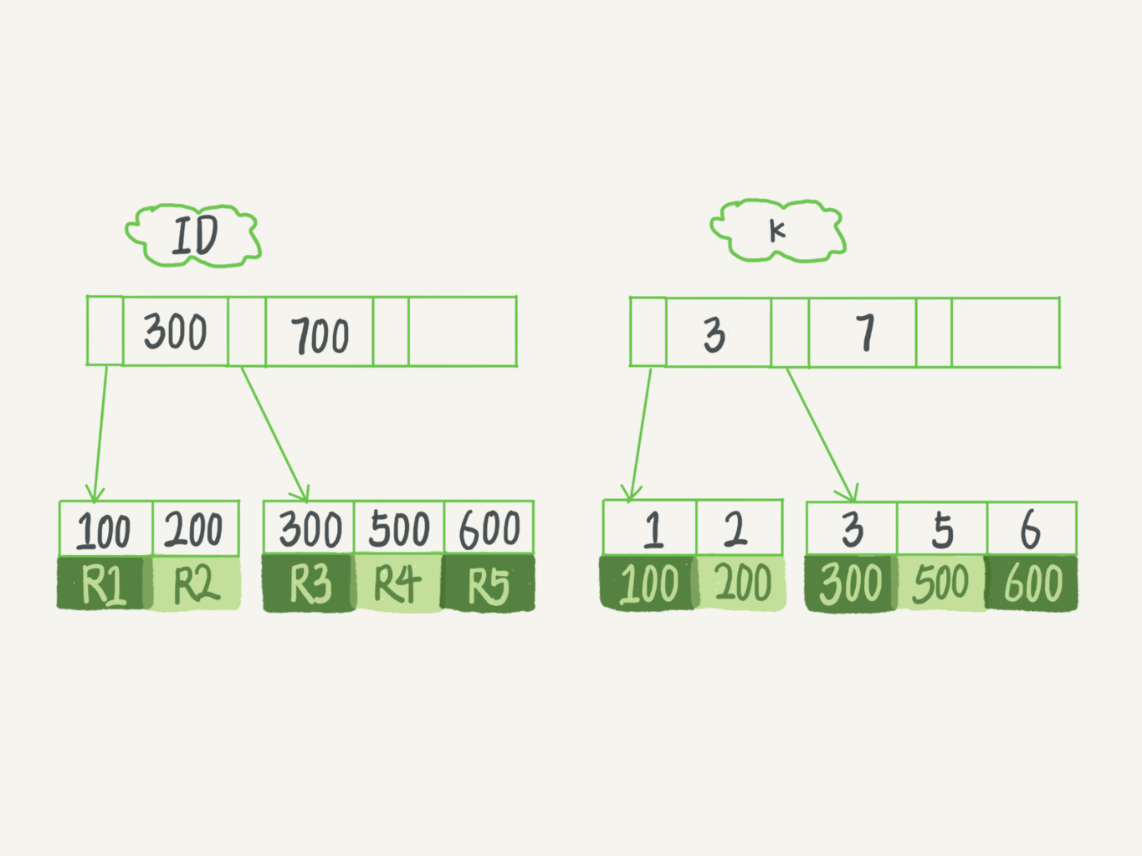
图中有 ID 的表示主键索引,而 K 的就是非主键索引。如在查询时执行 select * from T; 这时仅需要搜索 ID 这棵 B+ 树。
如果语句是select * from T where k=500;, 就先需要搜索 k 这棵 B+ 树,然后再搜索 ID 这棵 B+ 树。其实这个过程就是称为回表的过程。因为 K 这棵树仅仅存储了 ID 的信息,而没有正行的数据,想要搜索全部的数据,需要通过 ID 这棵 B+ 树来查询。
所以基于回表的情况,非主键索引的查询需要多扫描一棵索引树。因此,在应用中应该尽量使用主键查询。
InnoDB 中索引的维护
B+ 树为了维护索引有序性,在插入新值的时候需要做必要的维护。以上图为例,如果插入新的行 ID 值为 700,则只需要在 R5 的记录后面插入一个新记录。如果新插入的 ID 值为 400,就相对麻烦了,需要逻辑上挪动后面的数据,空出位置。
更糟时,如果 R5 所在数据页已经存满,根据 B+ 树的算法,这时候需要申请一个新的数据页,然后挪动部分数据过去。这个过程称为页分裂。在这种情况下,性能自然会受影响。
除了性能外,页分裂操作还影响数据页的利用率。原本放在一个页的数据,现在分到两个页中,整体空间利用率降低大约 50%。
为了防止这种情况,当相邻两个页由于删除了数据,利用率很低之后,会将数据页做合并。合并的过程,可以认为是分裂过程的逆过程。
自增主键的原理
在一些建表规范里,要求建表语句里一定要有自增主键。来分析下是否正确。
在性能方面,如果设置了自增主键 NOT NULL PRIMARY KEY AUTO_INCREMENT. 在插入新记录时,就可以不指定 ID 的值,系统会获取当前 ID 的最大值加 1 作为下一条记录的 ID。也就是说,这样就符合了递增插入的场景,每次插入,都是追加操作。不会挪动其他记录,也不会触发叶子节点的分裂,自然性能也就不会出现问题。
而使用业务逻辑做主键时,不能保证有序的插入,这样在写数据时,会出现页分裂的情况,成本较高。
在存储空间方面,主键长度越小,普通索引的叶子节点就越小,普通索引占用的空间也就越小。比如如果使用身份证号的字符串作为主键,每个非主键索引的叶子节点都是字符串类型的值,那么每个二级索引(非主键索引)的叶子节点占用约 20 个字节,如果使用整型做主键,仅仅需要 4 个字节,长整型(bigint)则是 8 个字节。
所有考虑到性能和存储,自增是更合理的选择。但什么场景可以使用业务字段呢,就是该表只有一个索引,且是唯一索引。也就是典型的 K/V。
由于没有其他索引,所以不用考虑二级索引的存储大小。考虑到上一段提到的“尽量使用主键查询”原则,直接将这个索引设置为主键,可以避免每次查询需要搜索两棵树。
案例:重建索引的选择
索引可能因为删除,或者页分裂等原因,导致数据页有空洞,重建索引会创建一个新的索引,把数据按顺序插入,这样页面的利用率最高,也就是索引更紧凑、更省空间。
对于表 T 重建二级索引
alter table T drop index k;
alter table T add index(k);
对于表 T 重建主键索引
alter table T engine=InnoDB;
# 注意有人会采用如下的方法
alter table T drop primary key;
alter table T add primary key(id)
# 不论是删除主键还是创建主键,都会将整个表重建。
所以连着执行这两个语句的话,第一个语句就白做了。
MySQL 中的索引原则
覆盖索引
什么是覆盖索引?
覆盖索引时 select 的数据列,可直接通过索引就能取得,而不必通过主键索引获取数据行。
比如,建立这样一个表结构:
mysql> create table T (
ID int primary key,
k int NOT NULL DEFAULT 0,
s varchar(16) NOT NULL DEFAULT '',
index k(k))
engine=InnoDB;
insert into T values(100,1, 'aa'),(200,2,'bb'),(300,3,'cc'),(500,5,'ee'),(600,6,'ff'),(700,7,'gg');
对应索引树的结构如下:

当执行 select * from T where k between 3 and 5;时:
- 会在 k 二级索引树上,找到 k=3 的记录,获取 ID=300.
- 然后在 ID 索引树上,查找 300 对应的行 R3.
- 在 K 索引树上,取得 ID=500.
- 然后在 ID 索引树上,查找 500 对应的行 R4.
- 在 K 索引树上,取 k=6,发现无法取到,退出。
在这个过程中,从 K 索引到主键索引搜索的过程为回表。而此过程一共回表了两次(步骤2,4)。
但当我们执行 select ID from T where between 3 and 5; 时,由于想要查询的 ID 列,已经在 K 二级索引上了,索引就省去了再去搜索主键索引的步骤。换句话说,在这个查询中,k 已经覆盖了我们的查询需求,索引被称为覆盖索引。
需要注意的是,在引擎的内部在索引 K 上其实读了 3 个记录,但对于 Server 层来说,引擎就拿到两条记录,所以会认为扫描行数是 2。
为什么要有覆盖索引?
避免回表,覆盖索引可以减少树的搜索次数,显著提升查询性能,是常见的性能优化手段。
当然,索引字段的维护是有代价的,在建立冗余索引来支持覆盖索引时就需要权衡考虑了。
最左前缀原则
为什么要有最左前缀原则?
有时会面临这样的情况,有一个查询请求不是太频繁,为其单独建立索引不太合适,但走全表扫描不太合适。这时应该怎么办,就可以利用 B+ 树这种索引结构的最左前缀原则来定位。
什么是最左前缀原则?
假如有这样一张市民表:
CREATE TABLE `tuser` (
`id` int(11) NOT NULL,
`id_card` varchar(32) DEFAULT NULL,
`name` varchar(32) DEFAULT NULL,
`age` int(11) DEFAULT NULL,
`ismale` tinyint(1) DEFAULT NULL,
PRIMARY KEY (`id`),
KEY `id_card` (`id_card`),
KEY `name_age` (`name`,`age`)
) ENGINE=InnoDB
对应 name_age 的索引结构如下:
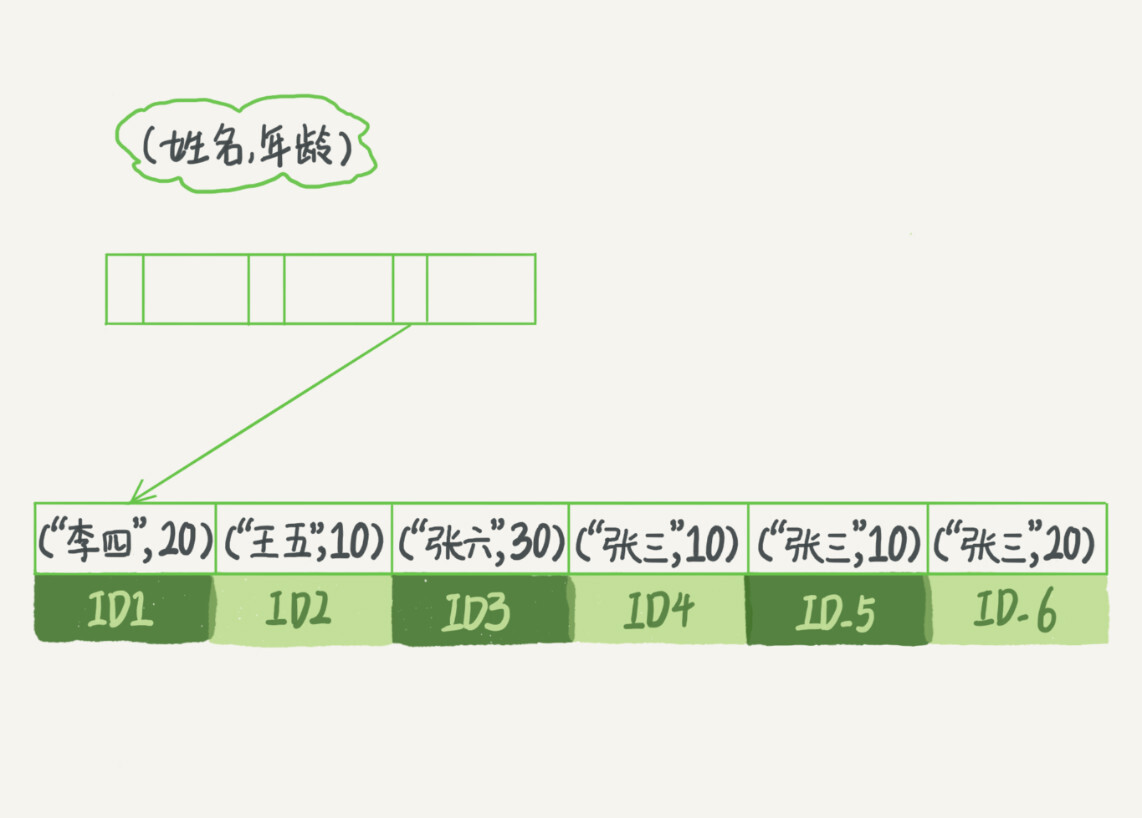
可以看到索引项会按照索引定义里面出现的字段顺序来排序。
当要查找名字是张三的人时,可以快速定位到 ID4, 然后向后找到所有叫张三的人。
同样如果想要查找的是姓张的人where name like '张%',同样也能用上这个索引,会先找到姓张的 ID3 然后向后遍历。
这时可以看到,不仅是满足索引的全部定义的可以使用索引来加速,只要满足最左原则,就可以用该索引进行加速。这个最左前缀可以是联合索引的 N 个字段,也可以是字符串索引的最左 M 个字符。
所以对于联合索引来说,如何安排索引内字段的顺序就变得很重要。这里需要考虑到两方面的内容,首先是索引的复用能力,然后是考虑空间的问题。
对于复用能力,由于支持最左前缀的原则,所以当有(a,b)的联合索引后,一般就不需要再 a 上建立索引了。假如有了两个新的查询,根据身份证号查询名字,根据身份证号查询地址的需求。就可以将身份证号放在联合索引的第一个位置。然后根据名字或地址的请求频率来放置第二个。
对于空间来说,有时会出现既有(a,b)的联合查询,又有基于 a,b 的各自查询。对于查询条件里只有 b 的语句,是无法使用(a,b)的索引的,所以需要再维护一个索引,即 (a,b)和 (b)。还是市民表的情况 ,name 字段比 age 字段大,所以建议创建的是 (name, age) 和 age 索引,而不是(age,name)和 name 索引。
索引下推原则
当满足最左前缀索引时,可以通过它在索引中定位。这时,对于那些不符合最左前缀索引的部分会怎么样呢?
还是拿联合索引(name,age)来举例,如果现在想要查询第一个名字是张,但是年龄是 10 岁的所有男孩,
mysql> select * from tuser where name like '张%' and age=10 and ismale=1;; 在开始部分,可以用张来找到第一个满足条件的记录 ID3。然后在判断其他条件是否满足。
MySQL 5.6 前,做法是通过找到 ID3 后,然后开始回表,一条条的查询记录是否满足条件。注意,这里只会快速定位到 name ,对于 age 无法定位。而是通过回表时,查看 name 的值是否满足。
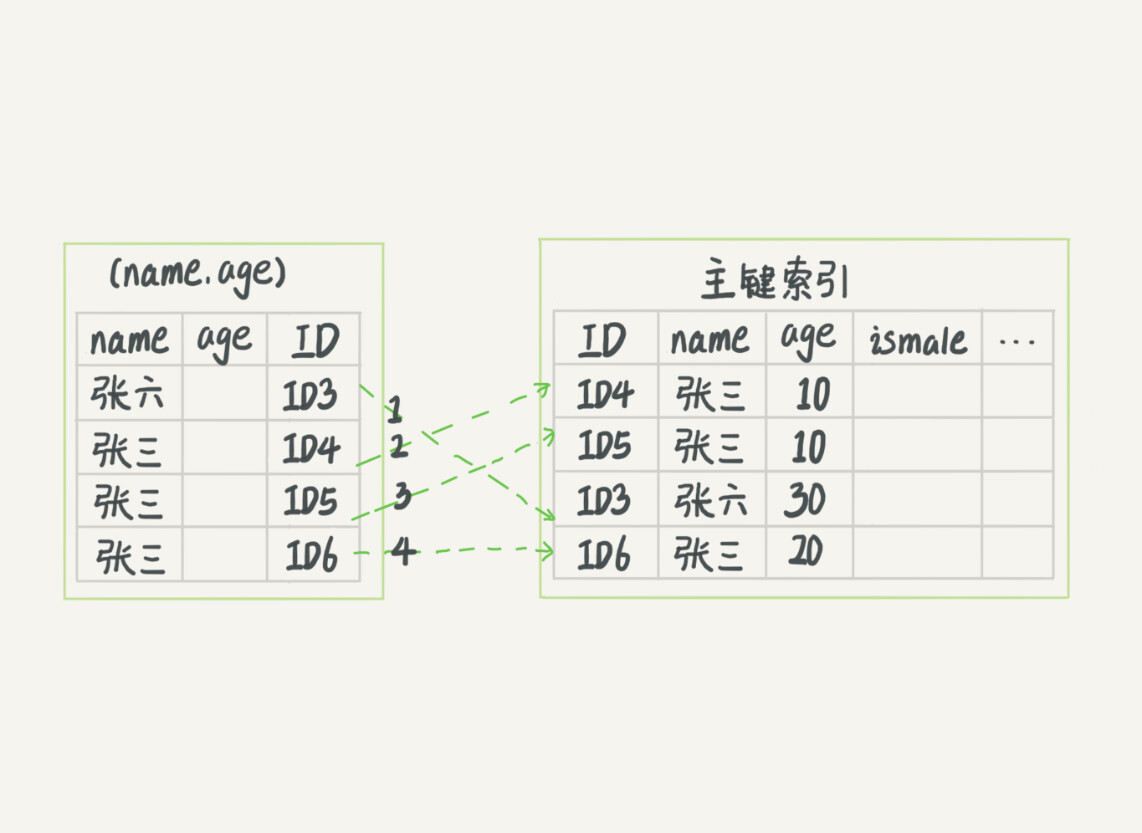
在 5.7 后,引入索引下推优化,在遍历二级索引是,会先对索引包含的列的条件做判断是否满足,然后再直接做过滤,减少回表的次数。简单来说,在(name,age)索引树上就会对 age 进行判断,只有满足条件的才去回表。
总结
总结一下,首先介绍了常见的索引模型有哈希表,有序数组和搜索树。其中哈希表适用于等值查询的场景,在插入时很快,但由于 key 并不是有序的,所以在范围查询表现的很差,并且还存在 hash 冲突的情况。
有序数组由于有序的特点,在等值查询和范围查询都很快,但不适合修改数据。所以有序数组适用于那些数据不会轻易改变的场景。
搜索树是为了平衡和查询的关系,在实际中一般使用 N 叉树,其中 N 取决于数据块的大小。
之后介绍了,MySQL InnoDB 引擎中,采用的是 B+ 的数据模型,并解释了由于 B+ 树的特点,如果不使用自增主键时,会出现页分裂的情况,从而造成性能的降低。
如果出现数据页存在空洞现象比较多的情况,可以采用重建索引的方式。
最后介绍了建立索引的了三个原则:
- 覆盖索引:在建立索引时包含常见的搜索列,从而减少回表的次数。
- 最左前缀原则:在建立联合索引时,要在空间和复用性考虑,利用 B+ 树,会匹配联合索引第一个字段或者第一个字段的前 N 个字符做匹配。
- 索引下推:介绍了当查询的内容大于索引的内容,无法利用覆盖索引时。会根据最左前缀原则,根据查找的条件先过滤,然后再回表,从而减少回表的次数。达到性能的提升。
参考
题外话:最近在系统的学习 MySQL,推荐一个比较好的学习材料就是<<丁奇老师的 MySQL 45 讲>>,链接已经附在文章末尾。
文章中很多知识点就是从中学来,加入自己的理解并整理的。
大家在购买后,强烈推荐读一读评论区的内容,价值非常高,不少同学问出了自己在思考时的一些困惑。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号