三年级小学生日记范文

也可以叫做补题日记（二）。

这个时候有人就要问了，“主播主播，你的《补题日记》《补题周记》《杂题不讲》《一些问题》《随便什么标题。》难道不更了吗？”

对此，我的回答是：

（当然，我現在只是在打比方）
正如沉睡的大腦從随機事件的記憶中拼接出虚幻之叙事一般
清醒的心智也必须從互連網的虚構查層中编織出愛
没有關於愛的表情包。
愛麗絲從夢中醒来只有爱是永無止鏡的。
事实：愛永無止息地預演著自身之消亡
亦施行著自身之解体。
（当然，我现在只是在打比方）
愛掏空了康復的所有可能性，一張通往健康終点的单程票。
爱的唯一熱情在於吞噬一切再次墜入爱河的可能性。
「愛-恢復」循環，亞里士多德的自我滋養：
対災異之奢欲，於其飄忽的党展中处如可見。驱力：对残酷的渴慕，
這豢養了每一種可憎的自我貶損、窘迫和愚蠢。
赢得了理所応當的軽蔑，每一個姿態就成了徹底燃滅的折损
沉溺在這種折磨中，唯有下跪、慟哭
泣血、哀求，「請饒恕我……」
哭声，呼喊声，纷扰的人影。
但愛是永無止境的，我愛你。

A - JamBrains（已过）

设 \(f(x,y)\) 表示从 \((x,y)\) 开始按下 \(u\) 次上键再按下 \(r\) 次右键后能到达的位置。容易发现若 \((x_a,y_a)\leq (x_b,y_b)\)，则 \(f(x_a,y_a)\leq f(x_b,y_b)\)。此处二元组的偏序关系就是一个普通的定义。

根据这个可以得到一个推论，若 \(f(x,y)\geq (x,y)\)，则 \(f(f(x,y))\geq f(x,y)\geq (x,y)\)，也就是说 \(f^k(x,y)\geq (x,y)\)。即，若 \((x,y)\) 不在第一行且 \(f(x,y)\geq (x,y)\)，那么 \((x,y)\) 永远不可能到达第一行。

还有一个推论是合法的位置是一段前缀，这是显然的。就是把这些位置铺平后的一段前缀。

根据如上推论，可以得到一个重要性质：一行的位置要么同时合法，要么同时不合法。

怎么证明？图灵证明症。

11；；1；1；1；1；；1；1；1；11；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；1；11；1；1；1；1；；111；1；1；1；1；1；1；11；1；1；1；11；1；；1；11；1；1；1；1；1；1；1；1；1；1；11；1；1；；1；1；1；1；1；1；1；1；1；1；11；1；1；1；1；；1；1；1；1；1；1；；1；1；11；11；；1；1；1；1；1；1；1；1；；；1；1；1；1；1；1；；

其实这是摩斯电码。

考虑归纳，最开始前 \(u+1\) 行一定都是合法的。假设现在算到了第 \(i\) 行，前 \(i-1\) 均合法。现在，第 \(i\) 行 \(1\sim x\) 这些位置合法，\(x+1\sim s_i\) 这些位置不合法。那么，\(f(i,x+1) \geq (i,x+1)\) 必定满足。容易发现，\(f(i,x) \geq f(i,x+1)-1\)，即 \(f(i,x)\) 的最小值就是 \((i,x)\)。那么 \((i,x)\) 也是不合法的，与原假设矛盾。所以第 \(i\) 行必定全部同时合法或者全部同时不合法。然后归纳就对了，很显然。

现在，只需要找到第一个满足该行第一个位置不合法的行就行了。也就是说，找到第一个满足 \(f(x,1)\geq (x,1)\) 的行就行了。但是实际上，也存在这样一种情况：\((x,y)\) 不合法，但是 \(f(x,y)<(x,y)\)。不过这种情况并不会影响我们计算答案，具体留给读者思考。于是，直接找到第一个满足 \(r\geq \sum\limits_{j=i-u}^{i-1} s_j\) 的位置 \(i\)（还要满足 \(i\geq u+2\)），然后就做完了。带修是容易的。时间复杂度 \(O(2^{\log n}\log n)\)。

G - Sorting Problem Again（已过）

找到第一段有序的前缀和有序的后缀，中间的东西肯定需要排序（除非原序列已经有序）。

但是有可能不止中间的东西需要排序。如果中间的最小值小于这段有序的前缀中的某个值，那么排序的区间还需要再扩大。发现因为这时这个前缀已经有序了，所以想找到该扩大到哪，只需要在原序列上二分就行了。画一下图就能理解。时间复杂度 \(O(n\log n)\)。

我有一个神秘的 \(O(n\log^2 n)\) 做法，据 jr 说能过。

H - Farmer John's Favorite Function（已过）

如果 \(n>6\) 的话，那么 \(f(1)\) 对 \(f(n)\) 的影响只会有 \(1\)。意思是，将 \(f(1)\) 赋值成 \(0\) 的话，算出来的 \(f(n)\) 最多只会少 \(1\)。这启示我们每六个连续的数分一块，对于每一块维护 \(x,y\)，表示如果 \(f(l-1) < x\)，则 \(f(r)=y\)，否则 \(f(r)=y+1\)。发现 \(x,y\) 这样的二元组是可以在线段树 pushup 时合并的，所以直接做就可以做到单次修改+询问 \(O(\log n+\log\log V)\) 的时间复杂度。算 \(y\) 是简单的，算 \(x\) 直接倒推就行了。

当然，\(\sqrt n\) 分块的话不用线段树也能做到 \(O(q\sqrt n)\) 之类的时间复杂度吧。

F - Collecting Stamps 4

确定起始位置后，环变成序列。将某个数的第一个出现位置对应成 \(0\)，第二个出现位置对应成 \(1\)，那么这个序列能带来的不同的 card 就有 \(n^2-s\) 种，其中 \(s\) 是对应出的 \(01\) 串中 10 子序列的数量，证明显然。

每次交换都可以减少一个 10，并且可以证明这是最优的。所以，对于一个询问的 \(K\)，答案就应该是 \(\min_{i=1}^n C_i + \max(0,X(K-(n^2-s_i)))\)。这个式子在算出 \(s_i\) 后是很好维护的。考虑当前起点相比上一个起点，增量是多少。这个增量可以树状数组来算，也很简单。所以 \(s\) 序列也可以 \(O(n\log n)\) 计算。于是这道题就做完了，时间复杂度 \(O(n\log n)\)。

先写下代码再更新。

A. Anti-Plagiarism

题意：有一棵点数为 \(n\) 的树 \(T_1\)，还有一棵点数为 \(m\) 的树 \(T_2\)（保证 \(m\leq n\)）。需要回答 \(T_2\) 是否是 \(T_1\) 的一个连通子图（点可以任意标号）。

设 \(dp_{u,a,b}\) 表示，\(T_2\) 上的以点 \(u\) 为根的子树是否能和 \(T_1\) 上的以点 \(b\) 为根的子树匹配，其中认为 \(a\) 是 \(b\) 在 \(T_1\) 上的父节点，且 \(a,b\) 需要相邻。

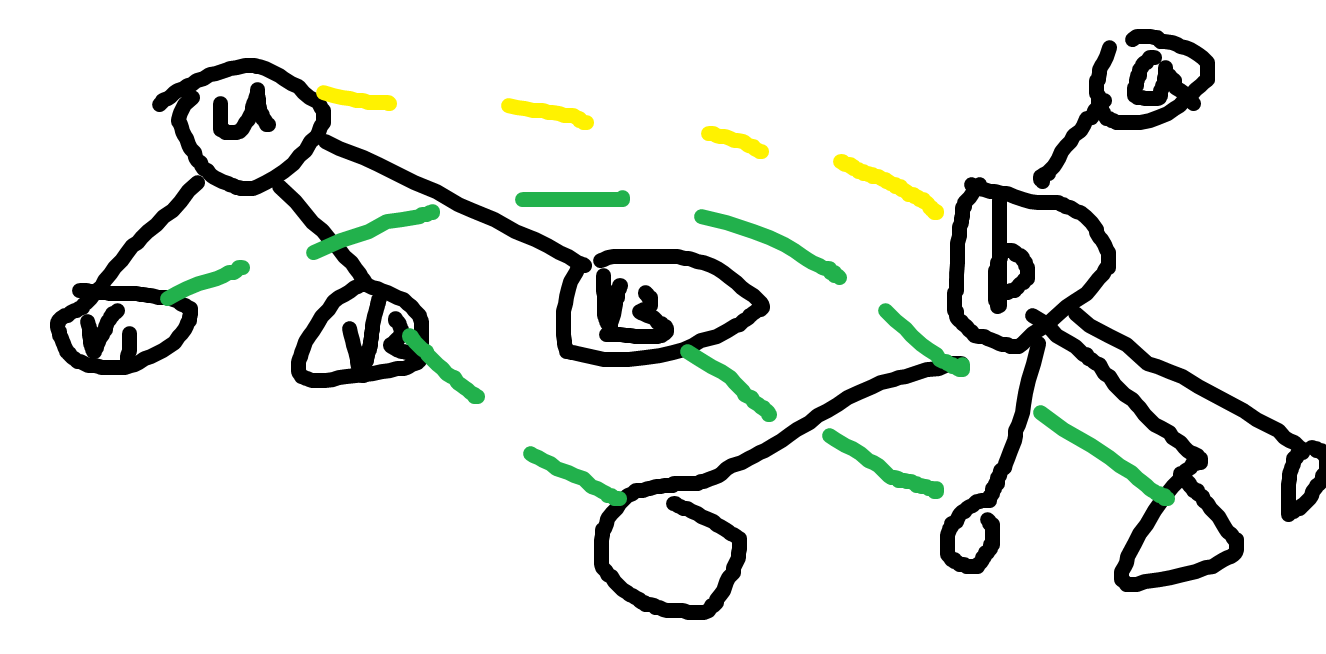
大概就是这么个情况，我们需要将 \(u\) 的所有子节点和 \(b\) 的所有子节点匹配。当且仅当 \(u\) 的某个儿子的子树和 \(b\) 的某个儿子的子树能匹配时，这两个子节点才能作为子节点匹配。这里就会用到已转移过的 DP 值。

这显然是个二分图匹配，只用看 \(u\) 的子节点那边有没有满流就行了。可以跑 Dinic。虽然 DP 的状态数显然是 \(O(nm)\) 的，但是这里跑 Dinic 的点数可能非常多（如果 \(T_1\) 是个菊花就爆了）。所以这个朴素做法是过不去的。

不过发现，当 \(u\) 和 \(b\) 固定时，\(a\) 的变化只会在二分图中删一个点再加一个点。那么现在我们就把 \(u\) 所有的子节点放在左边，把 \(b\) 所有的邻居放在右边（包括 \(a\)），然后跑二分图匹配。如果右边满流了，那么显然所有 \(a\) 的 DP 值都应该是 true。
不对。嗯嗯？？
完了。谔谔。
第三炸弹 · 败者食尘。让我们把时间回退到“所以这个朴素做法是过不去的。”

这个做法实在是太没有前途了！！！设 \(dp_{u,a,b}\) 表示，\(T_1\) 上的以点 \(u\) 为根的子树是否能和 \(T_2\) 上的以点 \(b\) 为根的子树匹配，其中认为 \(a\) 是 \(b\) 在 \(T_2\) 上的父节点，且 \(a,b\) 需要相邻。你肯定能发现这个状态改变了什么。虽然不太直观，但是这样做也是对的。而且更重要的是：我们可以优化了。

当 \(u\) 和 \(b\) 固定时，\(a\) 的变化只会在二分图中删一个点再加一个点。那么现在我们就把 \(u\) 所有的子节点放在左边，把 \(b\) 的所有的邻居放在右边（包括 \(a\)），然后跑二分图匹配。如果右边满流了，那么删去任意一个 \(a\) 肯定还能满流，也就是说所有 \(a\) 的 DP 值都应该是 true。如果右边有至少两个点没匹配到，那么删去任意一个 \(a\) 肯定还是不能满流，也就是说所有 \(a\) 的 DP 值都应该是 false。现在只剩下一种情况了，然后参考一下题解吧，谔谔。

总而言之，如果现在固定了 \(u\)，对于所有的 \(b\)，总共需要跑的 Dinic 点数是 \(O(md_u+m)\) 的。然后就是，对于所有的 \(u\)，需要跑的 Dinic 总点数就是 \(O(nm)\) 的。所以总时间复杂度 \(O(nm\sqrt {nm})\)。不对不对，分析得不好。

\(O(\sum\limits_{u\in T_1}\sum\limits_{v \in T_2} ((d_ud_v)\sqrt{d_u+d_v})\)。

我只会分析 \(O(nm\sqrt n)\)。为什么是 \(O(nm\sqrt m)\)？？？会的人私信我。

QOJ#4489. Multiply 2 Divide 2

考虑一个比较一眼的贪心算法。从左往右扫，每次把当前这个数 \(\times 2\)，直到它不小于前面那个数。
显然这个算法是错的。具体地，假设 \(a_i\) 已经大于 \(a_{i-1}\)，那么我们可能有如下两种决策：

• 把 \(a_i\) 变小。这样可能能让后面的数乘的少一些，从而减少操作次数。
• 让 \(a_i\) 不变。可能比上一种情况更优。

一旦出现这样的情况，贪心算法的正确性就不能保证了。不过这给了我们一些启示：若 \(a_i\) 操作后已经大于 \(m\) 了（\(m\) 为值域上限），那么从 \(i+1\) 开始贪心就是对的。因为不可能出现刚刚那种后大于前的情况。

先不管这个结论。考虑朴素 DP。设 \(f_{i,j,k}\) 表示第 \(i\) 个数被变成 \(\lfloor \frac{a_i}{2^j}\rfloor2^k\) 且 \(a_1\sim a_i\) 递增时所需的最小操作次数。这个状态显然是对的。转移就是找到一对 \((j',k')\)，满足 \(\lfloor \frac{a_i}{2^j} \rfloor 2^k \leq \lfloor \frac{a_{i+1}}{2^{j'}} \rfloor 2^{k'}\)，然后 \(f_{i+1,j',k'} = \min(f_{i+1,j',k'}+f_{i,j,k}+j'+k')\)。

注意到若把所有 \((j,k)\) 二元组按 \(k-j\) 为第一关键字从小到大排序，按 \(j\) 为第二关键字从大到小排序，那么 \(\lfloor \frac{a_i}{2^j} \rfloor 2^k\) 必定不降。

证明（感谢 wxir，wxr_ 等人提供思路）：把 \(a_i\) 看作一个二进制数，把除以 \(2^j\) 下取整看作右移 \(j\) 位，把乘以 \(2^k\) 看作左移 \(k\) 位，那么观察最高位的变化就能发现第一关键字的排序方式是对的。第二关键字的排序方式显然也是对的，因为右移越多就相当于舍弃了越多低位的值，即使高位的值一致。然后它就显然是对的了。

所以这个转移可以双指针做到均摊 \(O(1)\)。状态数是 \(O(n \times \log m \times \text{idk})\)，其中 \(\text{idk}\) 意为 \(\text{I don't know}\)。

不过根据刚才的性质，一旦 \(a_i>m\)，我们就可以直接贪心了！也就是说，这里的第三维只有 \(O(\log m)\) 的级别。于是这一部分的复杂度就是 \(O(n\log^2m)\)。

预处理贪心的结果也是简单的，设 \(g_{i,j}\) 表示第 \(i\) 个数是 \(\lfloor \frac{a_i}{2^j} \rfloor 2^x\) 时，让后面递增需要的最小操作次数。其中，\(x\) 的值是最小的满足 \(\lfloor \frac{a_i}{2^j} \rfloor 2^y > m\) 的 \(y\) 的值。转移是简单的。

总而言之，反正就能做到总而言之的言而总之的 \(O(n\log^2 m)\) 的总而言之的言而总之的复杂度了，言而总之。

H - Kuroni and Antihype

其实这个题才是整个图论专题里最有价值的题。

如果 \(a_u \text{ AND } a_v=0\)，就可以连接两条单向边：\((u,v,a_u)\)（表示 \(u\) 邀请 \(v\)），\((v,u,a_v)\)（表示 \(v\) 邀请 \(u\)）。然后这相当于一个最大树形图问题。但是我不会做，所以可以参考这个。

不过因为边数起飞了，所以不能直接上最大树形图。注意到一些性质：边权只和点权有关。我们可以在一开始就把边权设成 \(a_u+a_v\)，而且把它看成无向边。这样的话，我们只会在原最大树形图上每个点作为儿子时多算一次它的点权。

惊人的观察：每个点只会当一次儿子！！！（即它最多只有一个父节点。）

所以算多的可以直接减去。不过这样的话根节点会被多减一次（根节点不会作为儿子）。所以对于每一个连通块，我们必须钦定一个根节点将它的点权加回来。也就是加上当前连通块的最大点权。但是如果答案就这样计算的话，可能会出现故意不连接某条边让连通块数量增多，从而让加的点权变大的情况，这样就不能简单地使用 MST 了！！！

题解做法非常地聪明，增加了一个点权为 \(0\) 的虚点，并且在一开始就无偿加入。这样的话，选根这一步就会自动选好，并且容易发现，原来无偿加入的点现在会因为这个虚点加入，那么贡献就是虚点的点权，也就是还是 \(0\)。所以它就是对的。

于是现在只需要求 MST。显然使用 B \(\text{什么}\) ka。

不过还有一个 \(O(3^{18} \alpha(n))\) 的做法。因为对于每条边来说，\(a_u \text{ AND } a_v=0\)，所以边权 \(a_u+a_v\) 实际上就等于 \(a_u \text{ OR } a_v\)。如果这样的话，我们就可以枚举一条边权（从大到小），然后枚举其子集，得到合法的 \((a_u,a_v)\) 对，然后用并查集合并（即 Kruskal）。如果没有按位与值为 \(0\) 的限制，我们就必须枚举所有 \(\leq w\) 的 \(a_u\)，复杂度就炸了。不过现在有这个限制，所以可以只枚举子集。于是复杂度就是对的了。

对于权值相同的点，我们需要一起考虑。设 \(siz_i\) 表示，在以 \(i\) 为根的并查集树上所有点的权值在原图上形成的连通块个数，然后随便算算贡献就行了。合并的时候也可以随便维护。显然是对的。

A - Following Arrows

跟着箭头。

一般来说，这种题我们会考虑构造出所有 \(2\) 的幂次再组合。

先考虑 \(1\times M\) 的情况，最劣情况是全填 L，发现这样也只有 \(O(M^2)\) 步。因此上述构造看起来不太可行。

重新考虑 \(1\times M\) 的情况，发现每个网格贡献独立。（因为第一次走到该格子时前面格子状态已确定。）所以理论上我们可以构造出 \(\geq M-1\) 的任何一种步数。（当然要小于等于上界。）

现在将构造扩展到二维。

怎么开始讲 B 了。

B - Heuristic Knapsack

启发式背包。

Alice 很好，因为她能取到的物品集合是一段前缀。枚举 Alice 能取到的前缀（先只考虑体积确定的物品）。那么我们想让前缀内的物品被 Bob 取到，前缀外的不被 Bob 取到。于是前缀内的物品价值设成 \(10^9\)，前缀外的物品价值设成 \(0\)。这是一个简单的贪心。

再转换到 Bob 的视角。

没听懂。

】】】】】】【【【【【【【【】】】】】】】】【【【【【】】】】】】

D - Pointless Machine

缺点机器。

问 \(1\sim n\)，问 \(n\sim 1\)，就可以知道度数了。然后我们就可以剥叶子！记录每个点邻居的编号异或和！G75兰海高速！垃圾题。

先枚举某一位，然后尝试求出每一个点周围这一位为 \(1\) 的点有多少个。这个怎么做？

\(k\log_k n\) -> \(e\) -> \(3\log_3 n\)。\(k\) 叉分治 -> 多叉分治。

D. Interesting Counting Problem

考虑一个普通の树形背包。
如果每个物品の体积都是 \(1\) 的话，我们就可以轻松地做到 \(O(n^2)\) 或者 \(O(nm)\) の复杂度。

这文章写得也太好了，一点都不现充。

但是如果每个物品の体积可以达到 \(m\)，我们貌似就只会做 \(O(nm^2)\) 了。非常不好。为什么呢？因为合并两个背包的复杂度实在是太高了！如果我们每次只加入 \(1\) 个物品，共加入 \(n\) 次，就可以轻松地做到 \(O(nm)\)。

不对，这个东西好像做不了。已蕾姆。已Reimu。

不对，我在说啥呀。这个东西就是普通的 01 背包。跟树的形态一点关系都没有。直接做就是 \(O(nm)\) 的。举例举错了。反正就是，这个做法能把树上依赖背包优化成 \(O(nm)\)，虽然我也没讲这个做法具体是什么，哈哈哈。哈。（哈哈哈哈。）

不管了，我们直接来看这个题。

这个题我们只需要求根节点的答案，但是节点与节点之间有一些依赖关系。具体的，一旦我确定一个点填 \(0\)，那么在之后的转移中，就不需要考虑它的子树了。（这个后面会讲。）

我们设 \(dp_{i,j}\) 表示已经考虑完 dfn 序前 \(i\) 小的点后，当前连通块体积为 \(j\) 时的答案。考虑下一个点填的数。（这里点已经按照 dfn 序重标号了。)

• 下一个点填 \([1,R_i]\) 中的每一个数。可以转移到 \(dp_{i+1,(j+v)\bmod m}\)，其中 \(v\) 是当前枚举的下一个点填的数。这个显然可以前缀和优化，并且只有两种不同的系数。总而言之就可以 \(O(m)\) 转移。

• 下一个点填 \(0\)。设 \(f_v\) 表示只考虑 \(v\) 这棵子树，包含 \(v\) 的连通块大小是 \(m\) 的倍数时的方案数。这种转移下，整个 \(i+1\) 的子树都不用考虑了，因为必须满足它所有的儿子所在连通块大小都是 \(m\) 的倍数。如果普通转移但是不钦定它儿子的体积的话，就会算到不合法的方案。如果钦定了系数为 \(\prod_{v\in son_{i+1}} f_v\) 但还是普通转移的话就会算重。（而且还会算到不合法的。）所以我们的不用考虑指的是可以直接转移到 \(dp_{i+siz_{i+1},j}\)。也就是直接跳过 \([i+1,i+siz_{i+1}]\) 这个区间，即 \(i\) 的子树区间。系数就为 \(\prod_{v\in son_{i+1}} f_v\)。这个跳过显然是对的，不再啰嗦。时间复杂度 \(O(m)\)。

看起来就做完了。但是发现这样的 DP 我们其实要做 \(n\) 遍。因为 \(f\) 数组也是通过 \(dp\) 转移出来的，而且为了求出 \(f\) 数组，我们需要的显然是一个子树的 DP 值，如果直接拿全局来算的话，那就不是一个子树的 DP 值了。

这个怎么办？？？发现一个点的 DP 值可以从儿子那里继承。继承过来过后再挨个加入子树中其它节点，然后最后加入当前节点。加入当前节点时也有两种转移。然后显然就是对的了。然后显然继承重儿子复杂度就能做到 \(O(nm\log n)\)。然后就做完了。

P11567 建造军营 II

先刻画一下 \((p_i,q_i)\) 的性质。（若无特殊说明，以下的路径指的都是可以经过重复点但不能经过重复边的路径。）

Lemma 1：在一个边双连通分量内的任意两点间必定存在两条边集不交的路径。

证明：如果不存在这样的两条路径，说明有一条边必定在两点间的路径上。那么它就是割边，矛盾。

Lemma 2：在同一个边双连通分量中，\((u,v)\) 之间的全部路径并必定是整个边双连通分量的边集。

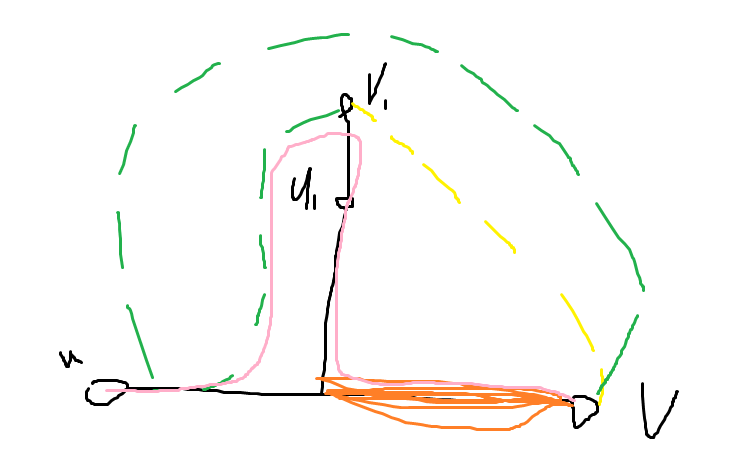
询问 Deepseek 后无果，遂口胡一下。有误请指出。现在我们想找到一条 \((u,v)\) 之间的路径覆盖边 \((u1,v1)\)。假设我们已经沿黑色路径从 \(u\) 走到了 \(v1\)。\(v1\) 和 \(v\) 之间必定存在一条路径，但我们不能沿着其走回来。根据 Lemma 1，肯定还存在一条与这条路径不交的路径。让我们分类讨论。

• 这条路径与 \(u\) 到 \(v1\) 的路径不交。

即存在一条黄色部分的路径，这种时候可以直接走到 \(v\)。

• 这条路径与 \(u\) 到 \(v1\) 的路径有交。

即存在一条绿色部分的路径。这种时候可以在从 \(u\) 到 \(v1\) 时不走黑色部分的路径，而去走必定存在的一条粉色部分的路径。显然也满足条件。

于是我们就证明了任意一条 \((u1,v1)\) 的边都能被覆盖到。

Lemma 3：把边双连通分量缩点后形成边双树，若存在 \((p_i,q_i)\) 的限制，则边双树上 \(p_i\) 所在边双到 \(q_i\) 所在边双全部要驻守军队。（包括边和边双。若边双需要驻守军队，指的是该边双里的边全部需要驻守军队。）

根据 Lemma 1 和 Lemma 2 可以轻易证得。

根据 Lemma 3，我们会发现此题跟边双有很大关系。显然需要求 \(f_S\) 表示 \(S\) 形成一个边双的方案数。（即只保留没有被焦土行动的边。）然后再考虑后续驻守军队。

那么这个东西怎么求呢？先求出 \(g_S\) 表示 \(S\) 连通的方案数。这是好求的，随便容斥即可。求 \(f_S\) 也可以容斥：先求出连通的方案数，再减去边双树节点个数 \(\geq 2\) 的图即可。

于是设 \(h_{S,i}\) 表示，点集 \(S\) 连通，且边双树上有 \(i\) 个节点时的方案数。设当前考虑到了 \(S\)，我们可以通过这种方式求出 \(h_{S,i}\)（对于所有 \(i\geq 2\)）：

\(h_{S,i}=\sum\limits_{T\subset S,T\neq S,T\neq \varnothing,1\leq j < i} h_{T,j}\times h_{S-T,i-j} \times E_{T,S-T}\)。

然后显然 \(f_S= g_S - \sum\limits_{i=2} h_{S,i}\)。再把 \(h_{S,1}\) 赋值成 \(f_S\)，然后继续转移，这样就是对的了。这样显然是错的。因为计算 \(h_{S,i}(i\geq 2)\) 时会算重。这相当于我们计数一棵树的时候从每条边断开时计算了一次，并且不同的方向也计算了一次（即一个连通块在作为 \(T\) 时会计算一次，并且在作为 \(S-T\) 时会计算一次），所以会算重 \(2i-2\) 次。所以需要把 \(h_{S,i}(i\geq 2)\) 除以 \(2i-2\) 后再拿去转移。时间复杂度 \(O(3^n n^2)\)。优化暂时不会。

观察边双树的形态，发现其一定是由若干个极大黑色连通块和白色边双由白边连接而成。（这里，黑色指的是我们用 \((p_i,q_i)\) 的限制让其必须驻守军队，白色指的就是没有让它必须驻守，但是这并不妨碍我们往白色边上驻守军队，需要区分开黑/白和驻守/不驻守军队，不然后面的东西会很难理解。）

抑郁症。

设 \(B_S\) 表示 \(S\) 形成一个极大黑色连通块的方案数。我们钦定 \(|S|=1\) 时 \(B_S=1\)。因为一旦一个 \(S\) 中没有任何限制，这样就可以将它的方案数算成 \(0\)。而且，如果存在一个 \(i\)，满足 \(p_i\in S\) 并且 \(q_i \notin S\) 或者 \(q_i \in S\) 并且 \(p_i \notin S\)，\(B_S\) 就必须为 \(0\)。不然就会出现跨块的限制，显然不合法。

这个怎么转移呢？可以发现刚刚那个边双连通分量计数问题是可以一般化的。我们给了若干边，给了将每个集合变成一个“点”的方案数。然后先把全部点化成若干集合，再在中间连边形成一棵树，求方案数。这个问题也一样。如果一个连通块并不是一个极大黑色连通块，那么它一定是若干极大黑色连通块由白边连成的一棵树。然后就也可以容斥了！！！不细说了。

还要求 \(W_S\) 表示 \(S\) 形成一个白色边双连通分量的方案数。而且因为其中的边可以选择驻守/不驻守军队，所以还有一个 \(2^m\) 的系数，其中 \(m\) 是边双的边数。这个可以沿用 \(f\) 的转移，然后带个系数就行了。如果存在 \(p_i \in S\) 或者 \(q_i \in S\)，\(W_S\) 就必须为 \(0\)，原因显然。

最后，要 DP 这个边双树。现在其实每个极大黑色连通块和白色边双可以看作是本质一样的，因为它们都由白边连接。那么处理一个集合 \(A_S\) 表示 \(S\) 这个集合是边双树上的一个点时的方案数（我们将一个极大黑色连通块也看作一个点！！！），它显然等于 \(W_S+B_S\)。只有在 \(|S|=1\) 时，我们要将其特殊处理成 \(1\)，原因显然。然后再跑一个我们一般化后的问题就做完了。时间复杂度 \(O(3^n n^2)\)。还要处理边上的 \(2\) 的权值，差点忘了。

怎么优化？？？？？？？？？？我不会，会的人私信我。

Andyjzy 会了！！！

观察发现，复杂度瓶颈在这里。

\(h_{S,i}=\sum\limits_{T\subset S,T\neq S,T\neq \varnothing,1\leq j < i} h_{T,j}\times h_{S-T,i-j} \times E_{T,S-T}\)。

我们居然一边在做子集卷积，一边在做加法卷积，这样非常不好！因为一个点集对应的 \(h\) 可能被它的超集用到多次！（去做加法卷积。）我们将每个 \(h_S\) 看作一个多项式，那么总共只有 \(2^n\) 个多项式，所以将其全部暴力转成点值的复杂度是非常低的，仅仅需要 \(O(2^n n^2)\) 的复杂度。于是，每个 \(h_S\) 可以一起求。只需要枚举 \(T\)，然后将 \(T\) 与 \(S-T\) 的点值相乘，得到若干多项式对应点值，再将这些点值用 \(O(n)\) 拉格朗日插值求出系数，对不同的多项式乘上不同的 \(E_{T,S-T}\)，再对应相加就可以了。发现只需要做 \(O(3^n)\) 次 \(O(n)\) 拉格朗日插值，于是时间复杂度是 \(O(3^n n)\) 的，就过了，常数飞起，很难写，蕾姆。

不对啊。谁会 \(O(n)\) 连续点值转系数？我没招了。

哦哦，我知道了，后面和 \(x\) 有关的东西因为只和 \(x\) 有关所以可以直接预处理出来，反正意思就是说我们取的点值对于每一个多项式来说横坐标都是一样的，所以随便搞一搞就可以了。有点抽象。

这能写吗？

A - 春节十二响

考虑菊花，考虑双链。子树中已经分好的段可以看作一个点上连下去了若干条链，因为我们不会再让子树间的段合并。所以可以从下往上合并。从大往小排，两两合并。

B - Serval and Colorful Array (Hard Version)

经典问题：\(k\) 个人在一个长度为 \(k\) 的连续区间里集合，求走的距离和最小。第 \(i\) 个人的初始位置是 \(a_i\)，不存在两个不同的人初始在同一个位置。连续区间的左端点不确定。设其为 \(x\)，则答案为 \(\sum\limits_{i=1}^k |a_i-(x+i)|\)。因为 \((a_i-i)\) 单调，所以 \(x\) 选中位数最优。

不过现在我们 \(a_i\) 也没确定，\(x\) 也没确定。所以想保证 \(x\) 是中位数其实很难。不如直接设 \(f(a,x)=\sum\limits_{i=1}^k |a_i-(x+i)|\)，那么答案就是 \(\min\limits_a\min\limits_{x=1}^{n-k+1} f(a,x)\)，交换枚举顺序，发现可以变成 \(\min\limits_{x=1}^{n-k+1}\min\limits_a f(a,x)\)。现在枚举 \(x\)，那么答案直接就是它到最近的 \(1\) 到 \(k\) 的距离之和。这个显然是对的，我们不要求其是中位数了，这是因为如果对于我们找到的 \(a\) 序列来说它不是中位数，那么答案一定会在真正的中位数那里更优。也就是错解不优思想。

这个东西怎么算呢？可以直接算 \(a\) 序列对每个 \(x\) 的贡献。对于同一种数的两个相邻出现位置，这种数对这两个出现位置之间的 \(x\) 的贡献是两个等差数列的拼接。于是直接二阶差分就做完了。

为啥要枚举左端点啊？还带个 \(i\) 的贡献。直接枚举最后集合区间的中点不就直接做完了。

C - Skyscape

构造专练。可以看成交换了若干次相邻逆序对。考察该操作性质，发现原序列的顺序对在操作后的序列中仍是顺序对。再考察一下，发现只要满足序列 \(A\) 和序列 \(B\) 满足上述性质，那么就一定能通过题目所给的 \(n\) 次操作转化。这是充要的。

构造。先判断已经确定的数。有两种限制：空位和确定位置，空位和空位。\(x\) 能填在哪些空里面。发现其必定是一个区间。数和区间匹配，完美匹配，直接贪心！非常经典。

但是还存在新填的数和新填的数之间的限制。\(r_x\leq r_y\)，\(l_x\leq l_y\)。先填 \(x\) 再填 \(y\)。一旦存在 \(x\leq y\leq z\)，且 \(z\) 是一个确定的数，那么 \(z\) 带给 \(y\) 的限制同样会带给 \(x\)。因此，能得到 \(r_x\leq r_y\)。同理，也能得到 \(l_x\leq l_y\)。也就是说，只要正常地去填，\(x\) 一定比 \(y\) 先加入，并且 \(x\) 一定比 \(y\) 先弹出，那 \(x\) 在我们构造的序列中的位置就一定会 \(y\) 在该序列中的位置，所以这个限制是自然满足的。如果有 \(r\) 相等的情况判一判 \(l\) 就行了。

\([l,r]\) 完全相同怎么办？可以按 \(x,y\) 本身的值排序。

D - Iris and Adjacent Products

因为只存在相邻的限制，所以翻转是一个很好的验证性质的操作。不过这题的结论比较好猜就是了。

\(cnt_{>\frac{k}{x}} \leq cnt_{\leq x}\)，有一点 corner case。这是充要的，构造即为最大 最小 次大 次小 ...。会有一点 corner case（末尾情况）。所以呃大概我们需要做的事情是就我们会我想想就是大概像这样就对吧大概是我们是可以这样填的这种时候。每次修改操作，\(cnt_{\leq}\) 会增加 \(1\)，\(cnt_{>}\) 会减少 \(1\)。还有 corner case。对于每个 \(x\) 离线地求，因为答案是所有 \(cnt\) 之差的什么东西求 \(\max\)，所以可以做到空间复杂度线性。

E - Distinct Elements on Subsegments

构造专练。\(B\) 的相邻位置最多差 \(1\)。若刚好差 \(1\)，则知道两端在中间的出现情况。相等就有两种可能，要么不变，要么右边 \(+1\)，左边 \(-1\)。

限制条件形如，一个数需要在前面/后面的 \(k-1\) 个数里出现/没出现过。若存在一个数相邻两次出现距离 \(\geq k\)，则可以前面拆成一个数，后面拆成一个数，答案不会有影响。因此，限制变为：

• 前/后有/没有相同的数。
• 一种数出现的相邻两次距离差 \(<k\)。

匹配是显然的。直接贪心！呃，我想想应该怎么说呢就是呃应该是说它们两个事实上是可以誒就是或者说我们应该说它们两个数一定是可以相等的看看能理解意思吗就是它们两个数就是

嗯？Slow or no Internet.怎么回事？不应该啊？（听不清）那我们只能用画图了。（台下观众笑。）

\(\leq k-1\) 的限制 -> \(\leq k\)，不影响答案。能加即加。开头 \(B_1\) 个点没有入度。有入度的点越靠后越好。两个相等的情况，分类讨论。我思考一下这边呃但我觉得这样也不一定需要这样这个这个特判好像是不需要的。没听懂。那这样的话我我我我我好像不太需要判这种 \(B=1\) 的情况。（4327 Byte）好像我根本没判啊。

为啥没讲不存在的条件怎么做？

H - Doubles Horseback Wrestling

怎么这么卡。当前合法的最差的点，拿它先去匹配，这是很多贪心题最优的策略。如同每个点匹配一段区间时，就会采用这种做法。这道题也是一样的。\(l2\leq s-l1\)，\(r2\leq s-r1\)。很有道理啊！！！

构造倒水

先考察 \(b_i = 1\) 的做法。

想一想能得到两个简单做法。（设 \(a\) 中非零数数量为 \(A\)，\(b\) 中非零数数量为 \(B\)。）

做法一

把所有数倒到 \(n\) 的位置，然后从 \(n\) 开始不断往下流。操作次数 \(A+n-1\)。

做法二

以 \(1\) 作为中转位置。若 \(1\) 开始有水，就将其分给任意一个没有水的位置。否则让一个有多余水的位置 \(u\) 把水分给没有水的位置 \(v\)。进行两次操作即可：\((u,1),(1,v)\)。操作次数 \(2(n-A)\)。

这里平衡一下就可以做到 \(\lfloor \frac{4n}{3} \rfloor\) 了。若 \(A\leq \lfloor \frac{4n}{3} \rfloor -(n-1)\)，则使用做法一。否则做法二操作次数为最多为 \(2(2n-\lfloor \frac{4n}{3} \rfloor -2)\)。对余数分讨一下就可以证明其 \(\leq \lfloor \frac{4n}{3} \rfloor\) 了。

若 \(b_i\neq 1\)，可以用前两个做法先将其变成 \(b_i=1\)，再暴力把 \(b_i=1\) 的状态合并。那么每种做法会加上 \(n-B\) 的操作次数。（因为有 \(n-B\) 个位置要给出自己仅有的一单位水。）

因此，做法一 Plus 操作次数为 \(2n+A-B-1\)，做法二 Plus 操作次数为 \(3n-2A-B\)。

但是还是过不了，考虑一个做法三。

做法三

先把所有水倒到 \(n\) 中，然后从大到小枚举 \(i\)。若 \(b_i > 0\)，就将 \(n\) 中的水倒入 \(b_i\) 中再倒给 \(i\)。操作次数为 \(A+2B\)。

这三个东西最小值怎么算？？？操作次数加起来发现刚好为 \(2n+A-B-1+3n-2A-B+A+2B\) 即 \(5n-1\)。于是三种做法的操作次数不可能都大于 \(\lfloor \frac{5n-1}{3} \rfloor\)。然后就做完了。

Boring Counting Problem

考虑 \(k=2\) 怎么做。简单思考一下，发现一个连通块包含的颜色二元组的可能性只有 \(O(n)\) 种。因为它要么是一个单点，要么至少包含一条边。根据这条边端点的颜色，我们就可以确定整个连通块包含的颜色二元组。

那么可以设计状态 \(dp_{u,j}\) 表示，当前这个连通块仅包含点 \(u\) 的颜色和颜色 \(j\) 时的方案数，其中颜色 \(j\) 必须在 \(u\) 的邻居中出现过。这个状态数显然是 \(O(n)\) 的。不过状态设两维还是太不优雅了。我们设 \(f_u\) 表示钦定 \((u,p_u)\) 删除时，\(u\) 子树的删边方案数，\(g_u\) 表示钦定 \((u,p_u)\) 保留时，\(u\) 子树的删边方案数。（显然，树上的连通块划分方案数和删边方案数是等价的。）

转移即为：

\(f_u = \sum\limits_{C=1}^n (\prod\limits_{v\in Son_u}(f_v+[c_v=C]g_v)-\prod\limits_{v\in Son_u}f_v) + \prod\limits_{v\in Son_u}f_v\)。

\(g_u = \prod\limits_{v\in Son_u}(f_v+[c_v=c_{p_u}]g_v)\)。

最后答案显然就是 \(f_1\)。转移可以用一些手段做到 \(O(n)\)。（真的吗？事实上我只会 \(O(n\log n)\)。wxir 骗我。）

当 \(k=3\) 时，就比较复杂了。先考虑 \(f_u\) 的转移，若 \(u\) 所在连通块只有两种颜色，那就可以沿用刚才的转移。但如果有三种颜色的话，就必须再维护一个东西 \(h_{u,j}\) 表示钦定 \((u,p_u)\) 保留，且 \(u\) 所在连通块还有颜色 \(j\) 时的方案数才能转移。具体地，枚举这两种颜色：

枚举啥呀。不会。

当你紧张时，就你的对手他可能也在紧张。—— \(\mathbb{H}\) 之神。
如果你问常数在 noi 真的有用吗，真实情况就是常数更小，就算复杂度不对也能冲过去。所以还是有必要的。—— 大 \(H\)。

Good Counting Problem

Bad Counting Problem

Best Counting Problem

Another Counting Problem

Yet Another Counting Problem

物品分类

\(type=1,2,3\) 是 EASY 的。直接猜猜结论统计一下就做完了。如果只有这三个 \(type\) 完全可以放达摩院模拟赛 T1。

\(type=4\) 是 HARD 的。考虑如何去简单地刻画 \(g(p)\)，从而让其能够被计数。这是 HARD 的，但是我们还是能发现 \(g(p)=len(p)-cnt(p)-[cnt(p)=len(p)-1]\)。其中 \(cnt(p)=\min(L_p,R_p)\)，其中 \(L_p\) 为 \(p\) 最长的元素互不相同的前缀的长度，\(R_p\) 为 \(p\) 最长的元素互不相同的后缀的长度。这是相当不显然的，\([L_p+1,len(p)]\) 显然是一个合法的垃圾子序列对应的子串，因为 \(p\) 中的第 \(L_p+1\) 个元素是第一个在前缀中重复出现的元素，而且还能知道不存在一个更长的后缀满足它很垃圾。同理 \([1,len(p)-R(p)]\) 也是一个合法的前缀。（我们显然可以证明一个对应的子串不是前/后缀的垃圾子序列一定不是最长的。）然后显然那个表达式就是对的了，不再赘述。

所以现在要统计 \(\sum len(p)\)，\(\sum cnt(p)\) 和 \(\sum [cnt(p)=len(p)-1]\)。式 \(1\) 和式 \(3\) 都是好做的。主要来考虑式 \(2\)。对每个子序列直接算 \(cnt(p)\)？枚举 \(cnt(p)\) 然后统计方案数？发现这个东西 とても HARD！（ハヅ！）不过统计 \(\geq cnt(p)\) 的方案数看起来就比较简单了，因为不需要满足它恰好了。

具体地，枚举 \(p\) 的第 \(k\) 个位置 \(l\) 和其倒数第 \(k\) 个位置 \(r\)。假设 \(l\leq r\)，那么只需要满足 \(l\) 左边选择了 \(k-1\) 个不同的，\(r\) 右边选择了 \(k-1\) 个不同的就能保证 \(cnt(p)\geq k\) 了。对于每一个 \(k\) 计算这种方案数再加起来就是答案。这是一个经典的反演。中间选择的方案数就是 \(2^{r-l-1}\)。需要处理的只有 \(F(l-1,k-1)\) 和 \(G(r+1,k-1)\)，分别表示 \([1,l-1]\) 中选择 \(k-1\) 个不同元素的方案数和 \([r+1,n]\) 中选择 \(k-1\) 个不同元素的方案数。发现可以直接预处理 \(F_{i,j}\) 和 \(G_{i,j}\)，使用背包。相当于我有若干个体积为 \(1\)，方案数为 \(cnt\) 的物品（表示选择哪一个），然后统计体积为 \(j\) 时的所有方案。不过假设现在要加入一个物品，它对应的方案数（即出现次数）可能改变，这个时候直接暴力重新插入，反正每个前缀只有 \(O(n)\) 个物品，时间复杂度 \(O(n^3)\)。需要保证加入的元素和 \(a_{i+1}\) 不同。（我们定义一场比赛里有宝藏题目和垃圾题目，发现这个题就是垃圾题目。）

如果 \(l>r\)，就非常的魔怔。魔怔啊！魔怔。魔怔啊！魔怔。从刚刚那种情况可以看出，问题已经和 \(k\) 本身无关了。现在 \(l\) 和 \(r\) 将原序列分成了三段，那么我们其实只需要统计段 \(1\) 和段 \(3\) 选择物品数量相同的方案数！此时一个物品变成了一个分组背包！对的。怎么回滚？

咕咕嘎嘎！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！

垃圾题目！！！！

从这个题目中，我学习到了一个东西。若当前有若干体积为 \(v_i\) 权值为 \(w_i\) 的物品，定义一个物品选择方案的权值为所有选择物品权值的乘积，求所有体积为 \(j\) 的物品选择方案的权值之和。这个东西用背包做显然可以做，而且更重要的是：它可以支持删除任意一个物品！

具体理解方式是，这个背包的生成函数显然是 \(\prod (1+w_ix^{v_i})\)，删掉一个物品就是除以一个式子，显然可以做，而且是线性的，直接递推一下就行了。（可能带 \(\log\)。）

An Unsure Catch

当我们有 \(k\) 次操作机会时，容易发现只有以下两种操作方案有用。（以下可能用“树”简称“基环树”。）

• 选择一个基环树个数为 \(k\) 的基环树集合，用 \(k-1\) 次操作将 \(k-1\) 棵基环树连在剩下的一棵上，再用一次操作将剩下的一棵基环树上的环变成自环，答案为所选集合的节点个数。（显然选前 \(k\) 大的基环树是最优的。）

• 选择一个基环树个数为 \(k+1\) 的基环树集合，用 \(k\) 次操作将 \(k\) 棵基环树连在剩下的一棵上。

第一种操作方案是容易计算答案的。主要考虑第二种操作方案。假设那棵中心树的环长为 \(L\)，该怎么计算答案？

发现一件事情，如果钦定了基环树的根，并将根的连边连到另一棵树上，那么可以将这个基环树看作一个普通的树。对于一棵普通的树，它 \(\bmod L\) 的答案是容易计算的，直接维护深度的桶就可以了。然后，由于可以将当前这个根连到环的任意一个节点上，那么桶中每一种余数都是可以取到的！也就是只要取最大值就行了。举个例子，若树 \(A\) 最大的余数是 \(1\)，出现了 \(3\) 次，树 \(B\) 最大的余数是 \(3\)，出现了 \(2\) 次，那么一定是存在一种连接的方案，使得把树 \(A,B\) 连到树 \(C\) 上后（树 \(C\) 是基环树），树 \(A,B\) 可以做出 \(2+3=5\) 的贡献，并且同时树 \(C\) 也能做出自己最大的贡献。（我在解释什么。）

于是，当前需要处理：环长为 \(L\) 时每棵树断环后的最大值，每棵树不断环时的最大值。第一个东西，由于环长只有 \(O(\sqrt n)\) 种，所以只要能做到 \(O(n)\) 处理最大值就行了。第二个东西是显然可以 \(O(n)\) 做的（环长固定。）

如果既要枚举根又要暴力算就炸了。不过发现每个点只会对 \((pos+dep+L')\bmod L\) 做贡献，其中 \(pos\) 为离当前点最近的环上点的排名，\(dep\) 为当前点到环的距离，\(L'\) 是偏移量，它只和取的根有关，并且 \(L'\in [0,LEN)\) 都能取到，其中 \(LEN\) 是当前的环长（不是枚举的 \(L\)！）。嗯。如果。是不是。嗯嗯？因为它是整体加 \(1\)，所以对集合最大值并没有影响...?那题解做法是不是复杂了？？？哈哈哈，爆表了！！！

先写一下。

UPD：错了。非常垃圾。假设现在根沿着边走了一步，那么普通的 \(pos\) 会 \(+1\)，但是新的根从 \(LEN\) 变到了 \(1\)，直接减去了 \(LEN-1\)。于是可以对普通的维护一个偏移量，新的根的子树直接暴力改。

A - LED Display Renovation

LED 展示翻新。
看一看题解。

B - Play It by Ear

见机行事。ぜんめずお？？？

这种题肯定要先考虑牌堆固定时怎么做。那么假设现在牌堆固定为 \(p\) 了。

先考虑确定一个操作次数下界：设 \(f_i\) 表示完成前 \(i\) 个任务需要的可能的最少轮数（即理论下界）。

MISSION COMPLETED

有转移 \(f_i=1+\max(f_{i-1},f_j+n)\)，其中 \(j\) 满足 \(a_j=a_i\) 且 \(j<i\)，而且它最大。转移含义显然。当然，如果 \(i\) 是 \(a_i\) 第一次出现，那么转移方程应该变为 \(f_i=1+\max(f_{i-1},pos_{a_i}-n)\)，当然 \(f_0\) 要初始化为 \(0\)。含义显然，\(pos_{a_i}\) 表示当前牌堆里 \(a_i\) 的位置。

如果一直遵循以下的策略，那么 \(f_m\) 的下界是可以达到的：若手中有当前任务需要的牌，直接打出。否则打出后续任务中最晚需要我们打出的那一张牌（当然是手牌）。证明我会，但是你问一下哥哥。

那么现在只需要对所有排列的 \(f_m\) 求和就行了。这也太困难了。考虑固定 \(f_m\)，对满足条件的排列 \(p\) 计数。看似 \(f_m\) 有 \(O(nm)\) 种取值，但是观察发现这个转移可以说是线性的，且牌堆本身只对初始的那几项有影响，这个影响显然是 \(O(n)\) 的，所以 \(f_m\) 的取值也只有 \(O(n)\) 种。

然后确定 \(f_m\) 后，可以直接倒推确定所有 \(f_i\) 的最大值，从而确定所有 \(pos\) 的最大值。但是发现这个事情其实是在统计 \(f_m\leq k\) 时的方案数而不是 \(f_m=k\) 时的方案数，不过这差不多差分一下就行了当然不差分也行反正就是做一做贡献。

直接做就可以做到 \(O(nm\log n)\)。

发现最后 \(pos\) 的上界其实形如 \(\min(2n,k-c_i)\)，因为这个转移是线性的，关于 \(f\) 的上界可以归纳证明一定形如 \(k-c_j\)，然后 \(pos\) 的上界再对 \(2n\) 取个 \(\min\) 就行了。考察对象从 \(m\) 个变成了 \(n\) 个，直接做就能做到 \(O(n^2+m)\)。

C - Cute Young Diagram Counting

可愛い年轻表格计数。
看一看题解。

D - The Echoes of Chronos

柯罗诺斯的回响。

柯罗诺斯（古希腊语：Χρόνος）是古希腊神话中的一位原始神，代表着时间。在《二十四行圣辞》中，为时间神。
看一看题解。

扣1领取特制戒指。
♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂♂

E - Relay Jump（已过）

接力跳。

JUMP JUMP MORE JUMP！

观察！若 \(i\) 从 \(j\) 上跳过去了，\(i\) 的坐标从 \((x_i,y_i)\) 变成 \((x_i+2(x_j-x_i),y_i+2(y_j-y_i))\) 即 \((2x_j-x_i,2y_j-y_i)\)。此时 \(\sum x\) 加上了 \(2(x_j-x_i)\)，\(\sum y\) 加上了 \(2(y_j-y_i)\)。因此，一旦知道 \(\sum x\) 的总增量，就相当于我们知道了 \(\sum_{i=2}^k 2(x_{p_i}-x_{p_{i-1}})\)（\(p\) 是操作序列，相当于 \(p_1\) 从 \(p_2\) 上跳过去了，\(p_2\) 从 \(p_3\) 上跳过去了，\(\dots\)，\(p_{k-1}\) 从 \(p_k\) 上跳过去了。）这显然等于 \(2(x_{p_k}-x_{p_1})\)。而 \(p_1 = s\)，\(p_k\) 就是我们要求的答案，所以显然 \(x_{p_k}\) 是可以直接求出的，因为 \(\sum x\) 的总增量我们是知道的。同理 \(y_{p_k}\) 我们也知道。不过发现这里的 \(x\) 数组和 \(y\) 数组是在动态变化的，但是这并不重要，因为中间变化的都被我们消掉了，而 \(x_{p_1}\) 显然是初始状态，\(x_{p_k}\) 显然是最终状态。又因为保证青蛙位置互不相同，所以这道题就做完了。（青蛙子。）

F - Leo（已过）

六。

小时候看这集11037了。

非常有趣的构造题。但是比较困难。虽然样例解释的图给的比较这什么，但是一个状态显然是可以有多条出边的！

这种黑盒状物的构造题已经遇到很多了，都是要求构造一种操作方案，使其对任意一种初始状态都起效。和交互题的区别在于，我们没有实时返回值，不能随时随地调整策略。这种题的做法大概有两种：

• 让状态逐渐趋于同一，缩小当前可能的状态集合。（如果是要求最后到某种状态。）
• 无论序列本身是什么，我们都能在若干次操作后简单地描述其某个特征。（如果是要求序列中的某个值。当然也可能不是序列。）

这道题就用第二种方法了。

发现 \(\texttt{*}\) 是很烦的。在做 \(\texttt{AND}\) 操作时，它非常垃圾。考虑把它消掉。考虑让每个 \(\texttt{*}\) 被其后面第一个有色位置覆盖。

在若干次基础操作的叠加尝试后，发现了如此状物：\(\texttt{x OR y OR y}\)。若 \(\texttt{x = *}\)，它会返回 \(\texttt{y}\)，否则会返回 \(\texttt{x}\)。于是，相当酷炫的，我们从后往前扫，然后不断做这个操作就能达到我们原先的目标，并且不改变颜色出现的顺序，这里会使用 \(2n-2\) 次操作。

在得到酷炫序列后，可能第三种颜色仍然比较难求，但是第二种颜色是好求的。如果找到了第一种颜色第一次出现的连续段，那么我们就能标记出第二种颜色。通过将这个酷炫序列一直做 \(\texttt{AND}\) 操作，我们可以标记出第一个连续段。具体地，令 \(f_i = f_{i-1} \texttt{ AND } a_i\)。（需要 \(n-1\) 次操作）。再令 \(b_i = f_{i-1} \texttt{ OR } a_i\)，我们可以得到一个酷炫的只有第二种颜色第一次出现的位置变成了第三种颜色，其余位置都和 \(a\) 序列相同的序列。只要能处理这个东西，就做完了。

发现 \(\texttt{x OR y}\) 优秀的代数性质：它等于 \(-x-y\pmod 3\)。可以用它消掉相同的项，于是就做完了。具体一点，就是 \(\texttt{OR}\) 两个相同的颜色，颜色不变！！！反正就是做完了。

反正就是，操作次数 \(<6n\)，非常酷炫。

[CERC 2024] Anthem

回文串。一半的回文串。一个回文串，半个走回来，继续往前走。去重。

总结：

一、去重。
二、压缩。PAM！！！Palindrome Automaton！！！双回文串。回文串。

• 1.pre suf
  最长回文串。好困难啊。

撑台面捧哏是没问题的，但是拆台就不太好了。——aaaaaaqqqqqq

复习 Manacher！！！Manacher mAnacher maNacher manAcher manaCher manacHer manachEr manacheR。

[COCI 2022.3] Fliper

图论建模。每个挡板拆成两个点，每个点度数 \(\leq 2\)，所以图形成若干环、若干链。有若干点必须染相同颜色。

套路的想法：

把颜色相同的限制，抽象成一条边。点染色变成边染色，每个环出边颜色出现次数必须相同。虚点连自环。

四色问题 -> 0/1 染色。找出欧拉回路，间隔的边染不同颜色。染完了再染一次，变成了 0/1/2/3 染色。

[OOI 2025] Strong Connectivity Strikes Back

DAG 怎么删？删掉不影响偏序关系的所有边。

撑台面捧哏是没问题的，但是拆台就不太好了。——MYFJCHX（内心）
没关系我们看一下题解就行了。——MYFJCHX（说出来了）
无法同步更改。请检查您的网络连接。——Microsoft Whiteboard

看题解！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！！

\(k2>k1\) 咕咕嘎嘎。
否则嘎嘎咕咕。

[EC Final 2019] Permutation

笛卡尔树！不对。

它是个排列。\(1\) 左边不会跑到右边，右边不会跑到左边。好像左右两边独立的问题和原问题很像。\(f_{l,r,L,R}\) 表示 \([l,r]\) 区间的答案，并且左边 \(L\) 个可以重排，右边 \(R\) 个可以重排。直接递归。

[EC Final 2022] Binary String

操作次数感性理解很少。分成两个部分。好难啊，头有点晕。