兼职 MOer 的幸福生活（续？）

1.FFT

0.引入

以系数形式给定 \(n-1\) 次多项式 \(A\)，\(m-1\) 次多项式 \(B\)，求 \(C=A*B\)。设 \(a_i\) 为多项式 \(A\) 中 \(i\) 次项的系数，\(b_i,c_i\) 同理，则根据乘法分配律，易知 \(c_i = \sum\limits_{j=0}^i a_j b_{i-j}\)。易知 \(C\) 的次数为 \(n+m-2\)，则枚举 \(C\) 的系数暴力计算复杂度约为 \(O((n+m)^2)\)。当然，如果先枚举 \(A\) 的系数再枚举 \(B\) 的系数去计算 \(C\) 的系数，复杂度为 \(O(nm)\)。

1.正文

因为 \(C\) 是 \(n+m-2\) 次多项式，如果有其 \(n+m-1\) 个不同点值，就能确定它。设 \(N=n+m-1\)，不同点值的 \(x\) 分别为 \(x_0,x_1,\cdots,x_{N-1}\)。对于 \(x_i\)，分别代入 \(A,B\) 中计算再相乘，就能得到它对应的 \(y_i\)。如果设 \(x_i\) 代入 \(A\) 中计算的结果为 \(A_i\)，那么可将此步骤表示为：

\(\begin{bmatrix} x_0^0 &x_0^1 &x_0^2 & \cdots & x_0^{N-1} \\ x_1^0 &x_1^1 &x_1^2 & \cdots & x_1^{N-1} \\ x_2^0 &x_2^1 &x_2^2 & \cdots & x_2^{N-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{N-1}^0 & x_{N-1}^1 & x_{N-1}^2 & \cdots & x_{N-1}^{N-1} \end{bmatrix} \) \(\begin{bmatrix} a_0 \\ a_1\\ a_2\\ \vdots \\ a_{N-1}\\ \end{bmatrix} \) = \(\begin{bmatrix} A_0\\ A_1\\ A_2\\ \vdots \\ A_{N-1}\\ \end{bmatrix} \)。

经过一些聪明的发现，当 \(x_i = \omega_N^{i}\) 时，可以快速计算这个东西。

先不用管 \(\omega_N\) 是什么东西（\(N\) 次单位根），后面再写其定义与其解释。

对于当前 \(N\) 项多项式，先将其补足为离它最近的 \(2\) 的幂次。（例如 \(12\) 补成 \(16\)，\(40000\) 补成 \(65536\) 等，方便分治。）设对于当前多项式，\(f(x)=a_0x^0+a_1x^1+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7\)，考虑分治计算。设有

\(g(x)=a_0x^0+a_2x^1+a_4x^2+a_6x^3\)

\(h(x)=a_1x^0+a_3x^1+a_5x^2+a_7x^3\)（分离了奇数项和偶数项。）

则 \(f(x)=g(x^2)+x \times h(x^2)\)。

设 \(m=\frac{N}{2}\)，则 \(({\omega_N^i})^2=\omega_m^{i\%m}\)。

所以若 \(0\leq k < m\)，

\(f(\omega_N^k) = g(\omega_m^k)+\omega_N^k \times h(\omega_m^k)\)。

\(f(\omega_N^{k+m}) = g(\omega_m^k)-\omega_N^k \times h(\omega_m^k)\)。

递归计算即可。每次既要递归 \(g\) 又要递归 \(h\)，复杂度为 \(O(n\log n)\)。

现在还有两个问题：

1.单位根怎么求。
2.代码怎么写。

2.精细实现

可以发现，如果仅仅用一个数组存 \(a\)，那么递归过程中 \(a\) 被打乱了，尝试写出 \(a\) 如何被打乱。

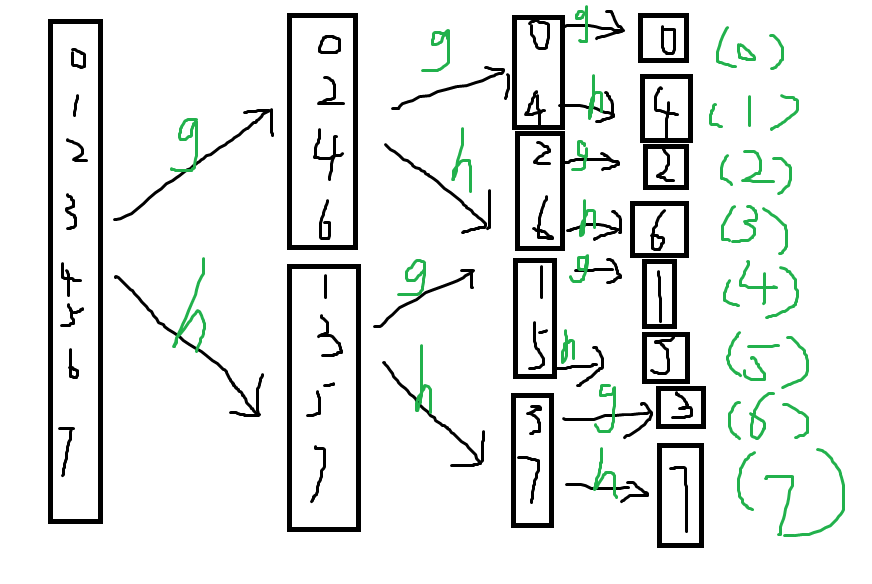
发现一个数会到其二进制反转后的那个数那里。考虑证明。 第一次分治时，分 \(g\) 还是分 \(h\) 是在为结果第一位做选择：分 \(g\) 第一位就是 \(0\)，分 \(h\) 第一位就是 \(1\)。分哪里又是根据奇偶性决定的，也就是根据原数最后一位决定的，所以结果第一位就是原数最后一位。分完过后，坐标离散化实际上就是将其右移一位，然后又变成了子问题继续划分。所以归纳得证。

于是就可以先推出最后一步的 \(a\) 数组，再从后往前还原 \(a\) 数组并计算。计算就可以直接计算了。

3.单位根相关

\(\omega_N^i = \cos(\frac{2\pi i}{n})+\sin(\frac{2\pi i}{n})\mathrm{i}\)。

4.还有一件事

通过点值还原系数。拉格朗日插值不太行，想点其它办法。
设矩阵 \(X\) = \(\begin{bmatrix} (\omega_N^0)^0 &(\omega_N^0)^1 &(\omega_N^0)^2 & \cdots & (\omega_0^0)^{N-1} \\ (\omega_N^1)^0 &(\omega_N^1)^1 &(\omega_N^1)^2 & \cdots & (\omega_N^1)^{N-1} \\ (\omega_N^2)^0 &(\omega_N^2)^1 &(\omega_N^2)^2 & \cdots & (\omega_N^2)^{N-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ (\omega_N^{N-1})^0 &(\omega_N^{N-1})^1 & (\omega_N^{N-1})^2 & \cdots & (\omega_N^{N-1})^{N-1} \end{bmatrix} \)。

根据前文，有 \(X \begin{bmatrix} c_0 \\ c_1\\ c_2\\ \vdots \\ c_{N-1}\\ \end{bmatrix} \) = \(\begin{bmatrix} C_0\\ C_1\\ C_2\\ \vdots \\ C_{N-1}\\ \end{bmatrix} \)。（\(C_i\) 的定义与 \(A_i\) 类似。）

如果能得到 \(X^{-1}\)，那么 \(\begin{bmatrix} c_0 \\ c_1\\ c_2\\ \vdots \\ c_{N-1}\\ \end{bmatrix} \) = \(X^{-1}\begin{bmatrix} C_0\\ C_1\\ C_2\\ \vdots \\ C_{N-1}\\ \end{bmatrix} \)。

事实上，\(X^{-1} = \frac{1}{N}\begin{bmatrix} (\omega_N^0)^0 &(\omega_N^0)^{-1} &(\omega_N^0)^{-2} & \cdots & (\omega_0^0)^{-(N+1)} \\ (\omega_N^1)^0 &(\omega_N^1)^{-1} &(\omega_N^1)^{-2} & \cdots & (\omega_N^1)^{-(N+1)} \\ (\omega_N^2)^0 &(\omega_N^2)^{-1} &(\omega_N^2)^{-2} & \cdots & (\omega_N^2)^{-(N+1)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ (\omega_N^{N-1})^0 &(\omega_N^{N-1})^{-1} & (\omega_N^{N-1})^{-2} & \cdots & (\omega_N^{N-1})^{-(N+1)} \end{bmatrix} \)。

直接计算即可证明 \(X^{-1}X = I\)。只要传个参就和之前一样了。（计算幂次的时候，用 \(\omega ^ {-1}\) 即可。）

Credits

我 写了这篇文章。
jr_zch 提出我写错了。
jr_zch 又提出我写错了。
我改了。
jr_zch 和 nb_jzy 提出我改错了。
jr_zch 再次提出我写错了。

2.FWT

1.Or

给定数组 \(A,B\)，设 \(C_i = \sum\limits_{j=0}^{n-1} \sum\limits_{k=0}^{n-1}A_jB_k[j|k=i]\)，求 \(C\)。这里说 \(A\) 与 \(B\) 或卷积得到 \(C\)，表示为 \(A | B = C\)。

\(O(n^2)\) 做法是显然的，但是太劣。考虑构造一个 \(FWT\) 变换，满足：

• 若 \(C = A|B\)，则 \(FWT[C] = FWT[A] * FWT[B]\)。（此处 \(*\) 为点乘。）
• 若已知 \(FWT[A]\)，可以求出唯一确定的 \(A\)。

可以发现，\(FWT[A]_i = \sum\limits_{i|j=i} A_i\) 是一个很好的 \(FWT\) 变换，即 \(FWT[A]_i\) 是 \(A\) 的 \(i\) 的子集下标之和。（式子省略了上下界。）

验证性质：

\(FWT[A]_i \times FWT[B]_i = \sum\limits_{i|j=i}\sum\limits_{i|k=i}A_jB_k\)。
\(FWT[C]_i = \sum\limits_{i|j=i} C_i\)。

发现任何满足 \(i|j=i\) 且 \(i|k=i\) 的 \(A_jB_k\) 都会被 \(C_{j|k}\) 算到贡献，因此上述两式是相等的。

可逆性待会说，先看如何求 \(FWT[A]_i\)。枚举子集。\(O(n^2)\)？\(O(3^{log_2(n)})\)？都不太优秀。

考虑迭代处理，设当前已经处理好了 \(FWT[A]_{1 \sim \frac{n}{2}}\) 和 \(FWT[A]_{\frac{n}{2}+1 \sim n}\)。需要注意的是，此处所说的处理只指的是你这段区间里的答案。相当于 \(\frac{n}{2}+1\) 还没有算 \(1\) 带来的贡献诸如此类。这是当前这一步要算的。

可以发现，\(FWT[A]_{1 \sim n}\) 就等于 \(\{FWT[A]_{1 \sim \frac{n}{2}},FWT[A]_{1 \sim \frac{n}{2}}+FWT[A]_{\frac{n}{2}+1 \sim n}\}\)。

这是因为左半部分的贡献暂时没有更新，但右半部分的贡献被左半部分更新了，因为对于 \(j+\frac{n}{2}\) 来说，它多了 \(j\) 的子集的贡献，所以要加上。

当区间长度为 \(1\) 时，\(FWT[A]_i=A_i\)。如此从小到大迭代，可以做到 \(O(n\log n)\)。

点乘后得到 \(FWT[C]\)，还原成 \(C\) 就非常简单了。同样的分析过程，同样的流程，可以得到 \(IFWT[A]_{1 \sim n} = \{IFWT[A]_{1 \sim \frac{n}{2}},IFWT[A]_{\frac{n}{2}+1 \sim n}-IFWT[A]_{1 \sim \frac{n}{2}}\}\)。可能会有些迭代顺序的疑问，但仔细分析后发现这里从小到大依然可行，而且这样变换和逆变换只需要用一个函数多传一个参就可以了。

2.And

和卷积。做法与或卷积类似。因为可以发现或运算和与运算本身就很类似。
设 \(FWT[A]_i=\sum\limits_{j|i=j} A_j\)。（即 \(i\) 为 \(j\) 的子集。）
则 \(FWT[A]_i \times FWT[B]_i = \sum\limits_{j|i=j}\sum\limits_{k|i=k}A_jB_k\)。
\(FWT[C]_i = \sum\limits_{j|i=j} C_j\)。
易得两式相等。

迭代关系也很显然，\(FWT[A]_{1 \sim n} = \{FWT[A]_{1 \sim \frac{n}{2}}+FWT[A]_{\frac{n}{2}+1 \sim n},FWT[A]_{\frac{n}{2}+1 \sim n}\}\)。
那么求逆也简单了，\(IFWT[A]_{1 \sim n} = \{IFWT[A]_{1 \sim \frac{n}{2}}-IFWT[A]_{\frac{n}{2}+1 \sim n},IFWT[A]_{\frac{n}{2}+1 \sim n}\}\)。

3.Xor

\(\{+,-\}\)，\(\{\frac{+}{2},\frac{-}{2}\}\)。

3.多项式超级无敌极端霸气究极高端神奇酷炫操作

1.多项式求逆

给定多项式 \(A\)，求 \(\frac{1}{A}\)。容易发现 \(\frac{1}{A}\) 不一定项数有限，所以一般求的是 \(\frac{1}{A} \bmod x^n\)。
设 \(\frac{1}{A}=B\)，\(B_i\) 为 \(x^i\) 的系数，易得 \(B_0 = A_0^{-1} \pmod{p}\)
假设现在已经求出了 \(B\) 的前 \(m+1\) 项的系数，现在要求 \(B_{m+1}\)。那么现在只考虑 \(x^{m+1}\) 这一项，则必须满足 \(\sum\limits_{i=0}^{m+1} A_iB_{m+1-i} = 0\)，易得 \(B_{m+1} = \frac{-\sum\limits_{i=1}^{m+1} A_iB_{m+1-i}}{A_0}\) 即 \(-B_0\sum\limits_{i=1}^{m+1} A_iB_{m+1-i}\)。直接求复杂度 \(O(n^2)\)。
下文以 \(B_i\) 表示前 \(i\) 项构成的多项式而非系数。那么考虑倍增，若当前已知 \(B_m\)，求 \(B_{2m}\)。
因为有:

\[\begin{aligned} B_{2m} \equiv B_m \pmod{x^m} \end{aligned}\]

所以：

\[\begin{aligned} B_{2m} - B_m \equiv 0 \pmod{x^m} \end{aligned}\]

两边同时平方，得到

\[\begin{aligned} {B_{2m}}^2 - 2B_{2m}B_m + {B_m}^2 \equiv 0 \pmod{x^{2m}} \end{aligned}\]

因为 \(A \times B_{2m} \equiv 1 \pmod{x^{2m}}\)，所以两边同乘 \(A\) 得

\[\begin{aligned} A{B_{2m}}^2 - 2AB_{2m}B_m + A{B_m}^2 \equiv 0 \pmod{x^{2m}} \\ B_{2m} - 2B_m + A{B_m}^2 \equiv 0 \pmod{x^{2m}} \\ B_{2m} \equiv 2B_m - A{B_m}^2 \pmod{x^{2m}} \end{aligned}\]

直接 NTT 就可以了。复杂度分析很简单，\(m\) 是 \(2^i\)，每一个 \(m\) 对应的复杂度都是 \(O(m\log m)\)，简单求和就是 \(O(n \log n)\)。

2.多项式除法

有了多项式求逆的基础，普通多项式除法就应该很简单了。所以这里主要讨论欧几里得多项式除法，即带余多项式除法。

给定次数为 \(n\) 的被除式 \(A(x)\)，次数为 \(m\) 的除式 \(B(x)\)，求商 \(D(x)\) 与余式 \(R(x)\) 满足 \(A(x) = B(x)D(x)+R(x)\)。\((m \leq n)\)。

有点难做。但是可以尝试删掉余数影响，设 \(A'(x)=A(\frac{1}{x}) \times x^n\)，\(B'(x)=B(\frac{1}{x}) \times x^m\)，\(D'(x)=D(\frac{1}{x}) \times x^{n-m}\)，\(R'(x)=R(\frac{1}{x}) \times x^{m-1}\)。可以发现其实这就是对系数做了一次 reverse。但是带来的结果很惊人。由原式可得，\(A(\frac{1}{x})=B(\frac{1}{x})D(\frac{1}{x})+R(\frac{1}{x})\)。两边同时乘以 \(x^n\)，得到 \(A(\frac{1}{x})\times x^n=B(\frac{1}{x}) \times x^m \times D(\frac{1}{x}) \times x^{n-m} + R(\frac{1}{x}) \times x^n\)。即 \(A'(x) = B'(x)D'(x)+R'(x) \times x^{n-m+1}\)。

综上，

\[\begin{aligned} A'(x)=B'(x)D'(x) \pmod{x^{n-m+1}} \end{aligned}\]

\(D'(x)\) 被完好无损地保留了下来。现在，求出 \(\frac{A'(x)}{B'(x)} \bmod x^{n-m+1}\) 就求出了所需要的 \(D'(x)\)，将其再 reverse 后就能得到 \(D(x)\) 了。这个普通多项式除法是简单的。知道 \(D(x)\) 后，\(R(x)\) 就等于 \(A(x)-B(x)D(x)\)，直接算就行了。时间复杂度 \(O(n \log n)\)。

3.常系数齐次线性递推

这个算是多项式除法（取模）的应用吧。给定 \(f_0,f_1,\dots,f_{m-1}\) 与递推式 \(f_i(i \geq m) = \sum\limits_{j=1}^m a_jf_{i-j}\)，求 \(f_n\)。
矩阵 KiraKiraDokiDoki 可以做到 \(O(m^3 \log n)\)，不讲。
写出此递推式的特征多项式为 \(x^m = \sum\limits_{i=0}^{m-1} a_{m-i}x^i\)。根据这个特征多项式，我们通过降次可以求出将 \(x^n\) 用 \(x^0 \sim x^{m-1}\) 表示的方法，这里写作 \(x^n = \sum\limits_{i=0}^{m-1}b_ix^i\)。经过一番手玩，容易发现，使用类似降次的方法，将 \(f_n\) 用 \(f_0 \sim f_{m-1}\) 表示时的系数就是 \(b\)。即 \(f_n = \sum\limits_{i=0}^{m-1} b_if_i\)。因为手玩会发现这个类似降次的流程几乎相同。倘若知道特征多项式的系数，就能通过简单地代值求出 \(f_n\)。朴素的 KiraKiraDokiDoki 是 \(O(m^2 \log n)\) 的。流程还是普通的流程，只是原本的 \(a\) 变成了一堆系数，原本的 \(ans\) 也变成了一堆系数，相乘还需要降次展开。

看起来相乘那里普通 NTT 就能优化了，但是降次展开貌似还是单次 \(O(m^2)\) 的。两个 \(m-1\) 次的多项式相乘，最高次变成了 \(2m-2\) 次。\(m \sim 2m-2\) 次项每一项都需要 \(O(m)\) 地朴素展开。

考虑这样一个事情：降次展开实际上是在对原多项式 \(\bmod (x^m - \sum\limits_{i=0}^{m-1} a_{m-i}x^i)\)。这是特征多项式移项后的版本，显然值为 \(0\)。所以，对它取模在多项式层面看来是在减去它乘另一个多项式从而让余式次数 \(<m\)，在数值层面上看来却是在不断减 \(0\)，所以得到的结果就是降次展开后的结果，值不变。

这个就可以用刚刚的多项式取模优化了，单次复杂度也变成了 \(O(m \log m)\)，总时间复杂度 \(O(m \log m \log n)\)。

4.多项式多点求值

给定次数为 \(n\) 的多项式 \(A(x)\) 和 \(m\) 个数 \(\{x_0,x_1,\dots,x_{m-1}\}\)，分别求出 \(\{A(x_0),A(x_1),\dots,A(x_{m-1})\}\)。
尝试去分治解决。将当前的点分成 \(\{x_0,x_1,\dots,x_p\}\) 和 \(\{x_{p+1},x_{p+2},\dots,x_{m-1}\}\) 两部分。构造多项式 \(f_0 = \prod\limits_{i=0}^{p}(x-x_i)\)，\(f_1 = \prod\limits_{i=p+1}^{m-1}(x-x_i)\)。然后算出 \(A_0 = A \bmod f_0\)，\(A_1 = A \bmod f_1\)，再把第一部分点分给 \(A_0\)，第二部分点分给 \(A_1\)，得到两个规模减小的原问题。为什么它是对的呢？以第一部分为例，当 \(f_0\) 取第一部分的任何点值时，其值都为 \(0\)。因此，\(A \bmod f_0\) 在多项式层面看来是在减去 \(f_0\) 乘另一个多项式从而得到 \(A_0\)，在数值层面上看来却是在不断减 \(0\)，值不变。所以它是对的。
复杂度分析也不难，第一层先将 \(A\) 对 \(\prod\limits_{i=0}^{m-1}(x-x_i)\) 取模，降次，取模是 \(O(n \log n)\) 的，算这个除式用简单分治能做到 \(O(m \log^2 m)\)。接下来的第 \(i\) 层，每层的长度 \(m'\) 近似看作 \(\frac{m}{2^i}\)，\(f\) 是可以通过前文简单分治预处理的，只考虑取模的话复杂度就是 \(O(\frac{m}{2^i} \log m)\)，一层总共 \(2^i\) 个取模，所以单层复杂度 \(O(m \log m)\)。总时间复杂度为 \(O(m \log^2 m+n \log n)\)。

5.多项式开方

给定一个 \(n-1\) 次的多项式 \(A\)，求多项式 \(B\) 满足 \(B^2 \equiv A \pmod{x^n}\)
有暴力做法，不写了。
考虑倍增，若当前求出 \(B_m\)，想要求 \(B_{2m}\)。
步骤同 1.多项式求逆，能得到式子：

\[\begin{aligned} {B_{2m}}^2 - 2B_{2m}B_m + {B_m}^2 \equiv 0 \pmod{x^{2m}} \end{aligned}\]

因为 \({B_{2m}}^2 \equiv A \pmod{x^{2m}}\)，所以有

\[\begin{aligned} A - 2B_{2m}B_m + {B_m}^2 \equiv 0 \pmod{x^{2m}} \end{aligned}\]

整理可得

\[\begin{aligned} B_{2m} \equiv \frac{A+{B_m}^2}{2B_m} \pmod{x^{2m}} \end{aligned}\]

直接求即可，同 1.多项式求逆 分析可得，总时间复杂度为 \(O(n\log n)\)。

6.多项式求导/积分

我不会。乱写一通。

首先，若 \(f(x)=x^n\)，则 \(f'(x) = nx^{n-1}\)，这是普通幂函数的求导，是显然的。然后又因为若 \(h(x)=f(x)+g(x)\)，则 \(h'(x)=f'(x)+g'(x)\)，所以能推出多项式 \(F(x)=\sum\limits_{i=0}^n a_i x^i\) 的导函数 \(F'(x)\) 为 \(\sum\limits_{i=0}^{n-1}a_{i+1}(i+1)x^i\)。

多项式求导显然能做到 \(O(n)\)。

积分与求导互为逆运算，所以把 \(F(x)\) 积一下就变成了 \(\sum\limits_{i=0}^n \frac{a_i}{i+1} x^{i+1}\)。

多项式积分显然也能做到 \(O(n)\)。

7.多项式 \(\ln\)/\(\exp\)

我不会。乱写一通。

先将 \(\ln(f(x))\) 求导。

\[\begin{aligned} \ln(f(x))' &= \frac{d\ln}{df(x)}f'(x) \\ &= \frac{1}{f(x)} f'(x) \\ &= \frac{f'(x)}{f(x)} \end{aligned}\]

求导后的函数相当好求，只需要多项式求逆和多项式求导还有多项式乘法即可。然后再把它积回去，就能得到原函数 \(\ln(f(x))\) 了。需要注意的是，积分时不知道常数项，但是这不重要，常数项必定为 \(0\)。设 \(\ln(f(x))\) 常数项为 \(a_0\)，则 \(f(x)\) 常数项因为 \(e^{a_0}\)，看起来只有 \(a_0=0\) 时这玩意在模意义下有意义，实际上我也认为只有 \(a_0=0\) 时这玩意在模意义下有意义。也就是说当且仅当 \(f(x)\) 的常数项为 \(1\) 时，可以算出 \(\ln(f(x))\)。

然后是多项式 \(\exp\)。

在这之前，需要先提一嘴 Newton's Method，在这里即多项式牛顿迭代（牛顿也干了）。

在这之前，需要先提一嘴泰勒展开（泰勒也干了）。

泰勒展开指的是，如果 \(f\) 具有无穷阶可导性，那么有

\[\begin{aligned} f(x)=\sum\limits_{i=0}^{+\infty}\frac{f^{(i)}(a)}{i!}(x-a)^i \end{aligned}\]

然后多项式牛顿迭代，解决的是这样一类问题：找到一个关于 \(x\) 的多项式 \(f(x)\)，满足对于一个关于 \(f(x)\) 的多项式 \(g(f(x))\)，\(g(f(x)) \equiv 0 \pmod{x^n}\) 成立。再考虑多项式 \(h(x)\)，它与我们想解决的问题有关，若想求逆元，就有 \(g(f(x))=h(x)-f^{-1}(x)\)；若想求根号，就有 \(g(f(x)) = h(x)-f^2(x)\)。这里就有一件需要注意的事情了，虽然说知道的是 \(g(f(x))\)，但看这些式子的话会发现知道的实际是 \(h(x)\)，通过 \(h(x)\) 等于 \(f(x)\) 的某种变换来求出 \(h(x)\) 的某种变换。

可能还是有点抽象，举个例子，假设现在想求 \(\sqrt{h(x)}\)，就构造 \(g(f(x))=h(x)-f^2(x)\)，又因为 \(g(f(x)) \equiv 0 \pmod{x^n}\)，所以 \(h(x) \equiv f^2(x) \pmod{x^n}\)，即最终求出的 \(f(x)\) 才是我们想要的 \(\sqrt{h(x)}\)。

下面来说做法。依然考虑倍增，先找到 \(g(f(x)) \equiv 0 \pmod{x^1}\) 的 \(f(x)\)。这个东西应该是没有通解的，只能根据具体的 \(g(f(x))\) 去构造。

设当前已经求出了 \(f_m\)，现在想求 \(f_{2m}\)（与前几条目用过的记号类似。）

将 \(g(f_{2m}(x))\) 在 \(f_m(x)\) 处泰勒展开，得到

\[\begin{aligned} g(f_{2m}(x)) \equiv \sum\limits_{i=0}^{+\infty}\frac{g^{(i)}(f_m(x))}{i!}(f_{2m}(x)-f_m(x))^i \equiv 0 \pmod{x^{2m}} \end{aligned}\]

此时，发现只用保留前两项即可。为什么？若 \(f_{2m}(x) \equiv f_m(x) \pmod{x^{2m}}\)，则后面 \(i\) 次方那一项始终为 \(0\)，这样的话保留多少项都一样了。否则，\(f_{2m}(x)\) 与 \(f_m(x)\) 的前 \(m\) 项必定相等，则其差的最小有效项次数至少为 \(m\)。因此，但凡其指数 \(\geq 2\)，该求和项最小有效项次数至少为 \(2m\)，\(\bmod x^{2m}\) 后就没了。

所以有

\[\begin{aligned} g(f_{2m}(x)) = g(f_m(x)) + g'(f_m(x))(f_{2m}(x)-f_m(x)) \pmod{x^{2m}} \end{aligned}\]

移项整理得

\[\begin{aligned} f_{2m}(x) \equiv f_m(x) - \frac{g(f_m(x))}{g'(f_m(x))} \pmod{x^{2m}} \end{aligned}\]

注意到 \(g(f_m(x))\) 与 \(g'(f_m(x))\) 都是可以用已知量表示的，那么理论上就做完了，复杂度 \(O(n \log n)\)。

现在就是真正求 \(\exp\) 的时候了。

构造 \(g(f(x)) = h(x) - \ln f(x)\)，\(f(x)\) 即为所求。

每次迭代的时候，\(g(f_m(x)) = h(x) - \ln f_m(x)\)，而其导数可以看作与 \(h\) 无关，那么显然 \(g'(f_m(x)) = -\frac{1}{f_m(x)}\)。代入迭代即可。

求多项式 \(\ln\) 与多项式 \(\exp\) 复杂度均为 \(O(n \log n)\)。

参考博客：
https://www.cnblogs.com/T-Y-P-E/p/10211909.html
https://www.cnblogs.com/feiko/p/newtons_method.html

写得都很好。

8.多项式KiraKiraDokiDoki

现在给定多项式 \(B(x)\)，要求多项式 \(A(x) \equiv B^k(x) \pmod{x^n}\)。由题意，\(\ln A(x) \equiv k \ln B(x) \pmod{x^n}\)。需要注意的是，这里的 \(k\) 要取模的话应该是对 \(p\) 取模，而不是 \(φ(p)\)，这是因为这里的目的是让多项式变成 \(e\) 的若干次方，也就是说 \(\ln\) 才是指数，而求 \(\ln\) 就很显然是对 \(p\) 取模了，不能搞混淆。

由 \(\ln B(x)\) 可以求出 \(\ln A(x)\)，再 \(\exp\) 回去就是答案。即 \(A(x) \equiv \exp(k \ln B(x)) \pmod{x^n}\)。但是这是 \(b_0 = 1\) 时的答案。如果 \(b_0 \neq 1\)，就不能对它直接求 \(\ln\)。所以，设 \(B\) 的最低次数有效项是 \(b_ix^i\)，则

\[\begin{aligned} A(x) &\equiv B^k(x)\\ &\equiv (b_ix^i \times \frac{B(x)}{b_ix^i})^k\\ &\equiv {b_i}^kx^{ik} \exp(k \ln \frac{B(x)}{b_ix^i}) \pmod{x^n} \end{aligned}\]

当然，如果 \(ik\) 太大，那么直接输出全 \(0\) 多项式就行了。时间复杂度显然为 \(O(n\log n)\)。