费用流(直接应用)
1.概念
所有最大可行流中费用的最小/最大值
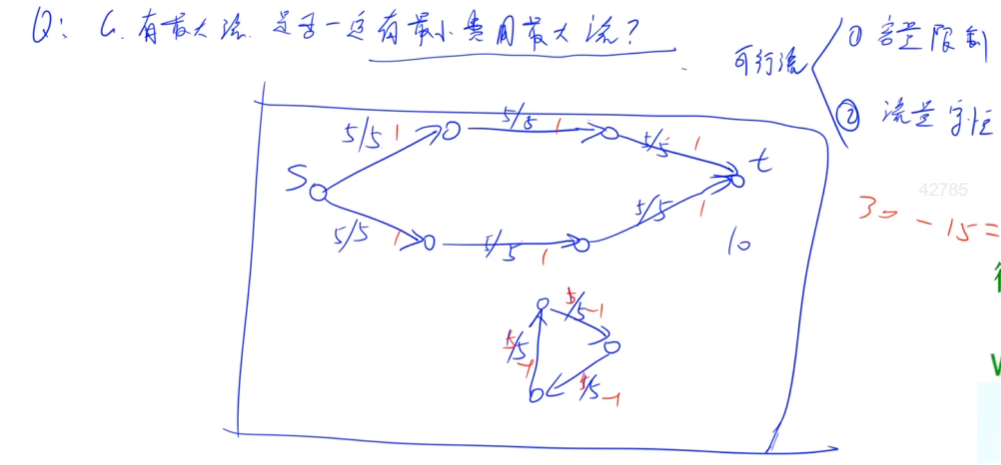
上图中的最小费用最大流就是15
每条边都有一个权值w,这条边如果流量是c,那么这条边的费用就是c*w
2.求法
把EK算法中的bfs函数换成spfa求源点到汇点的一条最短路即可
模板(普通)
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=200010,M=1000010,INF=1e15;//根据边的大小,来调整N,M,INF
typedef pair<int,int> PII;
int n, m, S, T;
int h[N], e[M], f[M], w[M], ne[M], idx;
int q[N], d[N], pre[N], incf[N];
bool st[N];
void add(int a, int b, int c, int d)
{
e[idx] = b, f[idx] = c, w[idx] = d, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, w[idx] = -d, ne[idx] = h[b], h[b] = idx ++ ;
}
bool spfa()
{
int hh = 0, tt = 1;
memset(d, 0x3f, sizeof d);
memset(incf, 0, sizeof incf);
q[0] = S, d[S] = 0, incf[S] = INF;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int ver = e[i];
if (f[i] && d[ver] > d[t] + w[i])
{
d[ver] = d[t] + w[i];
pre[ver] = i;
incf[ver] = min(f[i], incf[t]);
if (!st[ver]){
q[tt++]=ver;
if (tt==N) tt=0;
st[ver]=true;
}
}
}
}
return incf[T]>0;
}
void EK(int& flow, int& cost){
flow=cost=0;
while(spfa()){
int t=incf[T];
flow+=t,cost+=t*d[T];
for (int i=T;i!=S;i=e[pre[i] ^ 1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
}
void slove(){
cin>>n>>m>>S>>T;
memset(h,-1,sizeof h);
while(m--){
int a,b,c,d;
cin>>a>>b>>c>>d;
add(a,b,c,d);
}
int flow,cost;
EK(flow,cost);
cout<<flow<<" "<<cost<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}
dijkstra势能优化+spfa(快一倍)
// Author: YE Minghan
#include<bits/stdc++.h>
using namespace std;
#ifdef DEBUG
#include "templates/debug.h"
#else
#define dbg(...) (void)0
#define here (void)0
#endif
using ll=long long;
using VI=vector<int>;
using PII=pair<int,int>;
#define endl '\n'
#define PB emplace_back
#define PPB pop_back
#define MP make_pair
#define ALL(Name) Name.begin(),Name.end()
#define GI greater<int>
#define fi first
#define se second
struct MCMF
{
private:
static const ll INF=4e18;
int n,m,S,T;
struct E
{
int v;
ll cap,cost;
int rev;
};
vector<vector<E>> g;
vector<ll> dis,h;
vector<PII> pre;
void spfa()
{
queue<int>q;
fill(h.begin()+1,h.end(),0);
h[S]=0,q.push(S);
while(!q.empty())
{
int x=q.front();q.pop();
for(int i=0;i<g[x].size();i++)
{
auto [y,f,c,r]=g[x][i];
if(f&&h[y]>h[x]+c)h[y]=h[x]+c,q.push(y);
}
}
}
void dijk()
{
priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<> >q;
fill(dis.begin()+1,dis.end(),INF);
dis[S]=0,q.emplace(0,S);
while(!q.empty())
{
auto [d,x]=q.top();q.pop();
if(dis[x]!=d)continue;
for(int i=0;i<g[x].size();i++)
{
auto [y,f,c,r]=g[x][i];
if(f&&dis[y]>dis[x]+c+h[x]-h[y])pre[y]={x,i},q.emplace(dis[y]=dis[x]+c+h[x]-h[y],y);
}
}
}
public:
MCMF(){}
MCMF(int node,int sink,int terminal)
{
n=node,S=sink,T=terminal;
g=vector<vector<E>>(node+1);
dis=h=vector<ll>(node+1);
pre=vector<PII>(node+1);
}
void add(int u,int v,ll cap,ll cost)
{
g[u].PB(E{v,cap, cost,(int)g[v].size() });
g[v].PB(E{u,0 ,-cost,(int)g[u].size()-1});
}
pair<ll,ll> Flow(ll flow=INF)
{
ll totflow=0,totcost=0;
spfa();
while(totflow<flow)
{
dijk();
if(dis[T]>=INF/2)break;
ll co=0,fl=flow-totflow;
for(int i=T;i!=S;)
{
auto [u,id]=pre[i];
auto [v,f,c,r]=g[u][id];
co+=c,fl=min(fl,f);
i=u;
}
totflow+=fl,totcost+=fl*co;
for(int i=T;i!=S;)
{
auto [u,id]=pre[i];
auto &[v,f,c,r]=g[u][id];
f-=fl,g[v][r].cap+=fl;
i=u;
}
for(int i=1;i<=n;i++)h[i]+=dis[i];
}
return {totflow,totcost};
}
};
int main()
{
ios::sync_with_stdio(false),cin.tie(nullptr);
// int _;cin>>_;while(_--)
int n,m,S,T;
cin>>n>>m>>S>>T;
MCMF f(n,S,T);
for(int i=1,u,v,w,c;i<=m;i++)
cin>>u>>v>>w>>c,f.add(u,v,w,c);
auto [fl,co]=f.Flow();
cout<<fl<<" "<<co<<endl;
return 0;
}
运输问题

#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=200010,M=1000010,INF=1e15;//根据边的大小,来调整N,M,INF
typedef pair<int,int> PII;
int n, m, S, T;
int h[N], e[M], f[M], w[M], ne[M], idx;
int q[N], d[N], pre[N], incf[N];
bool st[N];
void add(int a, int b, int c, int d)
{
e[idx] = b, f[idx] = c, w[idx] = d, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, w[idx] = -d, ne[idx] = h[b], h[b] = idx ++ ;
}
bool spfa()
{
int hh = 0, tt = 1;
memset(d, 0x3f, sizeof d);
memset(incf, 0, sizeof incf);
q[0] = S, d[S] = 0, incf[S] = INF;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int ver = e[i];
if (f[i] && d[ver] > d[t] + w[i])
{
d[ver] = d[t] + w[i];
pre[ver] = i;
incf[ver] = min(f[i], incf[t]);
if (!st[ver]){
q[tt++]=ver;
if (tt==N) tt=0;
st[ver]=true;
}
}
}
}
return incf[T]>0;
}
void EK(int& flow, int& cost){
flow=cost=0;
while(spfa()){
int t=incf[T];
flow+=t,cost+=t*d[T];
for (int i=T;i!=S;i=e[pre[i] ^ 1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
}
void slove(){
cin>>m>>n;
S=0,T=m+n+1;
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++){
int x;cin>>x;
add(S,i,x,0);
}
for(int i=1;i<=n;i++){
int x;cin>>x;
add(m+i,T,x,0);
}
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++){
int x;cin>>x;
add(i,m+j,INF,x);
}
int flow,cost;
EK(flow,cost);
cout<<cost<<endl;
for(int i=0;i<idx;i+=2){
f[i]+=f[i^1],f[i^1]=0;
w[i]=-w[i],w[i^1]=-w[i^1];
}
EK(flow,cost);
cout<<-cost<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}

#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=200010,M=1000010,INF=1e15;//根据边的大小,来调整N,M,INF
typedef pair<int,int> PII;
int n, m, S, T;
int h[N], e[M], f[M], w[M], ne[M], idx;
int q[N], d[N], pre[N], incf[N];
bool st[N];
int s[N];
void add(int a, int b, int c, int d)
{
e[idx] = b, f[idx] = c, w[idx] = d, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, w[idx] = -d, ne[idx] = h[b], h[b] = idx ++ ;
}
bool spfa()
{
int hh = 0, tt = 1;
memset(d, 0x3f, sizeof d);
memset(incf, 0, sizeof incf);
q[0] = S, d[S] = 0, incf[S] = INF;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int ver = e[i];
if (f[i] && d[ver] > d[t] + w[i])
{
d[ver] = d[t] + w[i];
pre[ver] = i;
incf[ver] = min(f[i], incf[t]);
if (!st[ver]){
q[tt++]=ver;
if (tt==N) tt=0;
st[ver]=true;
}
}
}
}
return incf[T]>0;
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=t*d[T];
for (int i=T;i!=S;i=e[pre[i] ^ 1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
void slove(){
cin>>n;
S=0,T=n+1;
memset(h,-1,sizeof h);
int tot=0;
for(int i=1;i<=n;i++){
cin>>s[i];
//先对相邻的两点之间连边
tot+=s[i];
add(i,i<n?i+1:1,INF,1);
add(i,i>1?i-1:n,INF,1);
}
tot/=n;
for(int i=1;i<=n;i++){
if(tot<s[i]) add(S,i,s[i]-tot,0);//高于平均值的,需要流出s[i]-tot的货物
else if(tot>s[i]) add(i,T,tot-s[i],0);//低于的需要被入tot-s[i]的货物
}
cout<<EK()<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=200010,M=1000010,INF=1e15;//根据边的大小,来调整N,M,INF
typedef pair<int,int> PII;
int n, m, S, T;
int h[N], e[M], f[M], w[M], ne[M], idx;
int q[N], d[N], pre[N], incf[N];
bool st[N];
void add(int a, int b, int c, int d)
{
e[idx] = b, f[idx] = c, w[idx] = d, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, w[idx] = -d, ne[idx] = h[b], h[b] = idx ++ ;
}
bool spfa()
{
int hh = 0, tt = 1;
memset(d, 0x3f, sizeof d);
memset(incf, 0, sizeof incf);
q[0] = S, d[S] = 0, incf[S] = INF;
while (hh != tt)
{
int t = q[hh ++ ];
if (hh == N) hh = 0;
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int ver = e[i];
if (f[i] && d[ver] > d[t] + w[i])
{
d[ver] = d[t] + w[i];
pre[ver] = i;
incf[ver] = min(f[i], incf[t]);
if (!st[ver]){
q[tt++]=ver;
if (tt==N) tt=0;
st[ver]=true;
}
}
}
}
return incf[T]>0;
}
int EK(){
int cost=0;
while(spfa()){
int t=incf[T];
cost+=t*d[T];
for (int i=T;i!=S;i=e[pre[i] ^ 1]){
f[pre[i]]-=t;
f[pre[i]^1]+=t;
}
}
return cost;
}
void slove(){
cin>>n;
memset(h,-1,sizeof h);
S=0,T=2*n+1;
for(int i=1;i<=n;i++){
add(S,i,1,0);
add(n+i,T,1,0);
}
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
int x;
cin>>x;
add(i,n+j,1,x);
}
cout<<EK()<<endl;
for(int i=0;i<idx;i+=2){
f[i]+=f[i^1],f[i^1]=0;
w[i]=-w[i],w[i^1]=-w[i^1];
}
cout<<-EK()<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}

规则一:直接拆点即可,出点与入点之间的容量为1,点与点之间的边的容量也为1
规则二:点与点之间的边的容量设为1即可
规则三:不限制容量
int main()
{
int cnt = 0;
scanf("%d%d", &m, &n);
S = ++ cnt;
T = ++ cnt;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m + i - 1; j ++ )
{
scanf("%d", &cost[i][j]);
id[i][j] = ++ cnt;
}
// 规则1
memset(h, -1, sizeof h), idx = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m + i - 1; j ++ )
{
//id[i][j]*2表示入点,id[i][j]*2+1表示出点
add(id[i][j] * 2, id[i][j] * 2 + 1, 1, cost[i][j]);//该点的入点向出点连边
if (i == 1) add(S, id[i][j] * 2, 1, 0);//源点向起点的入点连边
if (i == n) add(id[i][j] * 2 + 1, T, 1, 0);//终点的出点向汇点连边
if (i < n)
{
add(id[i][j] * 2 + 1, id[i + 1][j] * 2, 1, 0);
add(id[i][j] * 2 + 1, id[i + 1][j + 1] * 2, 1, 0);
}
}
printf("%d\n", EK());
// 规则2
memset(h, -1, sizeof h), idx = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m + i - 1; j ++ )
{
add(id[i][j] * 2, id[i][j] * 2 + 1, INF, cost[i][j]);
if (i == 1) add(S, id[i][j] * 2, 1, 0);
if (i == n) add(id[i][j] * 2 + 1, T, INF, 0);
if (i < n)
{
add(id[i][j] * 2 + 1, id[i + 1][j] * 2, 1, 0);
add(id[i][j] * 2 + 1, id[i + 1][j + 1] * 2, 1, 0);
}
}
printf("%d\n", EK());
// 规则3
memset(h, -1, sizeof h), idx = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m + i - 1; j ++ )
{
add(id[i][j] * 2, id[i][j] * 2 + 1, INF, cost[i][j]);
if (i == 1) add(S, id[i][j] * 2, 1, 0);
if (i == n) add(id[i][j] * 2 + 1, T, INF, 0);
if (i < n)
{
add(id[i][j] * 2 + 1, id[i + 1][j] * 2, INF, 0);
add(id[i][j] * 2 + 1, id[i + 1][j + 1] * 2, INF, 0);
}
}
printf("%d\n", EK());
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号