最大流判定+拆点
1.最短路径转最大流

trick:无向图的话,就是建立反边,并且容量均为设定的f[i]即可
思路就是:二分答案x,然后对于权值大于x的容量都设为0,小于等于x的话f[i]设为1,源点是1,汇点是n,如果最大流的值>=K,那么x可以作为答案
代码:
#include<bits/stdc++.h>
#define x first
#define y second
#define endl '\n'
#define int long long
using namespace std;
const int N=2e5,M=2e5,INF=1e15;//根据边的大小,来调整N,M,INF
int n,m,S,T,K;
int h[N],e[M],f[M],ne[M],idx,w[M];//l数组记录的是每条边的下界
int q[N],d[N],cur[N];//A[i]表示所有进入i这个点的边的流量下界之和-所有从i点出去的边的流量下界之和
void add(int a,int b,int c){
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
e[idx]=a,w[idx]=c,ne[idx]=h[b],h[b]=idx++;
}
bool bfs(){//规划分层图,然后判断是否存在增广路
int hh=0,tt=0;
memset(d,-1,sizeof d);
q[0]=S,d[S]=0,cur[S]=h[S];//起点的层数为0
while(hh<=tt){
int t=q[hh++];
for(int i=h[t];~i;i=ne[i]){
int ver=e[i];
if(d[ver]==-1&&f[i]){//只有这条边有流量的时候,才能继续走下去
d[ver]=d[t]+1;
cur[ver]=h[ver];
if(ver==T)return true;//如果能搜到T的话,那么就说明可以找到一条增广路
q[++tt]=ver;
}
}
}
return false;
}
int find(int u,int limit){
if(u==T) return limit;
int flow=0;
for(int i=cur[u];~i&&flow<limit;i=ne[i]){//当前弧优化
cur[u]=i;
int ver=e[i];
if(d[ver]==d[u]+1&&f[i]){
int t=find(ver,min(f[i],limit-flow));
if(!t) d[ver]= -1;
f[i]-=t,f[i^1]+=t,flow+=t;
}
}
return flow;
}
int dinic(){
int ans=0,flow;
while(bfs()) while(flow=find(S,INF)) ans+=flow;
return ans;
}
bool check(int x){
for(int i=0;i<idx;i++){
if(w[i]<=x) f[i]=1;
else f[i]=0;
}
if(dinic()>=K) return true;
return false;
}
void slove(){
cin>>n>>m>>K;
memset(h,-1,sizeof h);
for(int i=1;i<=m;i++){
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
S=1,T=n;
int l=1,r=1e6;
while(l<r){
int mid=(l+r)/2;
if(check(mid)) r=mid;
else l=mid+1;
}
cout<<l<<endl;
}
signed main(){
ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
int T=1;
while(T--) slove();
}
2.星际转移问题
https://www.luogu.com.cn/problem/P2754
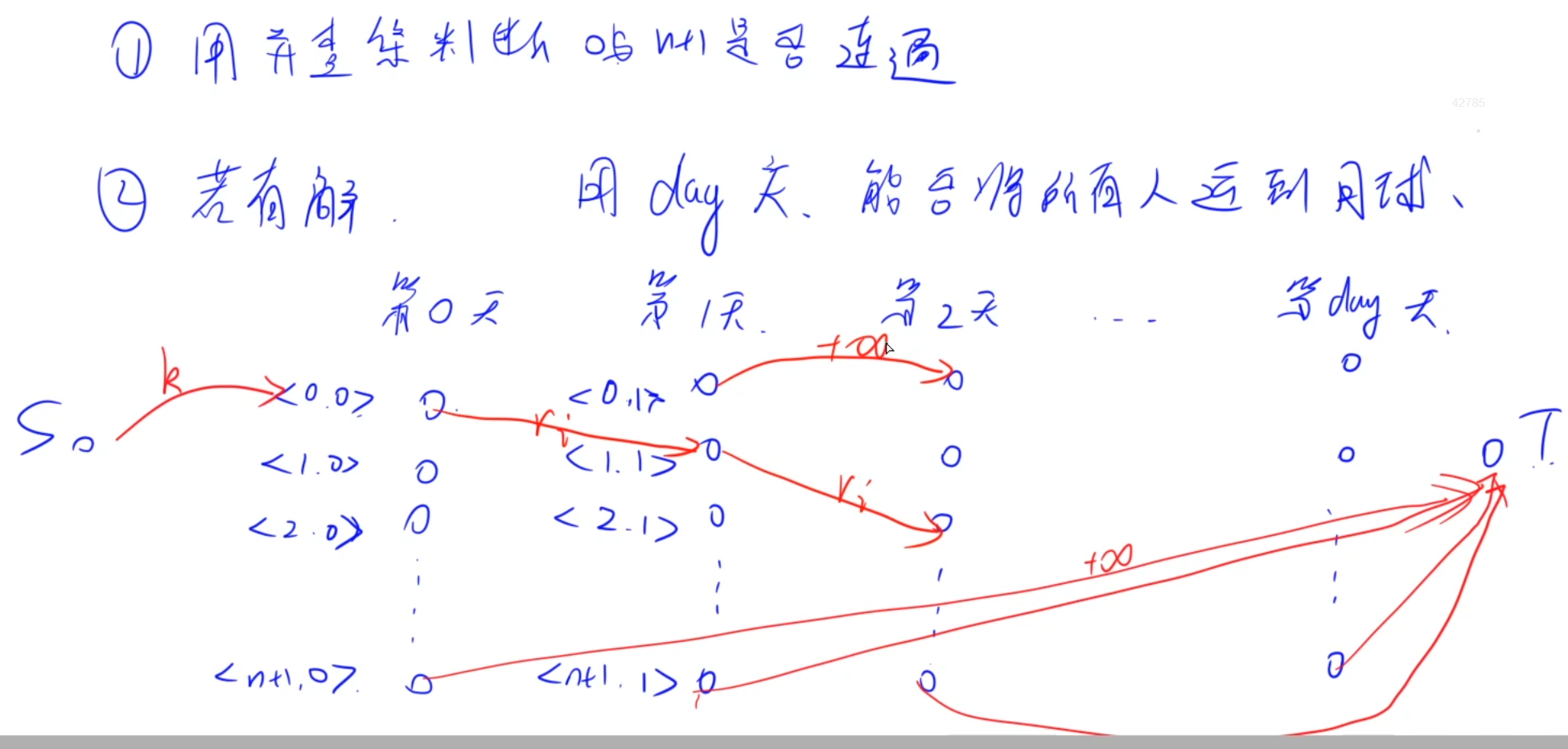
枚举答案,而不是二分答案,因为从小到大枚举答案,图的框架是只会做增加而不会做减法,所以枚举到下一个天数答案的时候就是在原有的残留网络上新加一些点和边即可
首先源点连向第0天的第0个公交站,容量为k,然后就是第i天的第i个公交站连向他下一天能到达的站,容量为ri,然后第i天的第i个公交站连向第i+1天的第i个公交站,容量为正无穷,表示留在这个站一整天,不移动。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1101 * 50 + 10, M = (N + 1100 + 20 * 1101) + 10, INF = 1e8;
int n, m, k, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];
struct Ship{
int h, r, id[30];
}ships[30];
int p[30];
int find(int x){
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
int get(int i, int day){//<点,天数>是一个点,这个是返回编号
return day * (n + 2) + i;
}
void add(int a, int b, int c){
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx ++ ;
}
bool bfs(){
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
q[0] = S, d[S] = 0, cur[S] = h[S];
while (hh <= tt){
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i]){
int ver = e[i];
if (d[ver] == -1 && f[i]){
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if (ver == T) return true;
q[ ++ tt] = ver;
}
}
}
return false;
}
int find(int u, int limit){
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]){
cur[u] = i;
int ver = e[i];
if (d[ver] == d[u] + 1 && f[i]){
int t = find(ver, min(f[i], limit - flow));
if (!t) d[ver] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic(){
int r = 0, flow;
while (bfs()) while (flow = find(S, INF)) r += flow;
return r;
}
int main(){
scanf("%d%d%d", &n, &m, &k);
S = N - 2, T = N - 1;
memset(h, -1, sizeof h);
for (int i = 0; i < 30; i ++ ) p[i] = i;
for (int i = 0; i < m; i ++ ){
int a, b;
scanf("%d%d", &a, &b);
ships[i] = {a, b};
for (int j = 0; j < b; j ++ ){//读入所有太空站的编号
int id;
scanf("%d", &id);
if (id == -1) id = n + 1;
ships[i].id[j] = id;
if (j){//合并一下并查集
int x = ships[i].id[j - 1];
p[find(x)] = find(id);
}
}
}
if (find(0) != find(n + 1)) puts("0");//如果不连通的话,那么就无解
else{
add(S, get(0, 0), k);//源点向最开始的起点连一条容量为k的边,表示人数
add(get(n + 1, 0), T, INF);//到达月球的话,就能到达T
int day = 1, res = 0;
while (true){
add(get(n + 1, day), T, INF);//月球向汇点连一条边
for (int i = 0; i <= n + 1; i ++ )
add(get(i, day - 1), get(i, day), INF);//横向变,表示这一站的人停留在该站一天
for (int i = 0; i < m; i ++ ){//m个公交车遍历加边
int r = ships[i].r;
int a = ships[i].id[(day - 1) % r], b = ships[i].id[day % r];
add(get(a, day - 1), get(b, day), ships[i].h);
}
res += dinic();//进行一次增广
if (res >= k) break;
day ++ ;
}
printf("%d\n", day);
}
return 0;
}
最大流之拆点--餐饮

首先是想当然的建图,但这样的建图会导致一头牛可以吃多分餐食,这也会导致答案变大,所以问题的关键在于如何控制牛的数量?
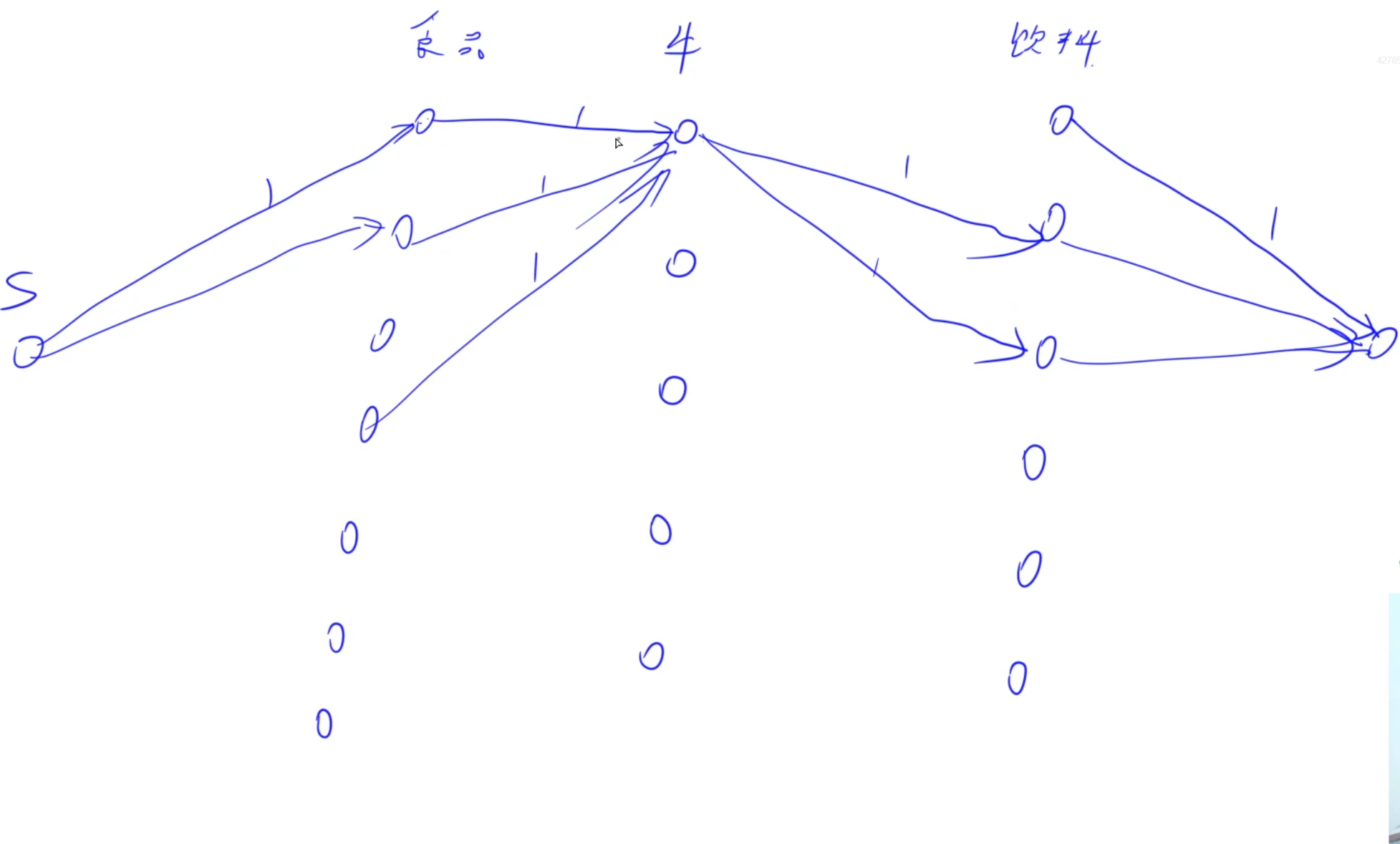
最大流常见的技巧拆点,把一个点拆为入点和出点,在这里我们可以把牛拆成一个入点和一个出点,并且连向容量为1的边,这样的话,一个牛最多只能吃一份餐食
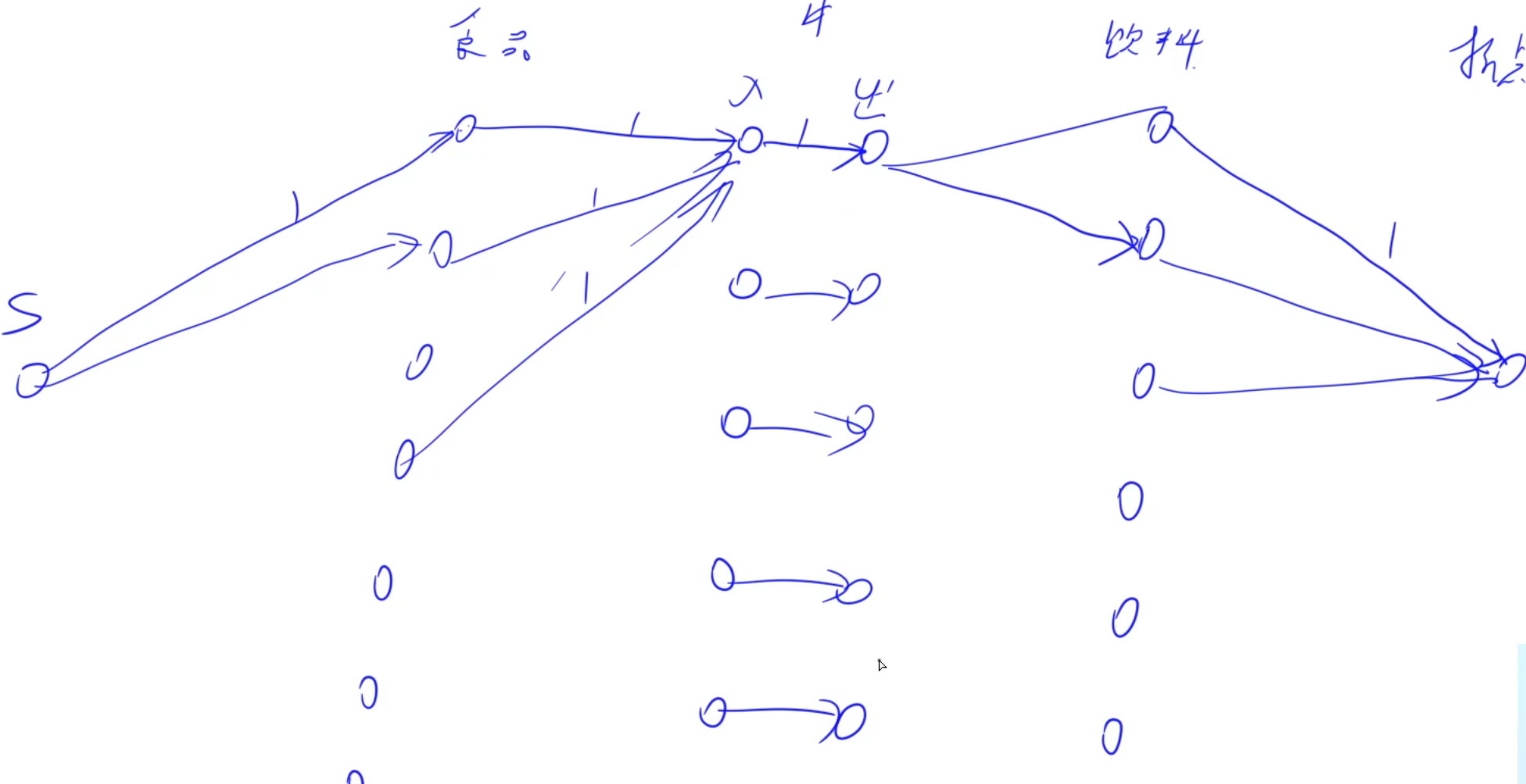
总结:当对边有限制的时候,直接对边的容量进行限定即可,对点有限制的时候,可以把一个点拆成入点和出点,并且入点和出点之间的连边容量即为限制
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 410, M = 40610, INF = 1e8;
int n, F, D, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];
void add(int a, int b, int c){
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx ++ ;
}
bool bfs(){
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
q[0] = S, d[S] = 0, cur[S] = h[S];
while (hh <= tt){
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i]){
int ver = e[i];
if (d[ver] == -1 && f[i]){
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if (ver == T) return true;
q[ ++ tt] = ver;
}
}
}
return false;
}
int find(int u, int limit){
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]){
cur[u] = i;
int ver = e[i];
if (d[ver] == d[u] + 1 && f[i]){
int t = find(ver, min(f[i], limit - flow));
if (!t) d[ver] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic(){
int r = 0, flow;
while (bfs()) while (flow = find(S, INF)) r += flow;
return r;
}
int main(){
scanf("%d%d%d", &n, &F, &D);
S = 0, T = n * 2 + F + D + 1;
memset(h, -1, sizeof h);
for (int i = 1; i <= F; i ++ ) add(S, n * 2 + i, 1);
for (int i = 1; i <= D; i ++ ) add(n * 2 + F + i, T, 1);
for (int i = 1; i <= n; i ++ ){
add(i, n + i, 1);
int a, b, t;
scanf("%d%d", &a, &b);
while (a -- ){
scanf("%d", &t);
add(n * 2 + t, i, 1);
}
while (b -- ){
scanf("%d", &t);
add(i + n, n * 2 + F + t, 1);
}
}
printf("%d\n", dinic());
return 0;
}
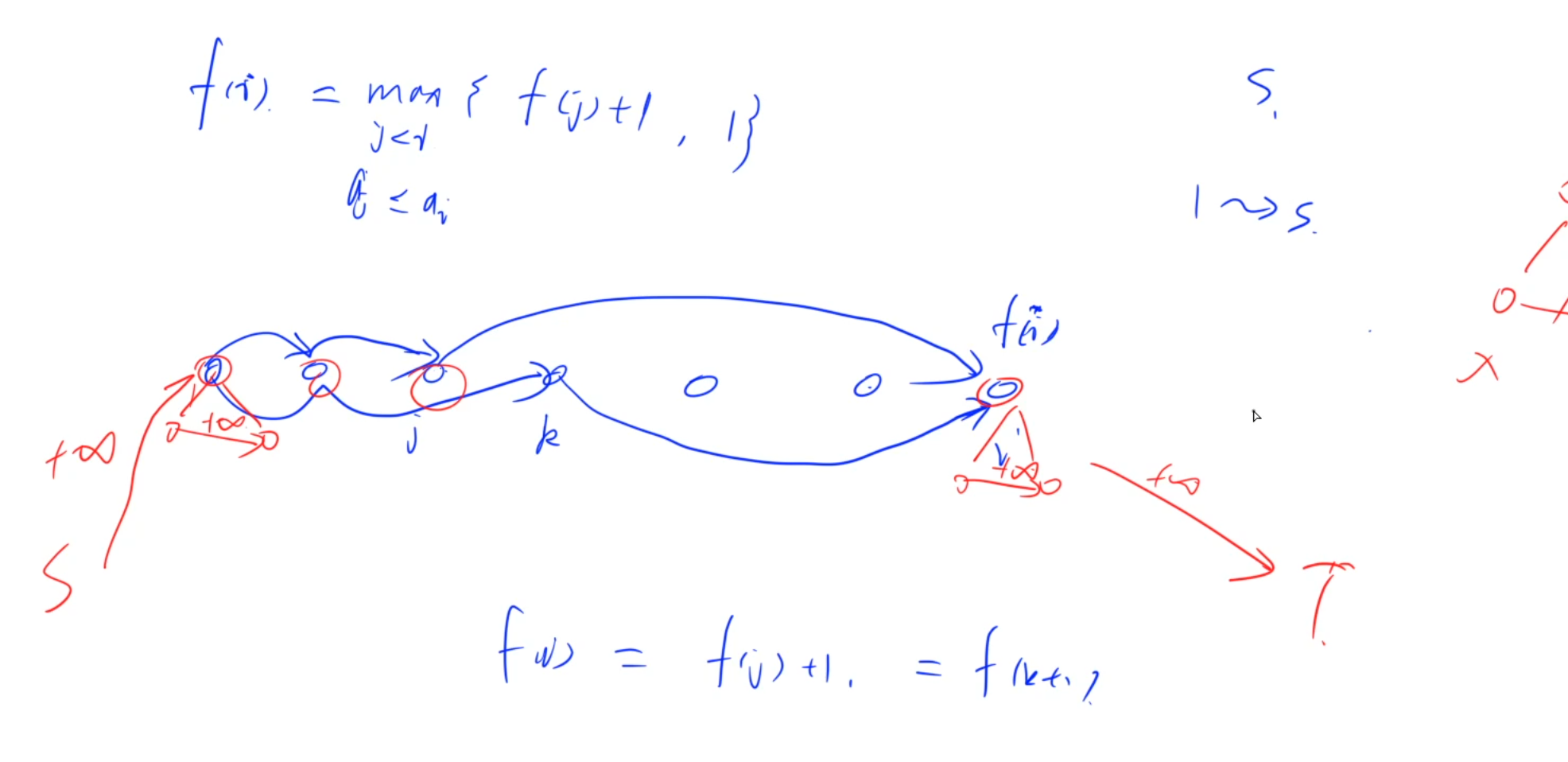
拆点--最长上升子序列问题

第一问:
简单dp,直接写即可
第二问:
只有满足f[i]=f[j]+1并且a[j]<=a[i]的时候,才能存在j->i的一条边
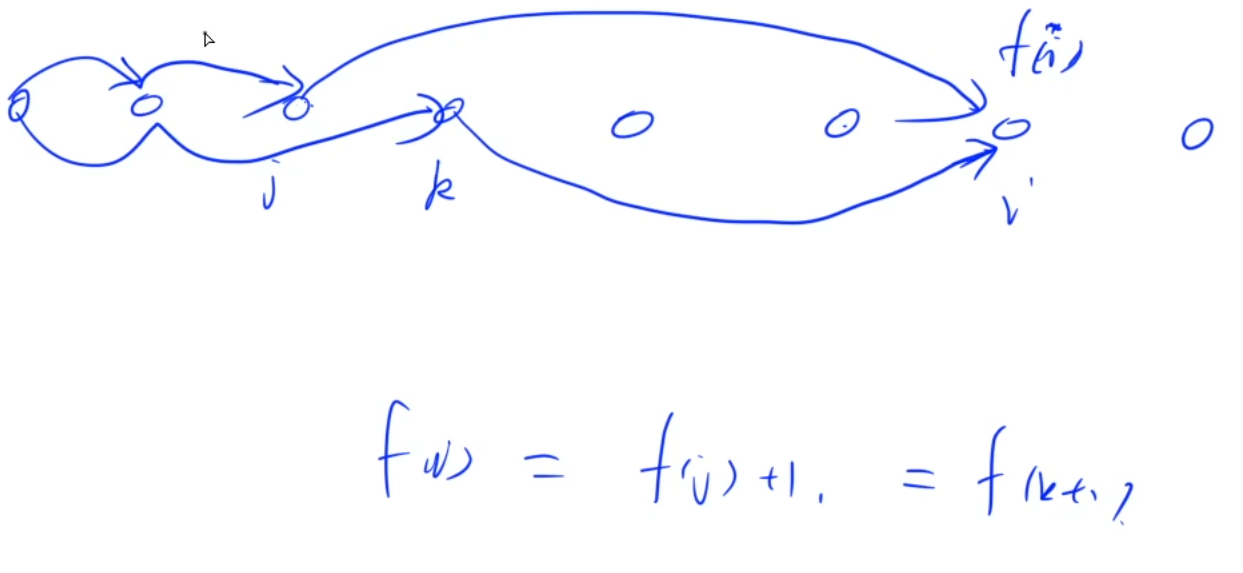
要解决第二问:
首先每个点只能选一次,所以对每个点都要进行拆点,然后源点对于所有f[i]=1的点连边,所有f[i]=s的点对于汇点连边
第三问:
第一个点的入点指向出点的容量设为正无穷,源点向第一个的容量设为正无穷
对于最后一个点也是同理,入点指向出点正无穷,如果f[n]=s,则指向汇点的容量设为正无穷
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1010, M = 251010, INF = 1e8;
int n, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];
int g[N], w[N];
void add(int a, int b, int c){
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx ++ ;
}
bool bfs(){
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
q[0] = S, d[S] = 0, cur[S] = h[S];
while (hh <= tt){
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i]){
int ver = e[i];
if (d[ver] == -1 && f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if (ver == T) return true;
q[ ++ tt] = ver;
}
}
}
return false;
}
int find(int u, int limit){
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]){
cur[u] = i;
int ver = e[i];
if (d[ver] == d[u] + 1 && f[i]){
int t = find(ver, min(f[i], limit - flow));
if (!t) d[ver] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic(){
int r = 0, flow;
while (bfs()) while (flow = find(S, INF)) r += flow;
return r;
}
int main(){
scanf("%d", &n);
S = 0, T = n * 2 + 1;
memset(h, -1, sizeof h);
for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
int s = 0;
for (int i = 1; i <= n; i ++ ){
add(i, i + n, 1);//入点向出点连边
g[i] = 1;
for (int j = 1; j < i; j ++ ) //dp更新
if (w[j] <= w[i])
g[i] = max(g[i], g[j] + 1);
for (int j = 1; j < i; j ++ )//连边
if (w[j] <= w[i] && g[j] + 1 == g[i])
add(n + j, i, 1);//第j个点的出点向第i个点的入点连边
s = max(s, g[i]);
if (g[i] == 1) add(S, i, 1);//1~n表示入点,n+1~2n表示出点,这个表示源点向这个点连边
}
for (int i = 1; i <= n; i ++ )
if (g[i] == s)
add(n + i, T, 1);//向汇点连边
printf("%d\n", s);
if (s == 1) printf("%d\n%d\n", n, n);//特判一下
else{
int res = dinic();
printf("%d\n", res);
for (int i = 0; i < idx; i += 2){//更新一下第三问的边的容量
int a = e[i ^ 1], b = e[i];
if (a == S && b == 1) f[i] = INF;
else if (a == 1 && b == n + 1) f[i] = INF;
else if (a == n && b == n + n) f[i] = INF;
else if (a == n + n && b == T) f[i] = INF;
}
printf("%d\n", res + dinic());
}
return 0;
}
拆点--企鹅
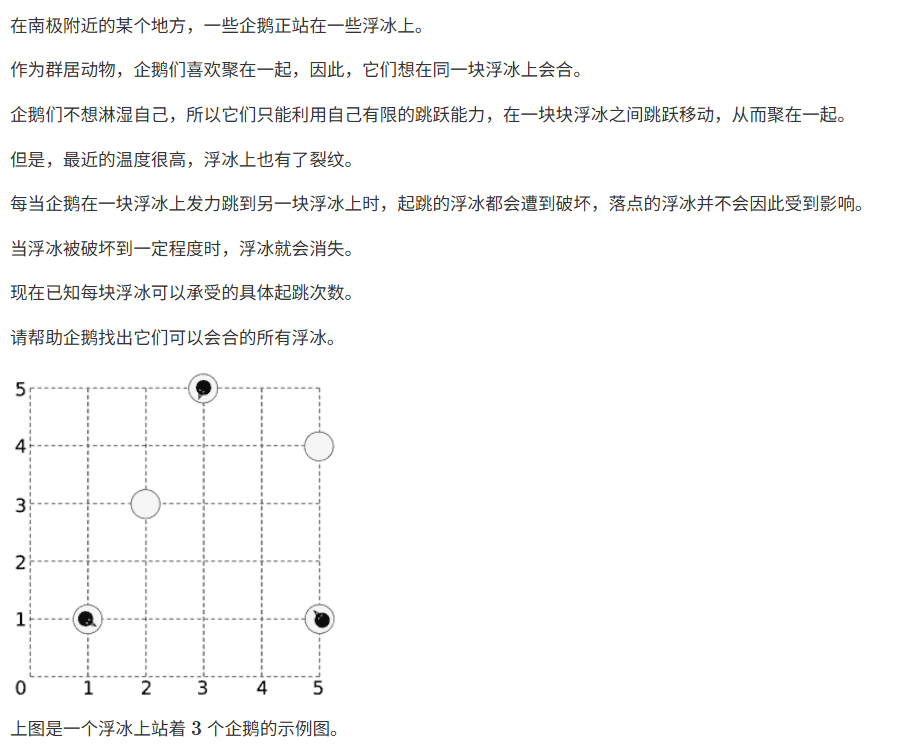
1.首先枚举汇点,判断答案是否能是这个汇点
2.源点向每个冰块连边,边容量为起始的冰块上企鹅的数量
3.拆点,对于每个冰块拆成入点和出点,容量为起跳的数量的限制
#include <iostream>
#include <cstring>
#include <algorithm>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 210, M = 20410, INF = 1e8;
const double eps = 1e-8;
int n, S, T;
double D;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];
PII p[N];
bool check(PII a, PII b){
double dx = a.x - b.x, dy = a.y - b.y;
return dx * dx + dy * dy < D * D + eps;
}
void add(int a, int b, int c){
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx ++ ;
}
bool bfs(){
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
q[0] = S, d[S] = 0, cur[S] = h[S];
while (hh <= tt){
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i]){
int ver = e[i];
if (d[ver] == -1 && f[i]){
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if (ver == T) return true;
q[ ++ tt] = ver;
}
}
}
return false;
}
int find(int u, int limit){
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]){
cur[u] = i;
int ver = e[i];
if (d[ver] == d[u] + 1 && f[i]){
int t = find(ver, min(f[i], limit - flow));
if (!t) d[ver] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic(){
int r = 0, flow;
while (bfs()) while (flow = find(S, INF)) r += flow;
return r;
}
int main(){
int cases;
scanf("%d", &cases);
while (cases -- ){
memset(h, -1, sizeof h);
idx = 0;
scanf("%d%lf", &n, &D);
S = 0;
int tot = 0;
for (int i = 1; i <= n; i ++ ){
int x, y, a, b;
scanf("%d%d%d%d", &x, &y, &a, &b);
p[i] = {x, y};
add(S, i, a);//冰块上的企鹅数量
add(i, n + i, b);//冰块的承载能力
tot += a;
}
for (int i = 1; i <= n; i ++ )
for (int j = i + 1; j <= n; j ++ )
if (check(p[i], p[j])){
add(n + i, j, INF);
add(n + j, i, INF);
}
int cnt = 0;
for (int i = 1; i <= n; i ++ ){//枚举汇点
T = i;
for (int j = 0; j < idx; j += 2){//把残留网络重新加回到容量
f[j] += f[j ^ 1];
f[j ^ 1] = 0;
}
if (dinic() == tot){
printf("%d ", i - 1);
cnt ++ ;
}
}
if (!cnt) puts("-1");
else puts("");
}
return 0;
}
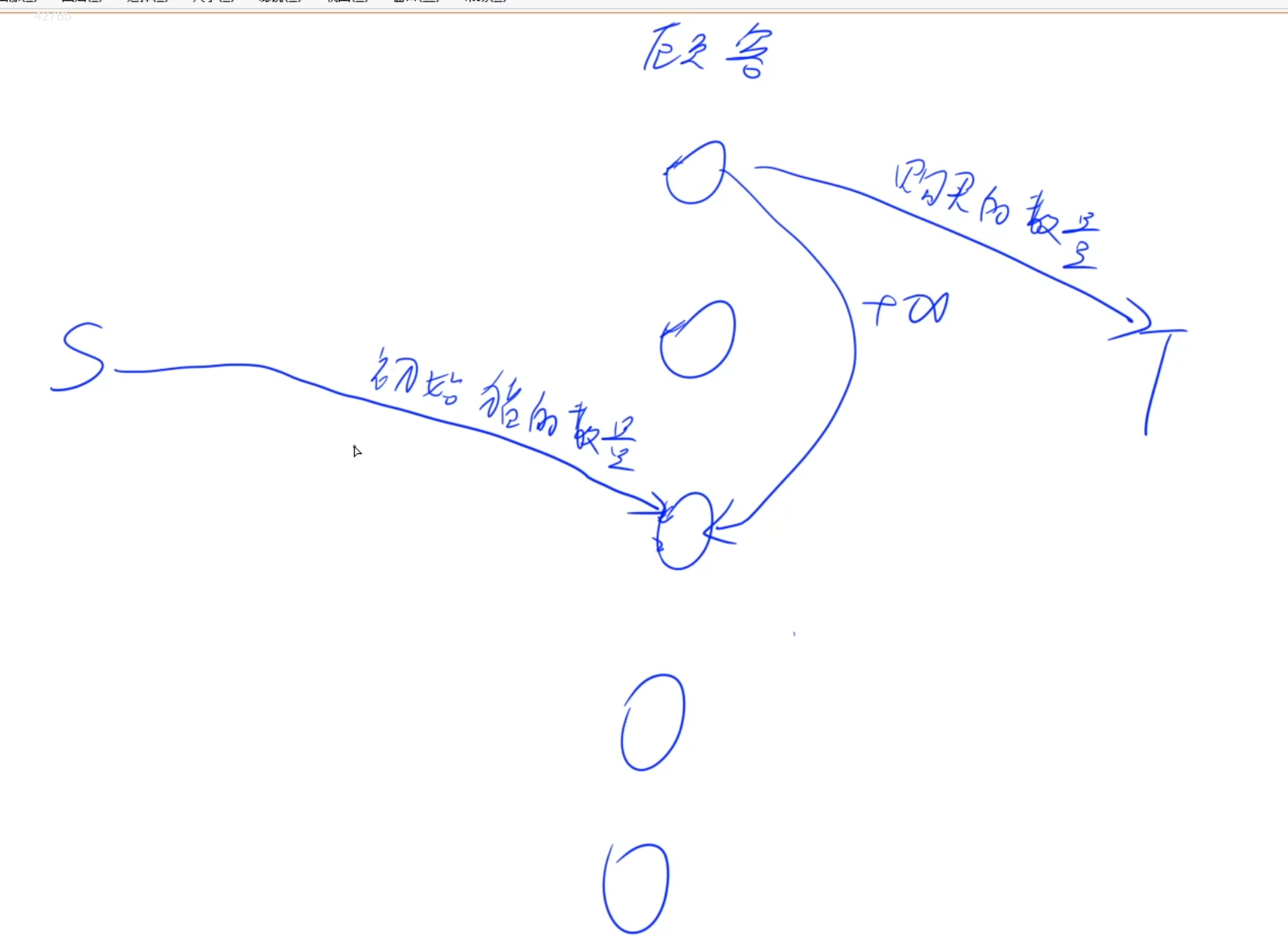
猪

很巧妙的建图
1.按照顺序从源点分配给依次前来的顾客
2.如果说一个猪舍是第一次被这个顾客访问到的话,那么就从源点接一条边到这个顾客,容量是这个猪舍的起始猪的数目
3.如果这个猪舍不是被这个顾客第一次访问的话,那么就由上一个访问过这个猪舍的顾客向本次访问这个猪舍的顾客连向一条容量为正无穷的边,因为这个猪舍是被上一个顾客接受的,并且由上一个顾客任意支配,所以
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110, M = 100200 * 2 + 10, INF = 1e8;
int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];
int w[1010], belong[1010];
void add(int a, int b, int c){
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx ++ ;
}
bool bfs(){
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
q[0] = S, d[S] = 0, cur[S] = h[S];
while (hh <= tt){
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i]){
int ver = e[i];
if (d[ver] == -1 && f[i]){
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if (ver == T) return true;
q[ ++ tt] = ver;
}
}
}
return false;
}
int find(int u, int limit){
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]){
cur[u] = i;
int ver = e[i];
if (d[ver] == d[u] + 1 && f[i]){
int t = find(ver, min(f[i], limit - flow));
if (!t) d[ver] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic(){
int r = 0, flow;
while (bfs()){
r += find(S, INF);
flow = find(S, INF);
if (flow) puts("!");
r += flow;
}
return r;
}
int main(){
scanf("%d%d", &m, &n);
S = 0, T = n + 1;
memset(h, -1, sizeof h);
for (int i = 1; i <= m; i ++ ) scanf("%d", &w[i]);//猪舍的数目
for (int i = 1; i <= n; i ++ ){//n个人的信息
int a, b;
scanf("%d", &a);
while (a -- ){
int t;
scanf("%d", &t);
if (!belong[t]) add(S, i, w[t]);//如果这个猪是第一次被这个顾客访问的话
else add(belong[t], i, INF);//上次访问的这个顾客向当前这个人连边
belong[t] = i;
}
scanf("%d", &b);
add(i, T, b);
}
printf("%d\n", dinic());
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号