笛卡尔树

概念

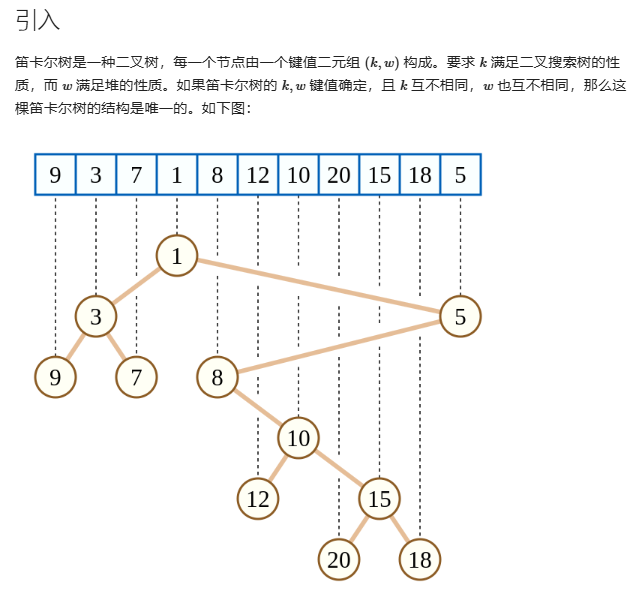
一个区间的最小值作为根节点,然后左子树就是最小值左边区间的点,右子树是最小值右边区间的点,然后也是同理,左子树的根是左边区间的最小值,右子树一致

性质

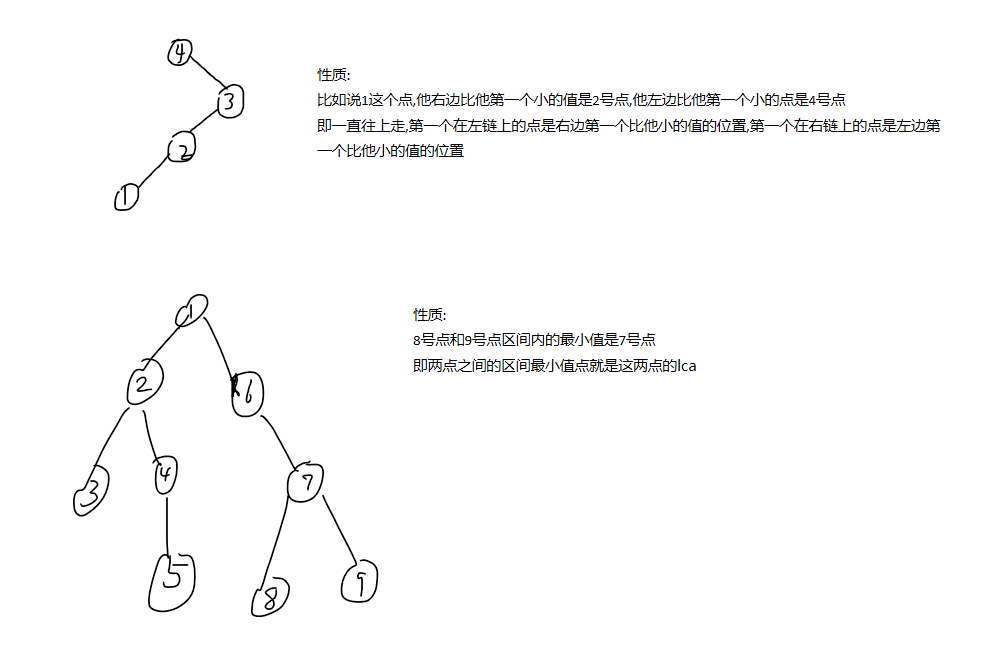
板子:

int a[N],l[N],r[N],root,n;

void build(){
	//单调栈维护右链 
	stack<int> st;
	for(int i=1;i<=n;i++){
		int last=0;
		while(!st.empty()&&a[st.top()]>a[i]){
			last=st.top();
			st.pop();
		}
		if(!st.empty()) r[st.top()]=i;
		else root=i;
		l[i]=last;
		st.push(i); 
	}	
} 

例题:

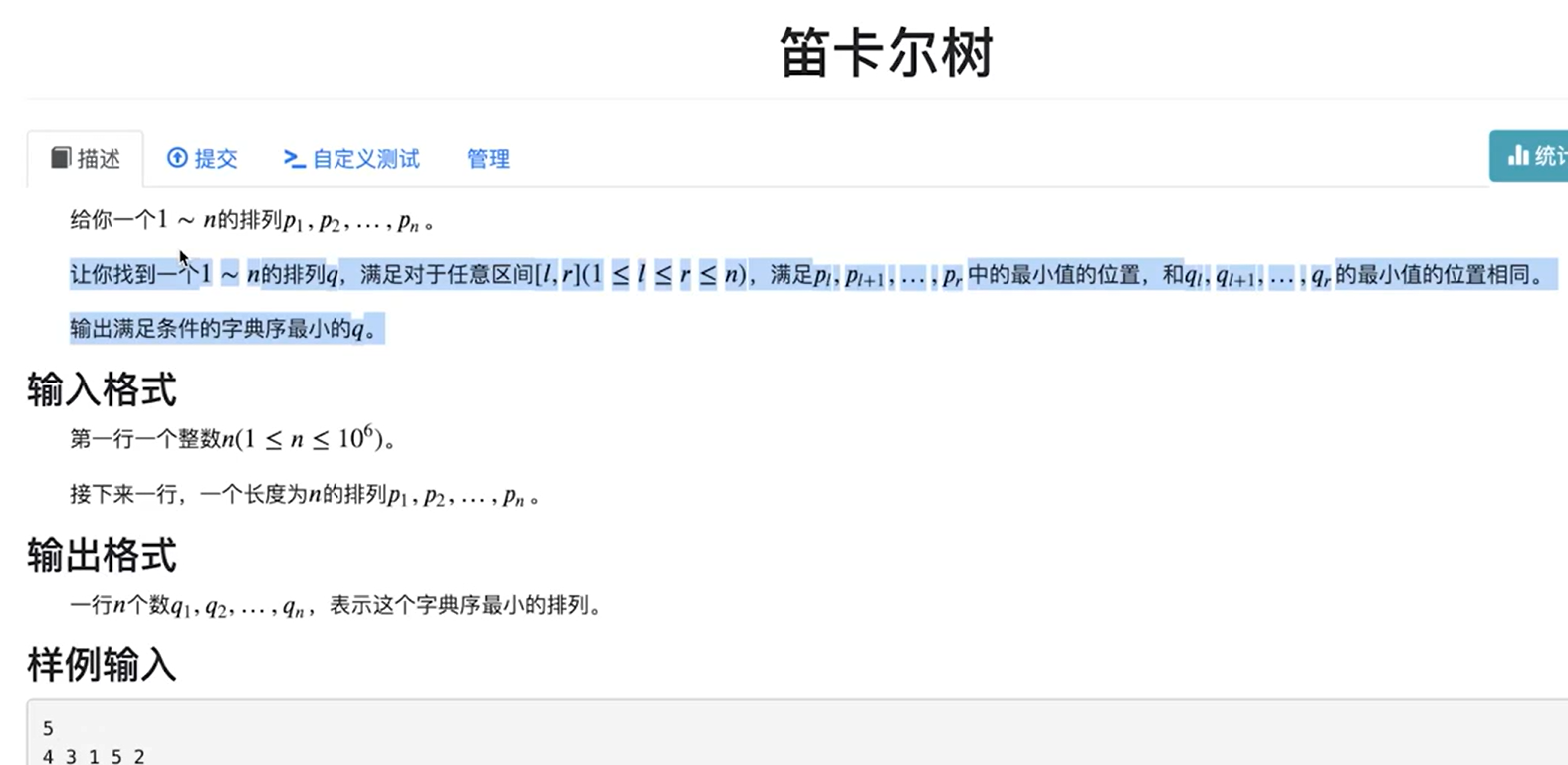
首先可以发现一个性质就是,如果对于任意区间来说,两个排列的最小值位置是一样的,那么就可以说明这两个排列的笛卡尔树的形态应当是一致的
然后贪心填值,到最后,字典序一定是最小的

#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define x first
#define y second
#define int long long 
const int N=1e6+5,mod=998244353;

int a[N],l[N],r[N],root,n,ans[N],tot;

void dfs(int u){
	ans[u]=++tot;
	if(l[u])dfs(l[u]);
	if(r[u])dfs(r[u]);
}

void build(){
	//单调栈维护右链 
	stack<int> st;
	for(int i=1;i<=n;i++){
		int last=0;
		while(!st.empty()&&a[st.top()]>a[i]){
			last=st.top();
			st.pop();
		}
		if(!st.empty()) r[st.top()]=i;
		else root=i;
		l[i]=last;
		st.push(i); 
	}	
	dfs(root); 
}

void slove(){
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	build();
	for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
	cout<<endl;
}

signed main(){
	ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
	int T=1;
	while(T--) slove();
}