最大流之上下界可行流

一.无汇源上下界可行流

有关网络流的一些自我感觉比较通透的理解?以本题为例

若一个图是满流的,此时源点指向一个点,并且容量是W,那么就说明这个点要帮助源点向外输出W的流量,若汇点指向一个点,并且容量是W,那么就说明这个点要向汇点多输出W的流量,即接收别的点W的流量

#include<bits/stdc++.h>

#define x first
#define y second
#define endl '\n'
#define int long long
 
using namespace std;

const int N=10010,M=200010,INF=1e15;//根据边的大小,来调整N,M,INF

int n,m,S,T;
int h[N],e[M],f[M],l[M],ne[M],idx;//l数组记录的是每条边的下界
int q[N],d[N],cur[N],A[N];//A[i]表示所有进入i这个点的边的流量下界之和-所有从i点出去的边的流量下界之和

void add(int a,int b,int c,int d){
	e[idx]=b,f[idx]=d-c,l[idx]=c,ne[idx]=h[a],h[a]=idx++;
	e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}

bool bfs(){//规划分层图,然后判断是否存在增广路
	int hh=0,tt=0;
	memset(d,-1,sizeof d);
	q[0]=S,d[S]=0,cur[S]=h[S];//起点的层数为0
	while(hh<=tt){
		int t=q[hh++];
		for(int i=h[t];~i;i=ne[i]){
			int ver=e[i];
			if(d[ver]==-1&&f[i]){//只有这条边有流量的时候,才能继续走下去
				d[ver]=d[t]+1;
				cur[ver]=h[ver];
				if(ver==T)return true;//如果能搜到T的话,那么就说明可以找到一条增广路
				q[++tt]=ver;
			}
		}
	}
	return false;
}

int find(int u,int limit){
	if(u==T) return limit;
	int flow=0;
	for(int i=cur[u];~i&&flow<limit;i=ne[i]){//当前弧优化
		 cur[u]=i;
		 int ver=e[i];
		 if(d[ver]==d[u]+1&&f[i]){
		 	int t=find(ver,min(f[i],limit-flow));
		 	if(!t) d[ver]=-1;
		 	f[i]-=t,f[i^1]+=t,flow+=t;
		 }
	}
	return flow;
}

int dinic(){
	int ans=0,flow;
	while(bfs()) while(flow=find(S,INF)) ans+=flow;
	return ans;
}

void slove(){
	memset(h,-1,sizeof h);
	cin>>n>>m;
	S=0,T=n+1;
	for(int i=0;i<m;i++){
		int a,b,c,d;
		cin>>a>>b>>c>>d;
		add(a,b,c,d);
		A[a]-=c,A[b]+=c;
	}
	
	//建图
	int tot=0;
	for(int i=1;i<=n;i++){
		if(A[i]>0) add(S,i,0,A[i]),tot+=A[i];
		else if(A[i]<0) add(i,T,0,-A[i]);
	}
	
	if(dinic()!=tot)cout<<"NO"<<endl;
	else{
		cout<<"YES"<<endl;
		for(int i=0;i<m*2;i+=2){//枚举正向边的流量使用情况
			cout<<f[i^1]+l[i]<<endl;//当前边的流量就是反向边t的f[t];
		}
	}     
}

signed main(){
	ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
	int T=1;
	while(T--) slove();
}

二.有汇源上下界最大流

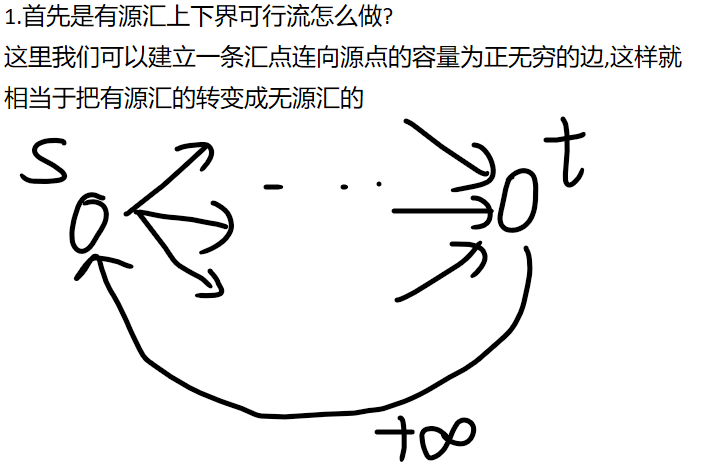
做法:

首先把有源汇上下界可行流转化为无源汇上下界可行流,即t->s连一条边,求完之后的话我们可以求一下虚拟源点和虚拟汇点之间的最大流,如果是满流的话,我们在当前的残留网络上删掉t->s,删完之后求一下s->t的最大流
求完之后,我们求出来的最大可行流+原有的流量(t->s)就是最终答案

#include<bits/stdc++.h>

#define x first
#define y second
#define endl '\n'
#define int long long
 
using namespace std;

const int N=210,M=(210+10000)*2,INF=1e15;//根据边的大小,来调整N,M,INF

int n,m,S,T;
int h[N],e[M],f[M],ne[M],idx;//l数组记录的是每条边的下界
int q[N],d[N],cur[N],A[N];//A[i]表示所有进入i这个点的边的流量下界之和-所有从i点出去的边的流量下界之和

void add(int a,int b,int c){
	e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
	e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; 
}

bool bfs(){//规划分层图,然后判断是否存在增广路
	int hh=0,tt=0;
	memset(d,-1,sizeof d);
	q[0]=S,d[S]=0,cur[S]=h[S];//起点的层数为0
	while(hh<=tt){
		int t=q[hh++];
		for(int i=h[t];~i;i=ne[i]){
			int ver=e[i];
			if(d[ver]==-1&&f[i]){//只有这条边有流量的时候,才能继续走下去
				d[ver]=d[t]+1;
				cur[ver]=h[ver];
				if(ver==T)return true;//如果能搜到T的话,那么就说明可以找到一条增广路
				q[++tt]=ver;
			}
		}
	}
	return false;
}

int find(int u,int limit){
	if(u==T) return limit;
	int flow=0;
	for(int i=cur[u];~i&&flow<limit;i=ne[i]){//当前弧优化
		 cur[u]=i;
		 int ver=e[i];
		 if(d[ver]==d[u]+1&&f[i]){
		 	int t=find(ver,min(f[i],limit-flow));
		 	if(!t) d[ver]= -1;
		 	f[i]-=t,f[i^1]+=t,flow+=t;
		 }
	}
	return flow;
}

int dinic(){
	int ans=0,flow;
	while(bfs()) while(flow=find(S,INF)) ans+=flow;
	return ans;
}

void slove(){
	memset(h,-1,sizeof h);
	int s,t;
	cin>>n>>m>>s>>t;
	S=0,T=n+1;
	for(int i=0;i<m;i++){
		int a,b,c,d;
		cin>>a>>b>>c>>d;
		add(a,b,d-c);
		A[a]-=c,A[b]+=c;
	}
	
	int tot=0;
	for(int i=1;i<=n;i++){
		if(A[i]>0) add(S,i,A[i]),tot+=A[i];
		else if(A[i]<0) add(i,T,-A[i]);
	}

	add(t,s,INF);

	if(dinic()<tot)cout<<"No Solution"<<endl;
	else {
		int res=f[idx-1];//首先看t->s的边的容量
		S=s,T=t;
		f[idx-1]=f[idx-2]=0;//删去t->s的边的容量
		cout<<res+dinic()<<endl; 
	}
}

signed main(){
	ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
	int T=1;
	while(T--) slove();
}

三.有汇源上下界最小流

s->t的流量最大等价于从t->s的流量最小,如果说想要s->t的值最小的话,那么就是求t->s的最大流

#include<bits/stdc++.h>

#define x first
#define y second
#define endl '\n'
#define int long long
 
using namespace std;

const int N=50010,M=(N+1250010)*2,INF=1e15;//根据边的大小,来调整N,M,INF

int n,m,S,T;
int h[N],e[M],f[M],ne[M],idx;//l数组记录的是每条边的下界
int q[N],d[N],cur[N],A[N];//A[i]表示所有进入i这个点的边的流量下界之和-所有从i点出去的边的流量下界之和

void add(int a,int b,int c){
	e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
	e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++; 
}

bool bfs(){//规划分层图,然后判断是否存在增广路
	int hh=0,tt=0;
	memset(d,-1,sizeof d);
	q[0]=S,d[S]=0,cur[S]=h[S];//起点的层数为0
	while(hh<=tt){
		int t=q[hh++];
		for(int i=h[t];~i;i=ne[i]){
			int ver=e[i];
			if(d[ver]==-1&&f[i]){//只有这条边有流量的时候,才能继续走下去
				d[ver]=d[t]+1;
				cur[ver]=h[ver];
				if(ver==T)return true;//如果能搜到T的话,那么就说明可以找到一条增广路
				q[++tt]=ver;
			}
		}
	}
	return false;
}

int find(int u,int limit){
	if(u==T) return limit;
	int flow=0;
	for(int i=cur[u];~i&&flow<limit;i=ne[i]){//当前弧优化
		 cur[u]=i;
		 int ver=e[i];
		 if(d[ver]==d[u]+1&&f[i]){
		 	int t=find(ver,min(f[i],limit-flow));
		 	if(!t) d[ver]= -1;
		 	f[i]-=t,f[i^1]+=t,flow+=t;
		 }
	}
	return flow;
}

int dinic(){
	int ans=0,flow;
	while(bfs()) while(flow=find(S,INF)) ans+=flow;
	return ans;
}

void slove(){
	memset(h,-1,sizeof h);
	int s,t;
	cin>>n>>m>>s>>t;
	S=0,T=n+1;
	for(int i=0;i<m;i++){
		int a,b,c,d;
		cin>>a>>b>>c>>d;
		add(a,b,d-c);
		A[a]-=c,A[b]+=c;
	}
	
	int tot=0;
	for(int i=1;i<=n;i++){
		if(A[i]>0) add(S,i,A[i]),tot+=A[i];
		else if(A[i]<0) add(i,T,-A[i]);
	}

	add(t,s,INF);

	if(dinic()<tot)cout<<"No Solution"<<endl;
	else {
		int res=f[idx-1];//首先看t->s的边的容量
		S=t,T=s;
		f[idx-1]=f[idx-2]=0;//删去t->s的边的容量
		cout<<res-dinic()<<endl; 
	}
}

signed main(){
	ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);
	int T=1;
	while(T--) slove();
}