【吴恩达深度学习】L1W2 学习笔记
第二周:神经网络的编程基础
2.1 二分类(Binary Classification)
传播算法和反向传播
https://zhuanlan.zhihu.com/p/71892752
https://aistudio.baidu.com/aistudio/projectdetail/1601963

符号定义 :
\(x\):表示一个\(n_x\)维数据,为输入数据,维度为\((n_x,1)\);
\(y\):表示输出结果,取值为\((0,1)\);
\((x^{(i)},y^{(i)})\):表示第\(i\)组数据,可能是训练数据,也可能是测试数据
\(X=[x^{(1)},x^{(2)},...,x^{(m)}]\):表示所有的训练数据集的输入值,放在一个 \(n_x×m\)的矩阵中,其中\(m\)表示样本数目;
\(Y=[y^{(1)},y^{(2)},...,y^{(m)}]\):对应表示所有训练数据集的输出值,维度为\(1×m\)。
用一对\((x,y)\)来表示一个单独的样本,\(x\)代表\(n_x\)维的特征向量,\(y\) 表示标签(输出结果)只能为0或1。 而训练集将由\(m\)个训练样本组成,其中\((x^{(1)},y^{(1)})\)表示第一个样本的输入和输出,\((x^{(2)},y^{(2)})\)表示第二个样本的输入和输出,直到最后一个样本\((x^{(m)},y^{(m)})\),然后所有的这些一起表示整个训练集。
在实现神经网络的时候,将\(X^{(i)}\)按照列来堆叠组成一个矩阵\(X\)(像上图那样)会使训练更有效率。
2.2 逻辑回归(Logistic Regression)
我们会考虑将\((y- \hat{y})^2\)也就是误差的真实值只差,但这样的话对于不同的预测值,其误差可能会相差很大,这时候我们可以考虑将其归一化,也就是都化为一个区间。你想让\(\hat{y}\)表示实际值\(y\)等于1的机率的话,\(\hat{y}\) 应该在0到1之间。因此在逻辑回归中,我们的输出应该是\(\hat{y}\)等于由上面得到的线性函数式子作为自变量的sigmoid函数中
https://blog.csdn.net/weixin_41334453/article/details/102805479
2.3 逻辑回归的代价函数(Logistic Regression Cost Function)

为了训练逻辑回归模型的参数参数\(w\)和参数\(b\),我们需要一个代价函数,通过训练代价函数来得到参数\(w\)和参数\(b\)。
损失函数:
损失函数又叫做误差函数,用来衡量算法的运行情况,Loss function:\(L\left( \hat{y},y \right)\).
我们通过这个\(L\)称为的损失函数,来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半,但是通常在逻辑回归中我们不这么做,因为当我们在学习逻辑回归参数的时候,会发现我们的优化目标不是凸优化,只能找到多个局部最优值,梯度下降法很可能找不到全局最优值,虽然平方差是一个不错的损失函数,但是我们在逻辑回归模型中会定义另外一个损失函数。
在逻辑回归中用到的损失函数是:\(L\left( \hat{y},y \right)=-y\log(\hat{y})-(1-y)\log (1-\hat{y})\)

代价函数
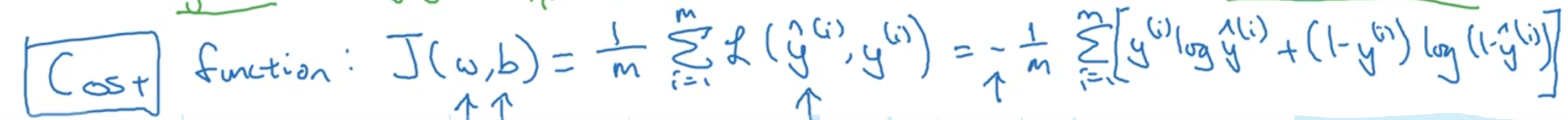
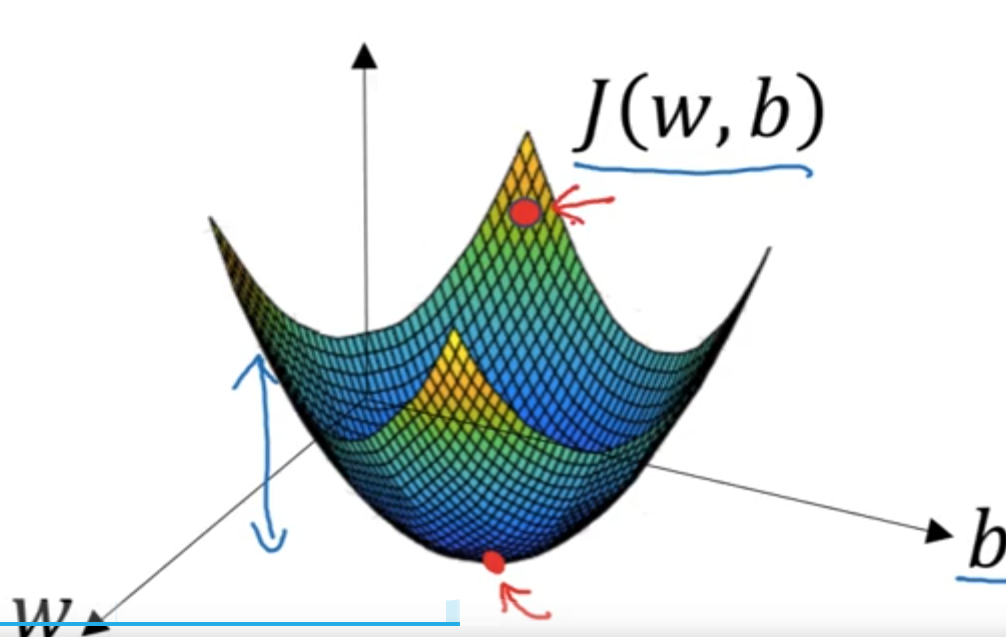
2.4 梯度下降法(Gradient Descent)
-
初始化\(w\)和\(b\)(赋初值)
-
求损失函数
-
想着梯度方向(下降最快方向)来更新\(w\)和\(b\),并不断迭代
-
在一定迭代次数或者损失达到一定标准后停止迭代

\(:=\)表示更新参数,
$a $ 表示学习率(learning rate),用来控制步长(step),即向下走一步的长度\(\frac{dJ(w)}{dw}\) 就是函数\(J(w)\)对\(w\) 求导(derivative)
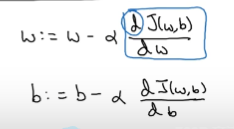
\(\frac{\partial J(w,b)}{\partial w}\) 就是函数\(J(w,b)\) 对\(w\) 求偏导,使用\(dw\) 表示这个结果
\(\frac{\partial J(w,b)}{\partial b}\) 就是函数\(J(w,b)\)对\(b\) 求偏导,使用\(db\) 表示这个结果
为什么不用均方误差来表示线性函数的损失函数
https://blog.csdn.net/lafengxiaoyu/article/details/109916750


 浙公网安备 33010602011771号
浙公网安备 33010602011771号